自组建激光干涉仪测量平行板楔角
从守民,路洪艳,刘保通
(淮北师范大学 物理与电子信息学院,安徽 淮北235000)
1 引 言
随着科学技术的迅猛发展,在工业生产和科学实验中,经常会遇到测量微小角度的问题.文献[1-2]分别介绍了利用准直管测定玻璃基板两平面存在的微小角度、利用测角仪测量微小角度、利用分光计和移测显微镜来测量楔角的多种方法.但是在楔角非常微小的情况下(如楔角的数量级为秒),上述诸多方法有的无法测量,有的精度达不到要求.鉴于此,我们用自组建的激光干涉仪来测量平行板的微小楔角.这种方法操作简单、灵敏度高,并且可达到0.1″的精度.
2 实验装置与原理
如图1所示,两相干点光源在空间满足光程差等于常量的点的轨迹是以S1S2连线为轴线的双叶旋转双曲面,垂直于S1S2连线放置一观察屏[3],在屏上呈现出同心环状的非定域干涉条纹.

图1 两点光源的非定域干涉图样
在光学实验平台上组建成如图2所示的激光干涉仪.图中A为激光器,L为凸透镜,F为带有小孔的白屏,P为待测楔角的透明平板.平行激光束经过凸透镜会聚后成为发散的球面波,该球面波照射到平板上并让平板的法线与光束的光轴重合.由平板的前后两表面反射回来的两球面波在反射光所在的空间叠加,形成两点光源的非定域干涉.在透镜的会聚点处垂直于光束的光轴放置带有小圆孔的屏,并让透镜的会聚点与小圆孔重合,在屏上将会出现1组同心环状的干涉条纹.当被测平板的两表面严格平行时,则同心环状的干涉环的中心与小圆孔的中心完全重合;当平板的两表面有一微小楔角时,同心干涉环的中心相对小圆孔的中心就有一定的偏离,根据偏离的大小和其他有关参量就可以计算出楔角的大小.

图2 激光干涉仪示意图
如图3所示,S为透镜会聚点即球面波的中心(也是小圆孔的中心),由该点发出的球面波经平板前后两表面反射后分别成像于S1和S2,反射波相当于从S1和S2两点发出,它们是相干光源,在小孔屏上形成同心环状的非定域干涉条纹,条纹的中心在S1和S2的连线上的O点,离点光源S即小圆孔中心的距离为l.设平板的楔角为α,折射率为n,厚度为t,板的前表面距小孔屏的距离为D.由几何光学知识可知:

图3 实际测量原理图

在n D≫t的情况下,有
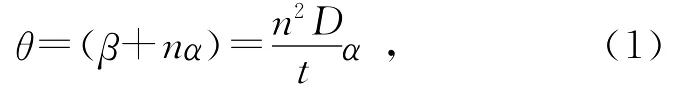
因而得到

或表示为

由(1)式可知,干涉环的中心相对于屏上圆孔中心的偏角θ与平板的楔角α成正比,此装置可视为对α角的放大器,n2D/t可视为角放大系数.在实际操作时角放大系数可以很大.例如D=1 m,t=2.25 mm,n=1.5,n2D/t可达到103.若α=5×10-6rad(约1″)则有l=10 mm.由此可见,即使对只有秒级楔角的平板,这种方法也能有明显的效果.如果偏离量l可测准到1 mm,则可测出0.1″楔角.此外,还可由条纹中心偏离的方向来判断α角的倾斜方位.
3 实验测量
实际测量装置如图4所示.用He-Ne激光器做光源对迈克耳孙干涉仪上的补偿板进行了测量.参数如下:厚度t=8 mm;折射率n=1.515;D=900 mm.测出条纹中心偏离圆孔中心的距离l=2.6 mm,由此算出α=5.6×10-6rad.

图4 实际测量装置图
4 结束语
自组建激光干涉仪测量平行楔角的方法有以下优点:a.操作简单、灵敏度高、测量精度高;b.不仅能判断楔角的倾斜方位,还能根据条纹的规则程度判断平板的平面平整度和折射率的均匀程度,如表面不太平整或折射率不是很均匀,则条纹会有一定程度的畸变或缺陷;c.可作为非定域干涉的演示实验,对学生理解干涉现象有较好的帮助;d.可作为物理学专业学生的设计性实验[4],既能使学生综合利用所学的几何光学和波动光学的知识来推导测量公式[5],又能让学生自己动手组建干涉仪来实际操作,这样可以提高学生的学习兴趣和积极性,有利于学生综合能力的培养.
[1] 李相宇,贺莉清,邵阴梅,等.小工件平行度垂直测量新方法及精度分析[J].光学仪器,1998,20(4):8-11.
[2] 张雄.菲涅尔双棱镜折射率和锐角的测量[J].物理实验,1996,16(4):146-147.
[3] 姚启钧.光学教程[M].4版.北京:高等教育出版社,2008:16.
[4] 林仁荣.用激光干涉法测量电致伸缩系数[J].物理实验,2009,29(6):5-6.
[5] 从守民,袁广宇,杨保华.在分光计上做双棱镜干涉实验[J].物理实验,2008,28(12):36-37.

