受限系统中电磁诱导吸收条件下的光子带隙

卢一鑫，杨璐娜

（1．西安文理学院 物理学与光电工程系，陕西 西安710065；2．西北大学 物理系，陕西 西安710069）

1 引 言

原子相干效应是光与原子相互作用的一种重要物理现象，近年来备受关注．它在原子冷却、测磁学、增强原子色散、原子量子态的相干布居传输、光速减慢及增强、原子纠缠的产生以及量子开关等方面有重要的应用价值．原子相干产生了许多新的效应，如电磁诱导透明（electromagnetically induced transparency，简称 EIT）［1－3］和电磁诱导吸收（electromagnetically induced absorption，简称EIA）［4－5］．EIA 是基于原子相干对吸收的相长干涉．Akulshin等［4］首先在铷原子气室中观察到了EIA现象，同时进行了相应的理论研究，并提出了实现EIA必须满足的3个基本条件［5］：1）Fe＝Fg＋1，其中Fg和Fe分别为基态和激发态的总角动量；2）基态Fg到激发态Fe的跃迁是封闭的循环跃迁；3）基态必须是简并的，即Fg≥1，在零磁场情况下有2Fg＋1个简并的Zeeman子能级．近期的实验研究发现相位共轭四波混频技术中，当原子从EIT（暗态）转化为EIA（明态）时也可得到增强的四波混频信号．理论分析表明，对应于EIA系统可产生周期性调节的光子带隙结构，使介质的折射率发生周期性变化，某些频率的光子会被禁止在介质中传播，从而形成类似于晶体中电子能级禁带的光子带隙［6－7］，形成特定的光子带隙结构可以对入射光产生明显的反射［8］．

本文基于Y型四能级系统，铷原子在量子调控作用下处于EIA（电磁诱导吸收）即明态条件下观察四波混频（FWM）信号增强的现象，研究光子带隙结构的变化规律．

2 理 论

Y型四能级系统如图1所示．

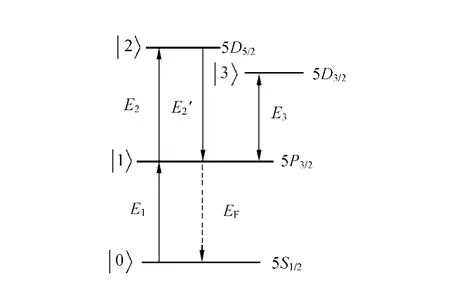
图1 Y型四能级系统

一般而言FWM信号ρ（3）10可以通过半经典的方法进行求解耦合的密度矩阵方程而得到，当E3固定且其缀饰效应可以不计，可以利用微扰链方法直接得到ρ（3）10的表达式：

对于FWM过程可以得到

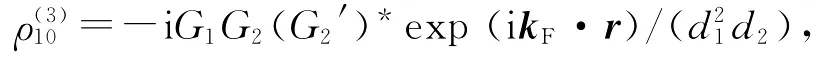
式中d1＝Γ10＋iΔ1，d2＝Γ20＋i（Δ1＋Δ2）．

考虑E3的缀饰效应，这时原子处于多缀饰状态，利用微扰链方法可以得到下列耦合方程：

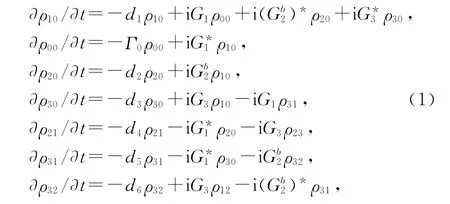
其中Gb2＝G2＋G2′，d3＝Γ30＋i（Δ1＋Δ3），d4＝

Γ21＋iΔ2，d5＝Γ31＋iΔ3，d6＝Γ32＋i（Δ3－Δ2）．Gi是拉比频率．解此多缀饰耦合方程可以得到：

在相互作用表象下，Y四能级原子的哈密顿量可以写成：

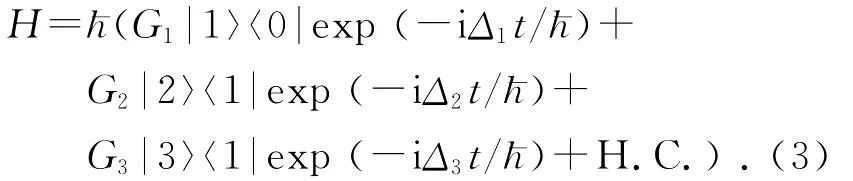
而系统的波函数可以展开成：

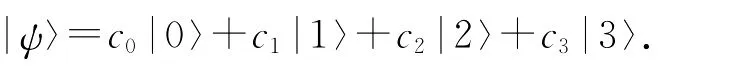
根据H｜ψ〉＝E｜ψ〉可以求出系统明态表示：

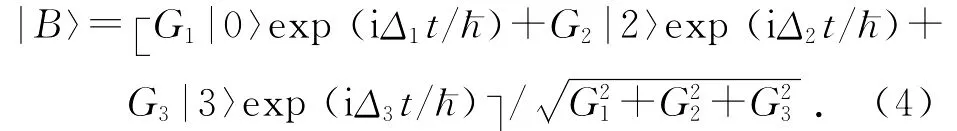
这时可以得到原子在明态｜B〉上的分布：

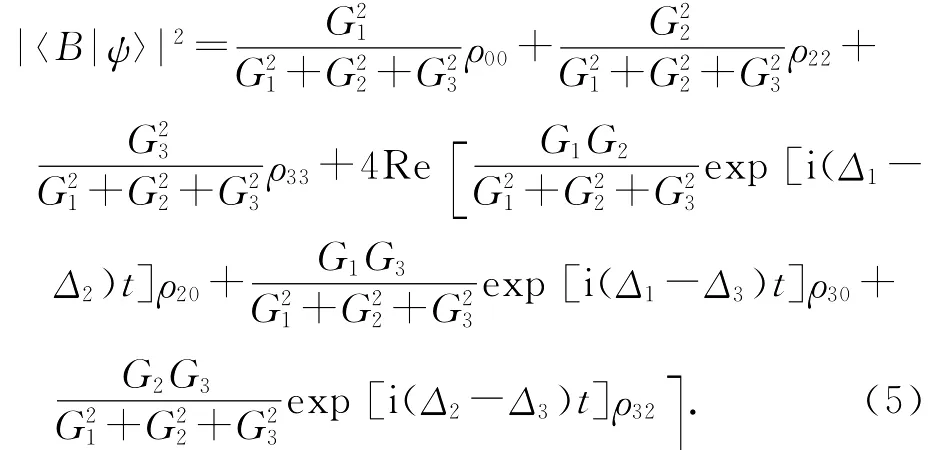
假设

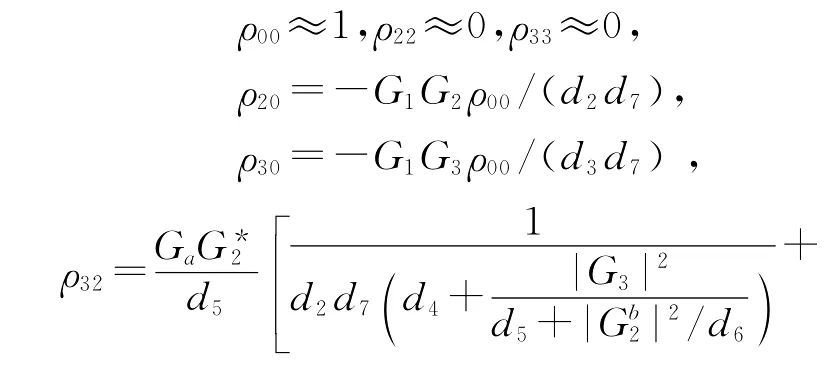
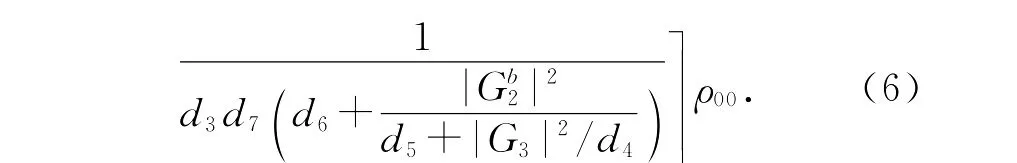
d5＝i（－Δ2＋Δ3）＋Γ32，d6＝iΔ3＋Γ31，d7＝d1＋．因此考虑在明态｜B〉中的三基态｜0〉，｜2〉和｜3〉之间的干涉．FWM 信号的强度可写成：，其中N′＝N｜〈B｜ψ〉｜2则决定光子带隙的演化．

3 实验装置和实验方法

实验装置：实验系统可以完成包括单光子、双光子AS和SR光谱、双缀饰EIA及FWM的实验．以87Rb中一Y系统为例，它的各个能级分别由5S1／2（F＝2），5P3／2，5D3／2及 5D5／2组成（见图1）．可以采用图2所示的实验方案［6］：参考样室C1，C2，C3皆为2 cm厚的宏观样室，分别用作监测λ1，λ2及λ3的调谐量．第4个样室为ETC，通过光束的不同配置和挡光用作测量单光子及双光子过程的AS和SR光谱、双缀饰EIT、FWM及SDWM信号．实验中水平偏振的探测场来自于波长为780 nm的外腔式二极管激光器（ECDL），垂直偏振的耦合场E2和E2′及泵浦场E3和E3′分别由波长为775．98 nm的Ti∶Sapphire激光器和波长为776．16 nm的另一外腔式二极管激光器（ECDL）产生．780 nm波长激光器探测光频率的扫描采用调整光栅的角度和电流大小实现．D6用于探测四波混频信号（其中包含少量的六波混频信号），其相位匹配条件为kF＝k1＋k2－k2′，kF＝k1＋k3－k3′．通过调节泵浦激光束的空间配置来优化选择不同的相位匹配条件（即优化选择它们的不同相干长度），使其中1个FWM（kF＝k1＋k2－k2′）占绝对优势，将剩下的混频信号被抑制或减弱．

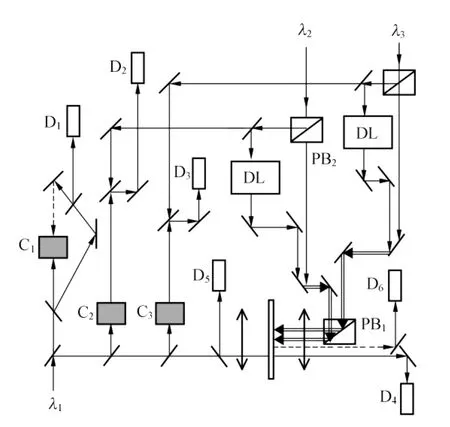
图2 ETC实验光路图

光路图元件：C1，C2，C3是2 cm厚铷泡的宏观样室；ETC为铷泡的超薄样室；D1～D5为光电探测器，分别接收单光子及双光子过程的AS和SR、双缀饰EIT、FWM 及SDWM 信号；PB1，PB2是分光棱镜；DL是激光器；其余都是全反射镜．

实验方法：光束的几何配置和原子的能级结构如图3～6所示，缀饰场E1和E1′为TM模式，它们之间有微小的夹角θ1；缀饰场E2和E2′为TE模式，它们之间也有微小的夹角θ2．它们入射到原子介质中以后，分别通过相互干涉在特定方向上形成了2个驻波场，这2个驻波场通过原子相干和交叉Kerr效应诱导出了2个取向不同的一阶极化率和非线性折射率空间周期性变化的光栅，从而形成光子带隙．根据具体的一阶极化率和非线性折射率的空间周期性变化规律，运用数值方法计算出相应的光子带隙结构．

探测光按照图中的E3方向入射，光子带隙可以对其进行反射，从而产生四波混频信号EF1和EF2．并且我们发现当改变探测光相对光栅的入射角度α时，仍然可以对其进行有效地反射，这说明了全向反射的存在性．由于周期性结构的存在，产生后的混频信号在传播过程中会形成偶极、带隙、离散等类型的光孤子．并且由于2个光栅的取向不同，探测光和混频光在其中的传播模式也不同（图5和图6），因此探测光的反射以及混频光形成孤子的特征也存在很大差异．

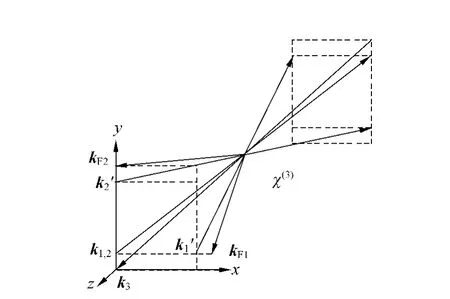
图3 光束几何配置图

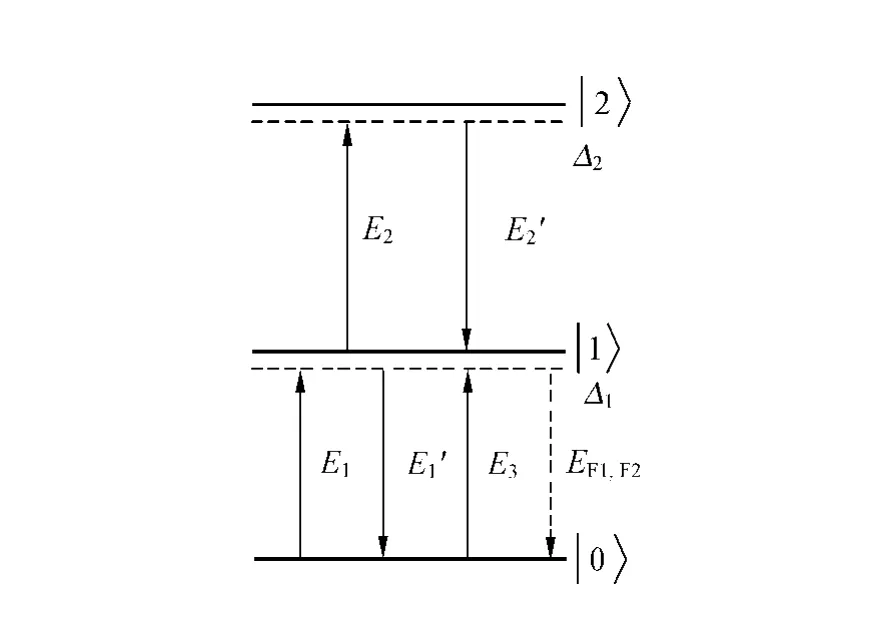
图4 原子能级图

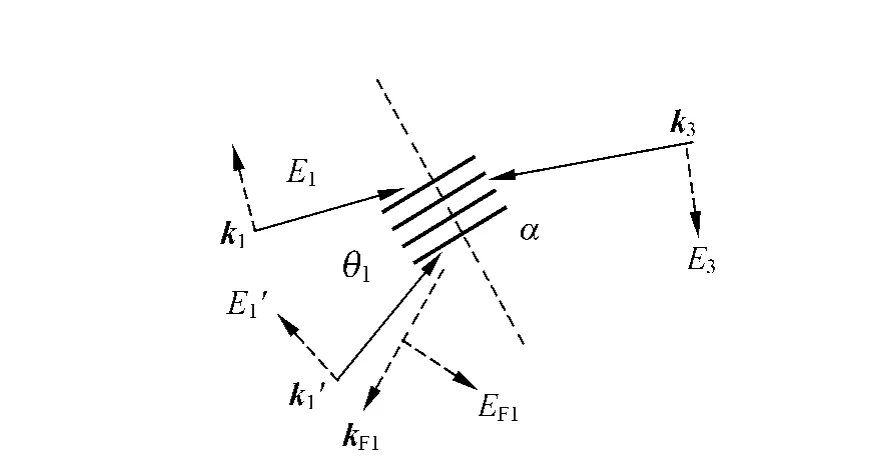
图5 光束E 1，E 1′，E 3 产生四波混频信号E F1的几何配置及模式图

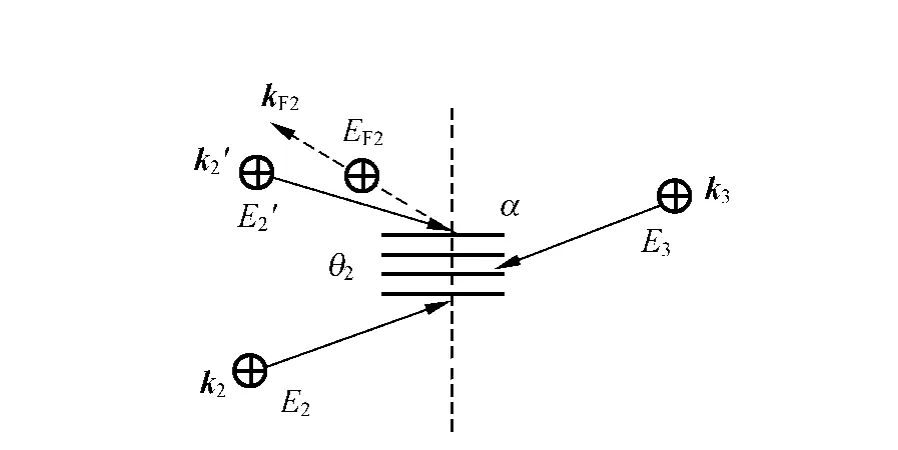
图6 光束E 2，E 2′，E 3 产生四波混频信号E F2的几何配置及模式图

3 实验结果

由于探测场在E2和E2′与E1和E1′形成的光栅中的模式不同，对这2对驻波场诱导出不同的光子带隙分别进行研究，其中改变探测光的入射角度可以有效改变这2种光子带隙的宽度，具体结果如图7所示，图7中四波混频信号EF1为E3在光子晶体以TM模传播时产生，EF2为E3在光子晶体以TE模传播时产生．同时，调节缀饰场的失谐量，使系统中产生EIA现象，在此条件下，光子晶体对探测光产生很强的反射，四波混频和六波混频信号得到增强．

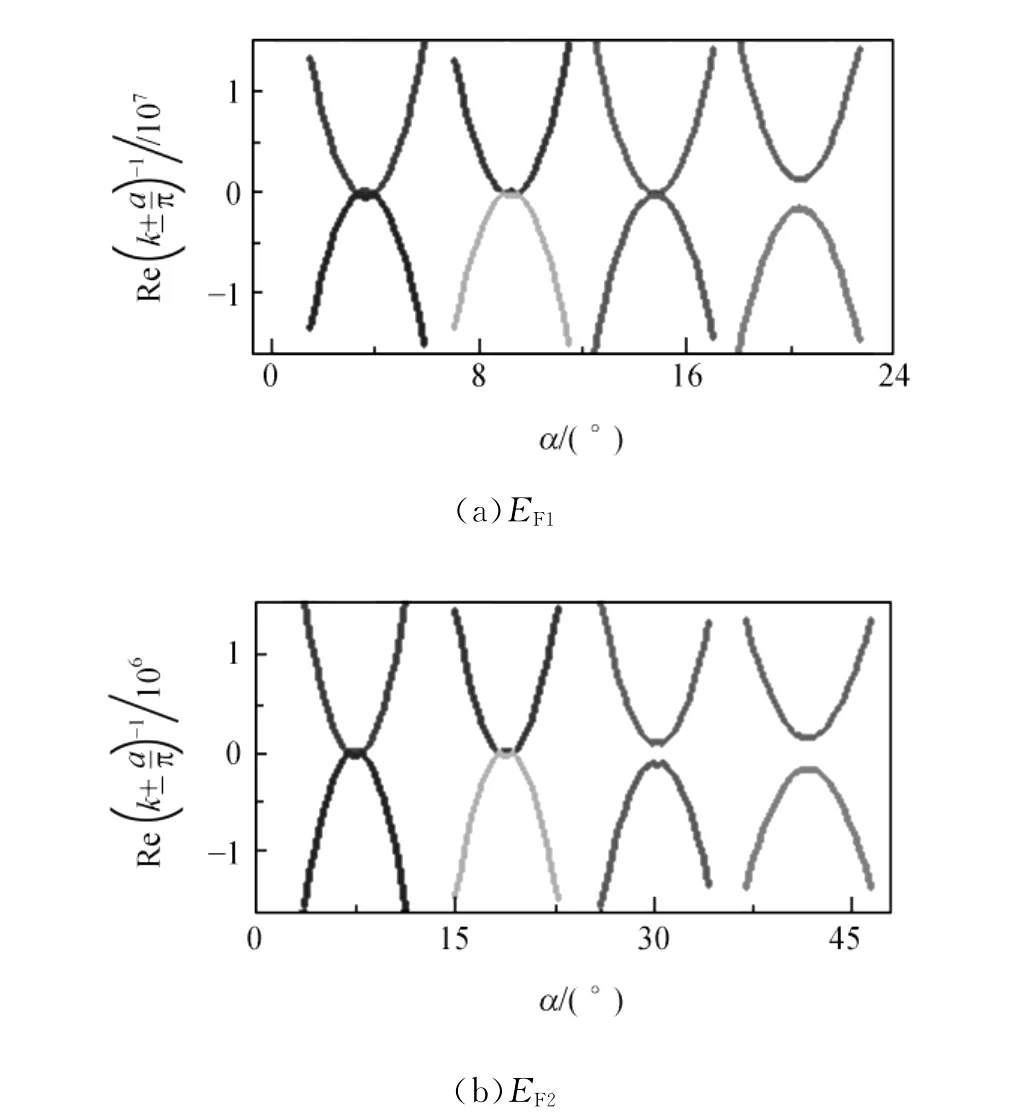
图7 不同光子带隙与探测光E F1′的入射角度之间的关系

4 结束语

通过实验，初步得到关于EIA条件下光子带隙变化的规律：对于入射角度不同的探测光，其在TM模传播时，光子带隙的宽度比在TE模传播时增加得更迅速．这为进一步了解光子带隙基本的结构和变化提供了一些帮助．

［1］ Harris S E．Electromagnetically induced transparency［J］．Phys．Today，1997，50（7）：36－42．

［2］ Marangos J P．Electromagnetically induced transparency［J］．J．Mod．Opt．，1998，45（3）：471－503．

［3］ Wu Ying，Yang Xiao－xue．Electromagnetically induced transparency in V－，Λ－，and cascade－type schemes beyond steady－state analysis ［J］．Phys．Rev．A，2005，71（5）：053806．

［4］ Akulshin A M，Barreiro S，Lezama A．Electromagnetically induced absorption and transparency due to resonant two－field excitation of quasidegenerate levels in Rb vapor［J］．Phys．Rev．A，1998，57（4）：2996－3002．

［5］ Lezama A，Barreiro S，Akulshin A M．Electromagnetically induced absorption［J］．Phys．Rev．A，1999，59（6）：4732－4735．

［6］ Li DW，Zhang L，Zhou Z C，et al．Electromagnetically induced photonic bandgap in hot Cs atoms［J］．J．Opt．Soc．Am．B，2010，27（4）：690－695．

［7］ Wu J H，Artoni M，La Rocca G C．Controlling the photonic band structure of optically driven cold atoms［J］．J．Opt．Soc．Am．B，2008，25（11）：1840－1849．

［8］ Brown A W，Xiao M．All－optical switching and routing based on an electromagnetically induced absorption grating ［J］．Opt．Lett．，2005，30（7）：699－701．