SGP4/SDP4模型预报可靠性分析*

刘 卫，缪元兴

(中国科学院国家天文台云南天文台，云南 昆明 650011)

TLE是北美防空联合司令部(NORAD)发布的空间在轨飞行物的轨道根数，它通过特定方法移除周期变化得到平根数。为得到更好的预报精度，TLE必须配合NORAD开发的SGP/SDP模型使用，精确地重建移除的周期变化部分。按照NORAD标准所有空间目标被分为:近地(周期≤225 min)、深空(周期 ＞225 min)。NORAD共发布了 SGP、SGP4、SGP8、SDP4、SDP85个预报模型，其中SGP、SGP4、SGP8适用于近地目标，SDP4、SDP8适用于深空目标。目前NORAD发布的TLE根数是与 SGP4/SDP4 兼容的［1］。

美国全球观测网(SSN)的观测资料生成了全球最大的空间目标编目数据库，并以TLE根数形式发布出来，被广泛使用。对于SGP4/SDP4的定轨精度，文献［2－3］分别就2006版、1980版作过较详尽的分析，但其中也存在几个问题主要是所选参考轨道精度。本文利用激光测距资料定出精度达厘米级的轨道作为参考轨道，给出两种典型版本SGP4/SDP4的定轨精度及外推误差随时间的变化。分析得出不同高度轨道用SGP4/SDP4模型外推的可靠圈数，为工程计算提供了一定的依据。

1 参考轨道计算

在ILRS网站下载相应卫星对应时间段的激光测距资料并转化成相应格式，下载CPF格式的预报资料内插得到TLE对应时间的初始根数，用精密定轨软件结合SLR资料定出对应时间段的精密轨道(参考轨道)并以离散的形式给出星历［4］。目前的激光测距资料精度在3 cm以内，在实际定轨中，3 d弧段内SLR资料较多的卫星，定轨RMS可达厘米级。对某些SLR资料较少的弧段，定轨RMS要稍差为米级。本文中算例均选用观测资料较多的弧段。

精密定轨模型:(1)70×70阶地球引力场模型GGM01C;(2)30×30阶TOPEX 4.0海潮模型;(3)大气密度 DTM－78模型，其中的F10.7太阳辐射流量及地磁活动指数 Kp采用NOAA’s National Geophysical Data Center提供的实测值;(4)极移、UTI－UTC采用IERS B公报，岁差、章动、恒星时计算及天文常数系统采用IERS Conventions(2003)［5］;(5)N体摄动中摄动天体星历采用DE405历表;(6)数值积分:KSG积分器;(7)太阳光压，固体潮摄动。

表1 数值试验中采用的激光卫星Table 1 Satellites with SLR data used in our numerical experiments

2 SGP4/SDP4预报模型

自SGP/SDP模型［6］公布以来，不断发展出现了很多版本的代码，比较典型的有DOD、GSFC、AFSPC等，Vallado D A等人对几种典型的代码进行了总结，并对时间坐标系统进行了说明［1］。

2.1 TLE中的时间系统与坐标系统

TLE采用的时间系统为UTC，而坐标系统为瞬时真赤道平春分点(TEME of Date)，TEME of Date与J2000的坐标转换如下［7］:

其中Δμ为赤经章动;(PR)、(NR)为岁差、章动矩阵。转换中采用IAU提供的转化程序［5］。

2.2 从平根数到瞬时根数

2.3 预报

采用的SGP4/SDP4模型1980版为文［6］中Fortran代码，2006版为(AFSPC)发布的C语言代码。两个版本的主要区别:合并了SGP4/SDP4中的公用部分以简化代码，变量全部用双精度，并更新了天文常数系统;改进了Kepler方程的解法，更新了日月周期摄动的应用及初始化问题［1］(这对中高轨卫星两种版本有较大差异，由图4、5可以看出)。预报过程中从TLE历元起每隔360 min给出一组轨道状态量(位置、速度)。

3 预报误差分析

由精密定轨软件给出与预报相同历元的一系列参考星历，并将预报星历与参考星历转换到同一坐标系(J2000)下，预报误差定义如式:Δr=|rprediction－rrefer|。根据不同轨道高度的预报误差变化趋势，分别作出了15、30、60、120 d的预报误差变化图(图1～4)，(图中V1980、V2006分别代表1980版本2006版本代码计算结果)。

图1 近地预报15天误差变化图Fig.1 Variations of errors from prediction within 15 days of near－earth orbits

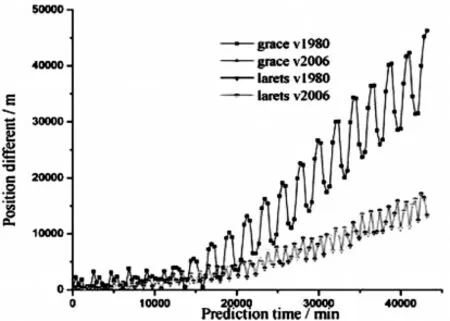
图2 低轨预报30天误差变化图Fig.2 Variations of errors from prediction within 30 days of low－earth orbits

图3 预报60天误差变化图Fig.3 Variations of errors from prediction within 60 days of low－earth orbits

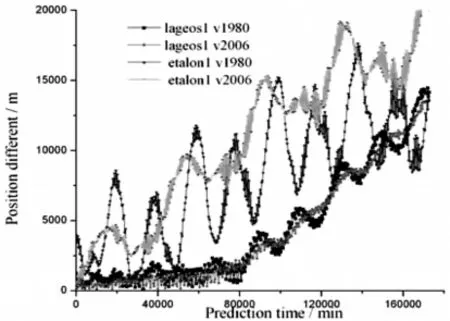
图4 高轨预报120天误差变化图Fig.4 Variations of errors from prediction within 120 days of high－earth and semi－synchronous orbits

从图中可以看出GOCE预报3 d左右误差开始显著增长，ANDEC预报7 d左右误差开始显著增长，GRACE－A、Larets、ERS－2 预报10 d 左右误差开始显著增长，Ajisai、LAGEOS－1预报30 d左右误差开始显著增长，Etalon－1、COMPASS－M1预报20 d左右误差开始显著增长，ETS－8同步卫星误差波动较大，预报10 d左右误差开始显著增长。

4 结论

对LEO(h≤2000 km)卫星，V2006与V1980差别不大，定轨精度均在几百米量级，轨道高度越低定轨精度越差，预报可靠的时间段越短，这与［2］的结论是一致的。对MEO(h≥5000 km)［8］V2006与 V1980有较大差异，V1980预报误差表现出较大的振荡。综合以上，对V2006版SGP4/SDP4预报模型得出结论见表2。

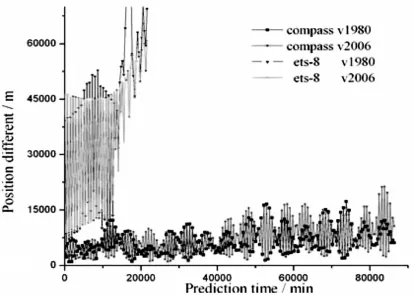
图5 半同步同步预报60天误差变化图Fig.5 Variations of errors from prediction within 60 days of semi－synchronous and geosynchronous orbits

表2 SGP4/SDP4预报误差结论Table 2 Conclusion about the errors of the SGP4/SDP4 predictions

［1］Vallado D A，Crawford P，Hujsak R，et al.Revisiting Spacetrack Report#3 ［J］.AIAA，2006－6753.

［2］韦栋，赵长印，SGP4/SDP4模型精度分析 ［J］.天文学报，2009，50(3):333－339.Wei Dong，Zhao Changyin.Analysis on the Accuracy of the SGP4/SDP4 Model［J］.Acta Astronomica Sinica，2009，50(3):333－339.

［3］韩蕾，陈磊，周伯昭.SGP4/SDP4模型用于空间碎片轨道预测的精度分析 ［J］.中国空间科学技术，2004(4):65.Han Lei，Chen Lei，Zhou Bozhao.Precision Analysis of SGP4/SDP4 Implemented in Space Debris Orbit Prediction［J］.Chinese Space Science and Technology，2004(4):65.

［4］刘卫，缪元兴.采用重置参数的轨道改进算法 ［J］.天文研究与技术——国家天文台台刊，2010，7(4):318－324.Liu Wei，Miao Yuanxing.An Improved Method of Precise Orbit Determination by Resetting Model Parameters ［J］.Astronomical Research ＆ Technology——Publications of National Astronomical Observatories of China，2010，7(4):318－324.

［5］McCarthy D D，Petit G.IERS Conventions(2003).(IERS Technical Note;32)Frankfurt am Main:Verlag des Bundesamts für Kartographie und Geodäsie，2004:43 －100.

［6］Hoots F R，Roehrich R L.Spacetrack Report NO.3 ［R］.NORAD，1980.

［7］李济生.人造卫星精密轨道确定 ［M］.北京:解放军出版社，1995:84－187.

［8］刘林，胡松杰，王歆.航天动力学引论 ［M］.南京:南京大学出版社，2006:176.