单体1∶1∶6方形截面建筑绕流的大涡模拟

郑德乾，顾 明，张爱社，张建国

(同济大学 土木工程防灾国家重点实验室，上海 200092)

单体1∶1∶6方形截面建筑绕流的大涡模拟

郑德乾，顾 明，张爱社，张建国

(同济大学 土木工程防灾国家重点实验室，上海 200092)

基于Fluent 6软件平台，采用大涡模拟(LES)方法对一宽高比为1:1:6的高层建筑缩尺模型表面的平均和脉动风压进行了数值模拟，并与相应风洞试验结果进行了比较和分析，然后，研究了不同来流湍流度对结构表面风压分布的影响。结果表明:(1)对于类似研究的0°风向角下的方形截面建筑来说，结构迎风面风压直接受来流湍流的影响;侧面由于存在流动分离，其风压主要受分离产生的特征湍流的影响，受来流湍流度的影响较小;而背风面处于复杂的尾流区，其表面风压受到的影响因素比较复杂。(2)在风压系数的统计特性和自谱上，LES结果与风洞试验结果均能够基本保持一致，LES方法能够较准确预测结构表面的平均和脉动风压分布。

高层建筑;大涡模拟;风洞试验;平均风压系数;脉动风压系数

目前，在实际工程结构抗风研究中，除了风洞试验这一传统手段之外，随着计算机技术和湍流模型的发展，CFD数值模拟已经越来越有可能应用于建筑结构风荷载研究中［1－9］。运用计算流体动力学(CFD)技术进行结构风荷载的数值模拟是结构抗风研究极具前景的途径。

与传统的风洞试验相比，数值模拟具有成本低、不受模型尺度的影响、可以方便地研究不同参数的影响等优点。以往的CFD数值模拟计算大都采用基于时间平均的雷诺平均数值模拟(RANS)，主要用于模拟湍流的平均运动，无法模拟湍流的小尺度的瞬时运动。随着计算机软硬件技术的迅速提高，大涡模拟(Large Eddy Simulation，简称为LES)方法逐渐得到了应用，该方法基于空间平均，把湍流中的大涡和小涡分开处理，将大尺度的涡直接求解，而将小尺度涡运用模型来反映，因此对流场的脉动信息模拟的更好。文献［6－8］分别对CAARC高层建筑标准模型、宽高比1∶1∶4和1∶1∶2的建筑进行了LES数值模拟，并与相应风洞试验结果进行了比较;文献［9］则对一立方体建筑进行了风洞试验和LES数值模拟。

本文首先对一宽高比为1∶1∶6的单体方形截面高层建筑进行了刚性模型风洞测压试验，获得了其表面的平均和脉动风压分布。然后，基于Fluent 6软件平台，采用大涡模拟(LES)方法对该方形截面高层建筑缩尺模型表面的平均和脉动风压进行了数值模拟，并与相应风洞试验结果进行了比较和分析，以验证和探讨本文方法的有效性和适用性。最后，研究了不同来流湍流度对结构表面风压系数的影响。

1 风洞试验

某高层建筑宽高比 B∶D∶H=1∶1∶6，如图 1(a)所示，其刚性模型同步测压风洞试验在同济大学土木工程防灾国家重点实验室风洞试验室的TJ－2大气边界层风洞中进行，模型缩尺比为1:500，缩尺模型边长D=0.1 m。按照研究对象所处地面粗糙度类别，试验中按照1/500的缩尺比模拟了B类风场，试验测得的平均风剖面和湍流度剖面分别如图1(b)、图1(c)所示。试验时将模型放置在转盘中心，通过旋转转盘模拟不同风向角。限于篇幅，本文主要对图1(a)所示的0°风向角进行了数值模拟计算。风洞试验中一共布置了200个测点，这里仅给出了用于本文数值模拟和风洞试验比较的模型表面主要测点布置，如图1(a)所示。此外，本文仅给出主要的试验结果(见后)，用于和数值模拟结果比较。

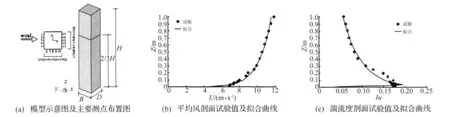
图1 测点布置图、风洞试验平均风剖面和湍流度剖面Fig.1 Sketch of model，measuring point position，mean wind velocity and turbulent intensity profiles of wind tunnel test

2 数值模拟方法

为了和试验结果比较，本文在对宽高比1:1:6方形截面高层建筑的大涡模拟计算中建立了与风洞试验相同缩尺比(1:500)的缩尺模型。以下是大涡模拟方法的基本控制方程和本文数值计算中的参数设置。

2.1 控制方程

CFD数值模拟中，钝体绕流问题的控制方程是粘性不可压连续方程和Navier-Stokes方程，基于空间平均的LES模型控制方程可表示为:

2.2 基本参数

计算流域取为94D×28D×18D(流向x×展向y×竖向z)，如图2(a)所示。网格剖分采用区域分块非均匀结构化网格，壁面附近区域网格加密，最小网格尺度为3D/5000，远离壁面处网格逐渐稀疏，如图2(b)所示。基于此网格布置计算得到的壁面Y+值分布如图2(c)所示，由图可见壁面Y+值均小于3.5，满足Y+＜5的要求。

首先采用基于RANS的Realizable k－ε湍流模型配合壁面函数进行方柱的定常绕流数值模拟计算，然后，将计算收敛后的流场作为LES计算的初始流场进行方柱的非定常绕流数值模拟计算。

采用速度入口边界条件，进流面边界条件尽量与模型风洞试验相一致，以便数值模拟结果和试验结果的对比，使用对数律拟合了风洞试验的平均风剖面［图1(b)］和湍流度剖面［图1(c)］

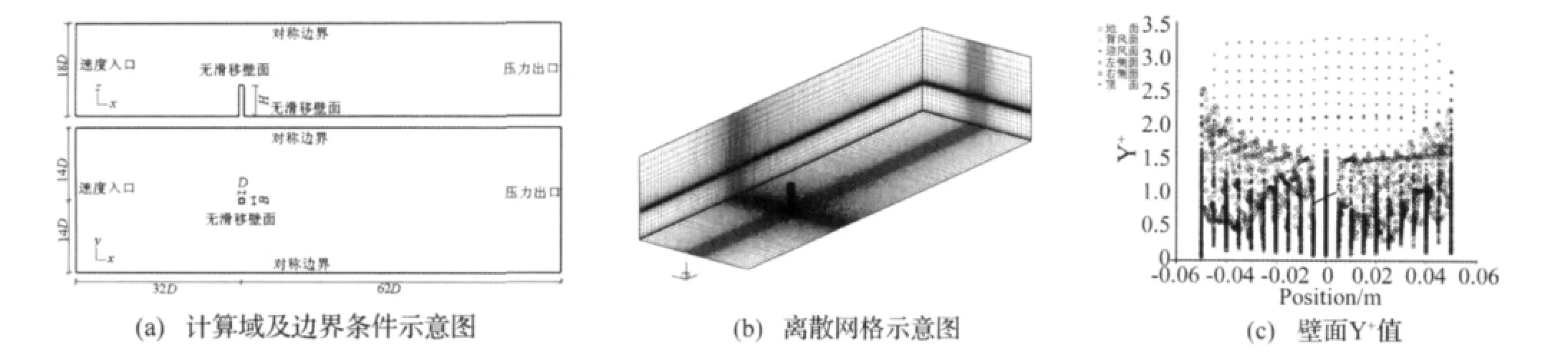
图2 计算域、边界条件、网格示意图和壁面Y+值图Fig.2 Sketch of calculation domain，boundary conditions，mesh scheme and value of wall Y+

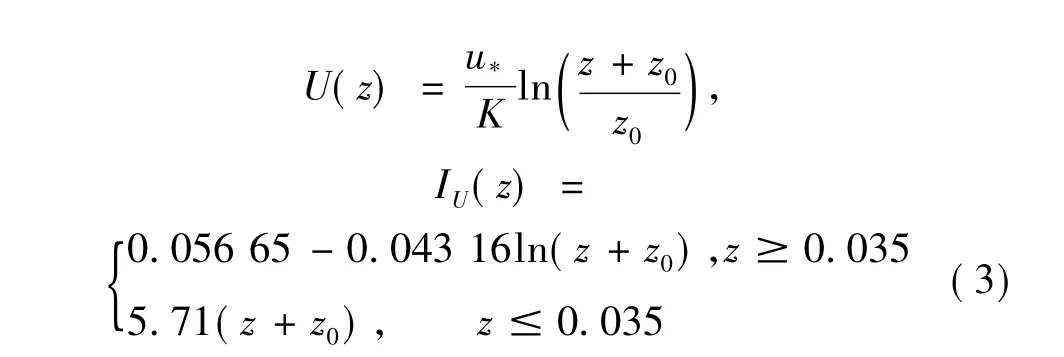
式中冯·卡门常数K=0.42，粗糙长度 z0=2.25×10－4m，摩擦速度u*=0.577 m/s;湍动能k(z)和湍动能耗散率ε(z)为:

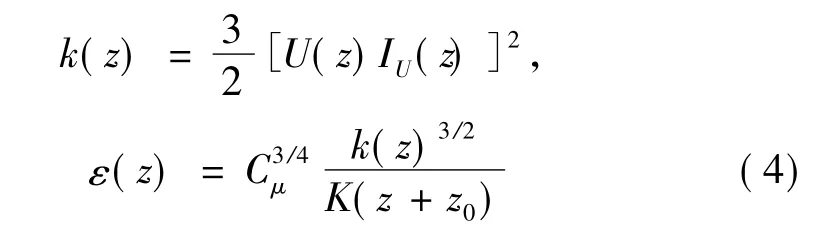
式中Cμ为模型常数，取为0.09;通过UDF(User Defined Function)编程将上述入流边界条件与Fluent连接。出流面采用压力出口边界条件。两侧面和顶面采用对称边界条件，等价于自由滑移的壁面。计算域底面和研究对象表面采用无滑移壁面。

压力速度耦合采用SIMPLE算法，控制方程的计算残差设置为3×10－5。采用Realizable k－ε湍流模型的定常绕流计算中，动量方程和湍动能及湍动能耗散率方程均采用二阶精度离散格式;LES非定常绕流计算中，动量方程采用Bounded Central Differencing离散格式，时间离散为二阶全隐格式，以模型高度H和模型高度处平均风速UH无量纲化的时间步长Δt=0.009。

2.3 入流边界条件的生成

本文采用文献［10］改进的谱生成法合成LES入流边界条件，该方法主要思想为:先由随机方法生成一个瞬时的脉动速度场;然后，基于定常的RANS计算或试验数据得到的流场相关张量、湍流的长度和时间尺度，对前面的速度场进行修正，得到最终的速度场。文献［10］也证明了该方法得到的速度场是无散度的，具有非均匀性、非各向同性的特点，同时也具有指定的相关性。

3 结果和讨论

采用前述方法，对本文研究对象进行了数值模拟计算。(1)首先与相应风洞试验结果进行了比较，以验证采用方法的有效性;(2)然后对不同来流湍流度情况下的LES计算结果进行了比较，以研究来流湍流度对结构风压分布的影响。为便于对比，计算对象表面压力场用一个无量纲的风压系数CPi表示，定义为CPi=Pi/(0.5ρU2H)，其中 Pi是任意测点的压力(Pa)，ρ是空气密度(kg/m3)，UH为模型高度H处来流速度(m/s)。CP，mean和 CP，rms分别表示测点的平均和根方差风压系数。

3.1 数值模拟与风洞试验结果比较

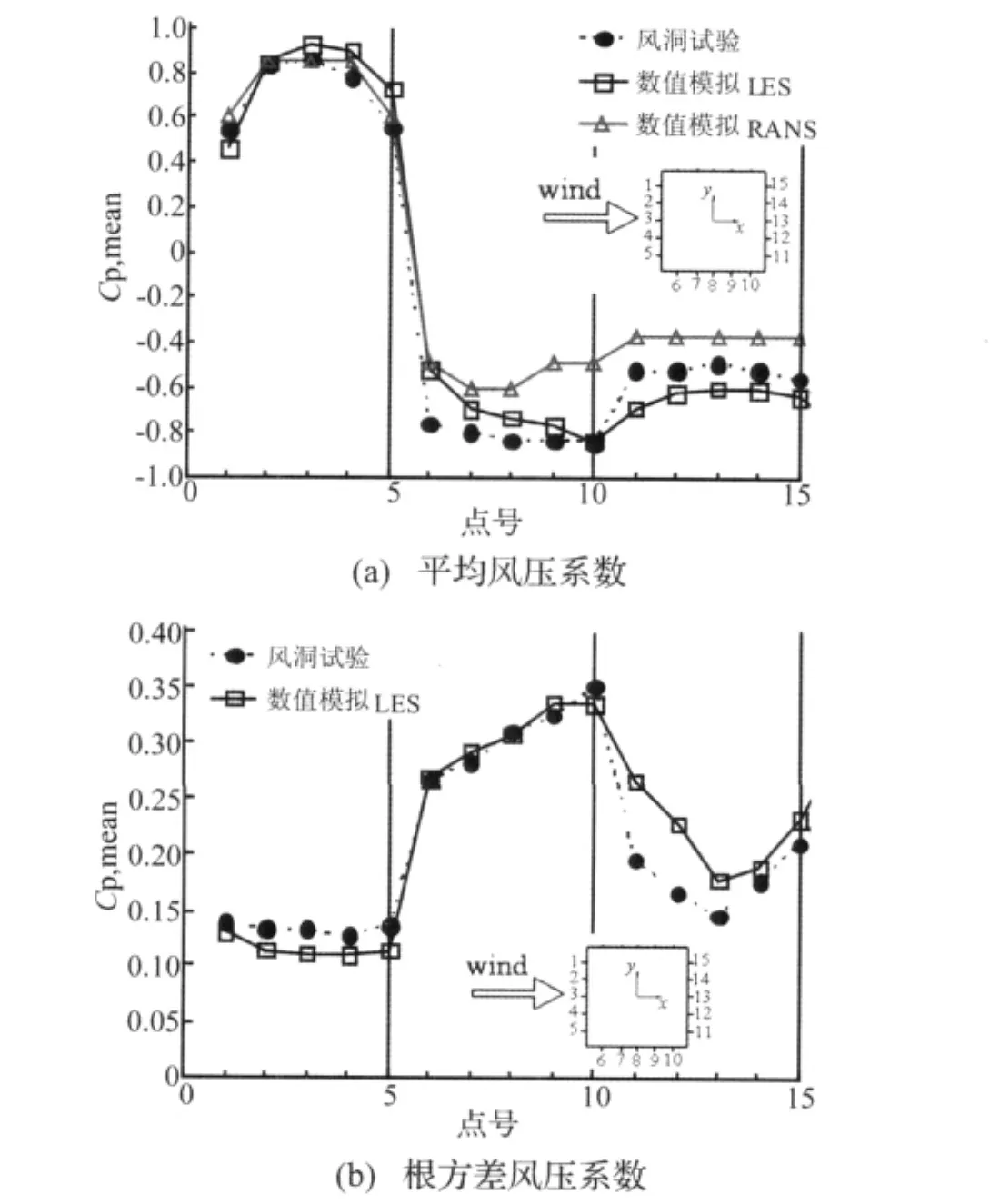
图3 测点风压系数比较Fig.3 Comparison of wind pressure coefficients of measuring points

图3为测点的平均和根方差风压系数比较，在平均风压系数的比较中，数值模拟计算包括LES非定常计算结果的统计值(以下简称LES结果)和基于RANS的Realizable k-ε湍流模型定常计算结果(以下简称RANS结果)。由图3可以看出:(1)LES结果和RANS结果平均风压系数随测点位置变化的趋势与试验值基本一致;数值上来看，在结构迎风面二者与试验值吻合较好，而在侧面和背风面则相对有误差，RANS结果误差相对较大。(2)LES数值模拟所得根方差风压系数随测点位置变化的趋势与试验值也基本一致;数值上来看，结构的迎风面和侧面LES数值模拟所得测点根方差风压系数与试验值的吻合程度优于背风面。

图4和图5分别表示方柱表面的平均和根方差风压系数等值线LES数值模拟和风洞试验结果的比较。由图4可以看出，在方柱各表面的平均风压系数分布上，LES数值模拟和风洞试验结果均基本一致。从图5的比较中可以看出，在结构迎风面的根方差风压系数分布上，风洞试验结果稍大于LES结果;侧面风洞试验值与LES结果基本一致;背风面风洞试验值与LES结果的差别大于另外两个表面，风洞试验值要小于LES结果。

图6所示为风洞试验和LES数值模拟所得测点的风压系数自谱比较，限于篇幅，这里仅给出部分测点的比较结果。由图6可以看出:在各表面上，风洞试验和LES数值模拟所得测点的风压系数自谱基本吻合，其中迎风面和侧面上的吻合程度较背风面好，这与图3所示测点的根方差风压系数计算与试验值比较结果相一致。

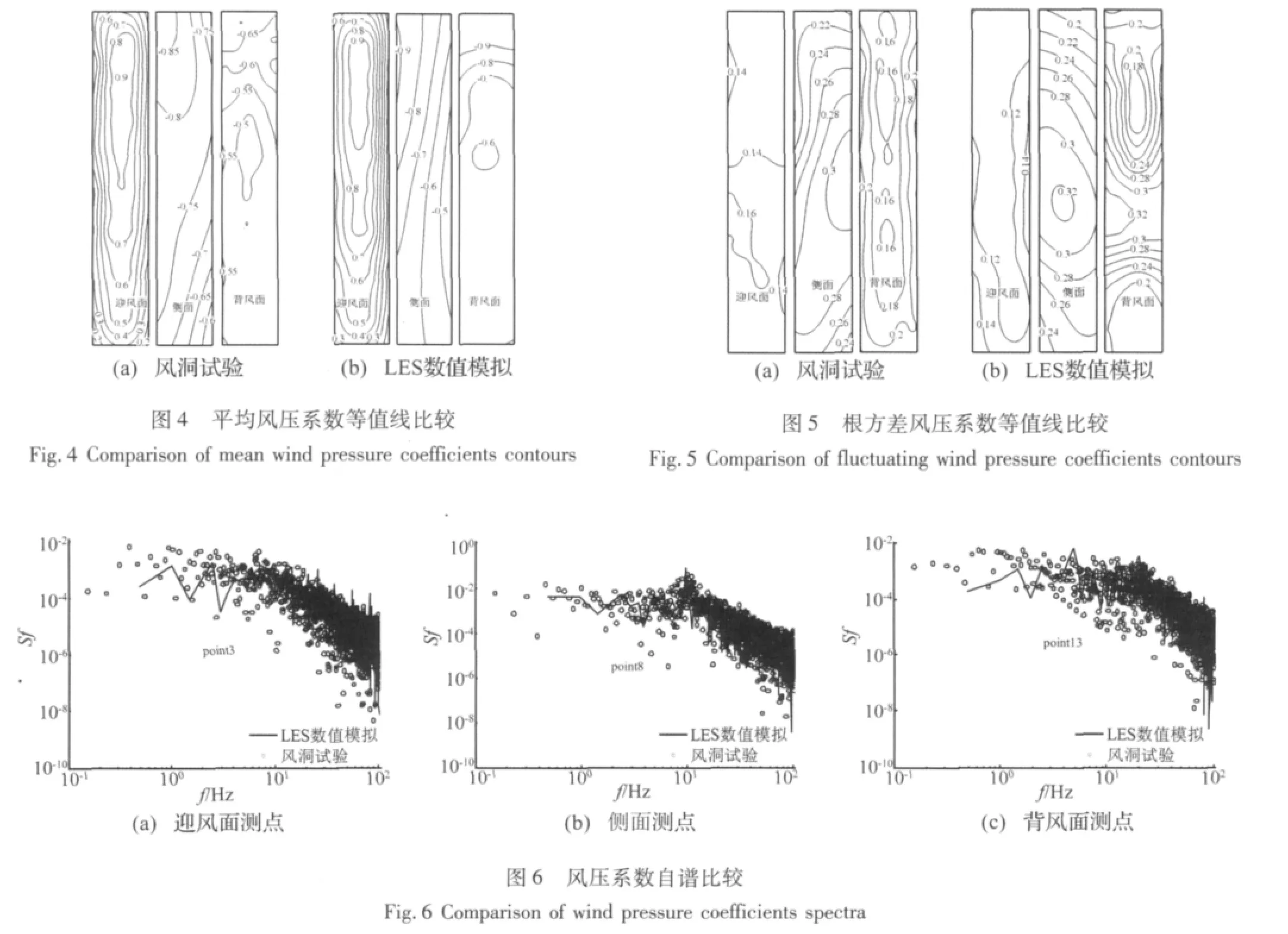
综上分析可见，在风压系数的统计特性以及自谱上，LES结果与风洞试验结果均能够基本保持一致，本文的LES数值模拟基本上能够预测结构表面的平均和脉动风压分布。

3.2 不同来流湍流度的影响

为研究来流湍流度对方柱表面风压系数，特别是根方差风压系数的影响，下面基于上述选定的LES模型和参数，对不同来流湍流度情况下结构表面的风压分布进行了研究，主要考虑了:(1)来流湍流度为0;(2)来流湍流度剖面采用风洞试验拟合曲线，即图1(c)中“拟合”和公式(3);(3)较大的来流湍流度，这里取公式(3)中IU放大1.27倍的湍流度剖面。基于上述三种工况，主要比较了测点的平均和脉动风压系数，如图7所示，图中“无”、“拟合”和“大”分别依次对应前述三种工况。

由图7可见:(1)来流湍流度的不同对结构表面的平均风压系数影响较小，而对根方差风压系数影响相对较大。(2)来流湍流度为0时，迎风面中部根方差风压系数接近0，而迎风面两侧的测点由于靠近分离区，值相对较大;随着来流湍流度的增加，迎风面根方差风压系数逐渐增大。(3)结构侧面根方差风压系数基本不受来流湍流度的影响，而背风面受来流湍流度的影响则介于侧面和迎风面之间，规律不明显。

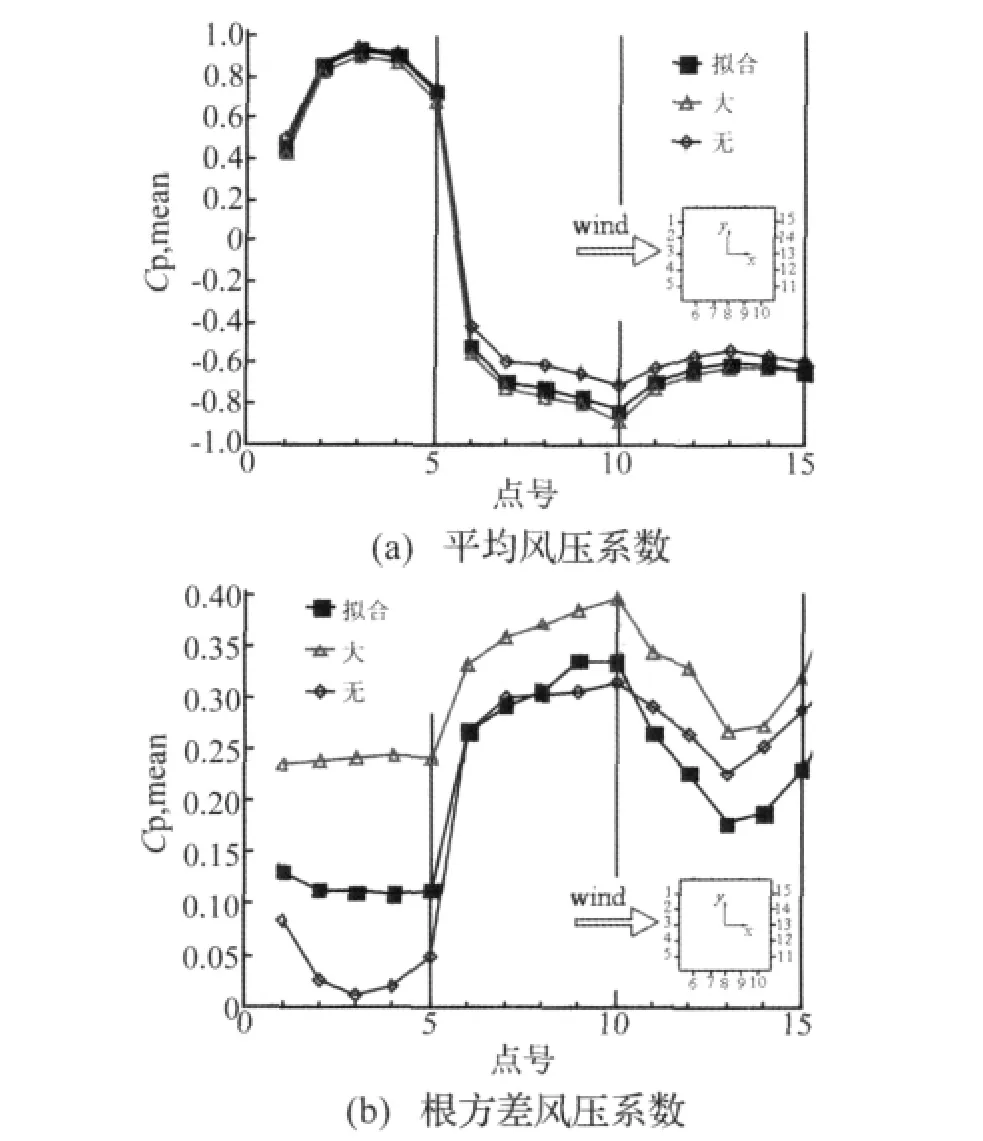
图7 不同来流湍流度时测点风压系数比较Fig.7 Comparison of wind pressure coefficients at different turbulent intensity

由此说明:对于类似本文研究的0°风向角下的方形截面建筑来说，方柱迎风面风压直接受来流湍流的影响;侧面由于存在流动分离，其风压主要受分离产生的特征湍流的影响，受来流湍流度的影响较小;而背风面则处于复杂的尾流区，其表面风压受到的影响因素则比较复杂。

4 结论

本文首先对一宽高比为1∶1∶6的单体方形截面高层建筑进行了刚性模型风洞测压试验，获得了其表面的平均和脉动风压分布。然后，基于Fluent 6软件平台，采用大涡模拟(LES)方法对该方形截面高层建筑缩尺模型表面的平均和脉动风压进行了数值模拟，并与相应风洞试验结果进行了比较和分析。最后，研究了不同来流湍流度对结构表面风压系数的影响。通过本文的研究主要得到以下结论:(1)对于类似本文研究的0度风向角下的方形截面建筑来说，结构迎风面风压直接受来流湍流的影响;侧面由于存在流动分离，其风压主要受分离产生的特征湍流的影响，受来流湍流度的影响较小;而背风面则处于复杂的尾流区，其表面风压受到的影响因素则比较复杂。(2)在风压系数的统计特性以及自谱上，LES结果与风洞试验结果均能够基本保持一致，本文的LES方法能够预测结构表面的平均和脉动风压分布。

［1］顾 明，杨 伟，傅钦华，等.上海铁路南站屋盖结构平均风荷载的数值模拟［J］.同济大学学报，2004，32(2):141－146.

［2］Meroney R N.Comparison of numerical and wind tunnel simulation of wind loads on smooth，rough and dual domes immersed in a boundary layer［J］.Wind and Structures，2002，5(2－4):347－358.

［3］陈 勇，黄本才，林颖儒，等.体育场内风流场和直缘主看台挑篷风压力分布的三维数值模拟［J］.建筑结构，2002，9:56－58.

［4］郑德乾，顾 明，周晅毅，等.世博轴膜面平均风压的数值模拟研究［J］.建筑结构学报，2009，30(5):212－219.

［5］Tamura T.Towards practical use of LES in wind engineering［J］. Journal of Wind Engineering and Industrial Aerodynamics，2008，96(10－11):1451－1471.

［6］Huang S H，Li Q S，Xu S L.Numerical evaluation of wind effects on a tallbuilding by CFD ［J］. Journalof Constructional Steel Research，2006，63(5):612－627.

［7］Nozawa K，Tamura T.Feasibility study of LES on predicting wind loads on a high-rise building［C］.In:Proceedings of 11thInternational Conference on Wind Engineering，2003，2519－2526.

［8］ Tominaga Y，Mochida A，Murakami S，et al.，Comparison of various revised k-epsilon models and LES applied to flow around a high-rise building model with 1:1:2 shape placed within the surface boundary layer［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96(4):389－411.

［9］Lim H C，Thomas T G，Castro I P.Flow around a cube in a turbulent boundary layer:LES and experiment［J］.Journal of Wind Engineering and Industrial Aerodynamics，2009，97(2):96－109.

［10］ Smirnov A， Shi S， Celik I， Random Flow Generation Technique for Large Eddy Simulations and Particle-Dynamics Modeling［J］，Journal of Fluids Engineering-Transaction of the ASME，2001，123(2):359－371.

Large eddy simulation of flow around a single square building model with 1∶1∶6 shape

ZHENG De-qian，GU Ming，ZHANG Ai-she，ZHANG Jian-guo

(State Key Laboratory for Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China)

Based on Fluent 6，the mean and fluctuating wind pressure coefficients of a high-rise building scaled model with aspect ratio of 1:1:6 were numerically simulated by adopting large eddy simulation(LES).The simulated results were firstly compared with those of wind tunnel tests.Then，the effect of incoming flow turbulent intensity on the wind pressure distribution on the structure was investigated.The results showed that(1)For similar structures，the wind pressure on the windward face is directly affected by oncoming flow turbulence，while the lateral faces are almost not affected but mainly affected by the signature turbulence caused by the flow separation;for the reason that the leeward face is located in the wake of the flow，the factors influencing wind pressure on the leeward face are relatively complex;(2)the statistic characteristics and the spectra of the wind pressure coefficients for LES results are elementarily in accordance with those of wind tunnel test results;LES technique can precisely predict the mean and fluctuating wind pressure distributions on surface of structures.

high-rise building;large eddy simulation(LES);wind tunnel test;mean wind pressure coefficient;fluctuating wind pressure coefficient

TU973+.213

A

国家自然科学基金重大研究计划重点项目(90715040);国家科技支撑计划课题(2006BAJ03B04);上海市科技攻关计划资助(09dz1207704);国家自然科学基金项目(51078225)

2009－12－07 修改稿收到日期:2010－03－09

郑德乾 男，博士生，1981年12月生