温度影响下基于主成分分析和模态柔度的结构异常检测

李 苗， 黄天立，任伟新

(中南大学 土木建筑学院，长沙 410075;2.高速铁路建造技术国家工程实验室，长沙 410075)

温度影响下基于主成分分析和模态柔度的结构异常检测

李 苗1，2， 黄天立1，2，任伟新1，2

(中南大学 土木建筑学院，长沙 410075;2.高速铁路建造技术国家工程实验室，长沙 410075)

在基于振动的结构损伤识别中，很多结构动力学的参数可用作损伤特征参数，如共振频率、振型、模态柔度等。结构损伤会引起损伤特征参数发生改变，但环境因素和运营条件的影响也会使这些特征参数发生变化，而且这种变化往往会掩盖结构自身损伤所引起的特征参数变化。如何剔除或减少诸多环境因素的影响，得到结构本身的真实状况(有损或无损)，成为了桥梁损伤检测和健康监测中的一个关键问题。选用对结构损伤较为敏感的模态柔度作为损伤特征参数，通过数值模拟算例对比分析了结构局部损伤和温度变化对模态柔度的影响;对结构在不同状态下的模态柔度进行主成分分析，用残差建立其统计分布模式，用统计模式识别的方法识别模式差异，实现考虑环境因素影响的结构异常检测。结果表明，若不考虑温度对模态柔度的影响，易对桥梁结构的健康状况产生误判;运用基于主成分分析的结构异常检测方法可有效剔除温度对模态柔度的影响，实现结构异常的检测。

主成分分析;异常检测;温度影响;模态柔度

桥梁结构健康监测过程需要在一个较长的时间段内通过一些传感器对系统的响应进行采集，从这些响应信号中提取出对结构损伤比较敏感的特征，并对这些特征进行统计分析，区别损伤与非损伤结构，达到损伤识别和结构健康监测的目的［1－3］。基于结构动力的损伤检测方法，可用结构动力学的参数作为损伤特征参数，如自振频率、频率响应函数、振型、振型的曲率、模态柔度等。在实际应用过程中，结构受到环境因素和运营条件(如温度、温度梯度、湿度、风和交通情况等)的影响，结构动力学参数会随环境因素和运营条件的改变而发生变化［4］。环境因素和运营条件的改变造成的结构损伤特征参数的变化有时会淹没或掩盖结构因损伤造成的损伤特征参数的变化［5］，如何减少或剔除诸多环境因素的影响，得到桥梁结构的真实状况，成为了桥梁损伤检测和健康监测中的一个关键问题。

考虑环境因素对结构损伤特征参数的影响主要有两种方法。通过实测，建立环境因素(如温度)与损伤特征参数(如自振频率)的相互关系是其中一种，如Z24 bridge的 AR 模型［6］，汀九桥的 SVM 模型［7］，Canyon桥的线性过滤模型［8］等。这种相关关系一般是孤立各个环境因素，如温度，拟合试验数据得到的线性关系，而结构真实的运营条件复杂，是多因素综在一起的，显然该方法有较大的局限性［9］。另一种方法是直接考虑环境因素影响的方法，即环境因素作为影响变量嵌入在损伤特征参数之中，不需区分和测量各个环境因素的影响［9，10］，利用主成分分析来剔除环境因素对损伤特征参数的影响。因此这种直接的方法具有更多优越性。

相比自振频率和振型，模态柔度对结构损伤更为敏感［11－13］。本文选用模态柔度作为损伤特征参数，首先通过数值模拟算例对比分析温度变化和结构局部损伤对模态柔度的影响;然后对结构在不同温度下的模态柔度进行主成分分析，剔除温度对模态柔度的影响，并进行结构异常检测。

1 主成分分析和结构异常检测

主成分分析是一种将原来多个变量重新组合成一组新的互相无关的几个综合变量的多元统计分析方法，其本质上是线性的分析工具。该方法可通过几个较少的综合变量尽可能多地反映出原来变量的信息。采用对损伤特征参数进行主成分分析，求主成分分析结果的残差的方法，可达到减少或剔除环境因素影响的目的。损伤特征参数经剔除环境影响后，建立结构在健康状态下经过主成分分析的损伤特征参数的统计置信区间(基准)，然后根据未知状态下同样经过主成分分析的损伤特征参数落在该置信区间的概率大小，来判断结构是否出现异常，这就是异常检测的基本思路。

Yan［14］选用自振频率作为损伤特征参数，分析并剔除了温度对自振频率的影响。本文通过求各阶模态柔度矩阵的2－范数来衡量各阶模态柔度的大小，分析各阶模态柔度在不同温度下的变化情况。

规定 ynk为 τk(k=1，2，…..，N，N 为样本数) 时刻的第n阶模态柔度矩阵的范数，构建样本矩阵Y∈Rn×N。对样本矩阵Y的协方差矩阵做奇异值分解:

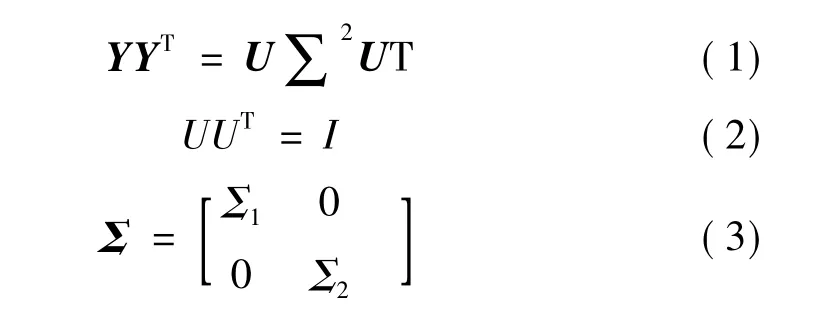
式中U为正交矩阵，矩阵中第i个列向量定义Y的第i个主成分。Σ为奇异值矩阵，根据奇异值的大小，可将矩阵Σ分为两部分:

σ1值越大，说明第i个主成分反映原变量yk的信息越多。主成分分析的目的之一是为了简化数据结构，通过较少的综合变量反映出原变量较多的信息，故在实际应用中一般不用n个主成分，而选用m(m＜n)个主成分。m的取值通过I来确定:

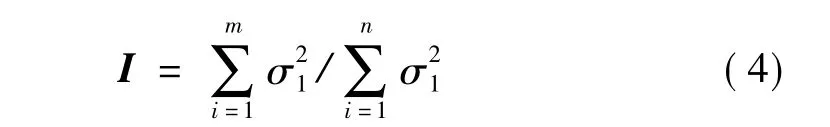
式中，I应大于一定门槛值 e(%)(即95%)［15］。门槛值说明前m个主成分能反映原变量 yk信息量的e(%)，也就是贡献率达到e(%)。本文算例中影响模态柔度的环境因素主要是温度，因此m可取1。在后面的算例分析中可以看到，m取1是恰当的。

为了剔除温度对原向量yk的影响，需要通过转换矩阵T将样本矩阵Y投影至包含温度信息的空间，转换矩阵T由U中前m列向量构成。

将重构得到的矩阵X再投影至原向量空间，计算得到样本向量yk的残差E。残差E包括了除温度以外其他影响因素(噪声等)的信息。因此，残差E的计算过程即对原向量yk剔除温度影响的过程。

计算残差E的马氏范数得到异常指数NIk，并通过异常指数建立均值控制图。

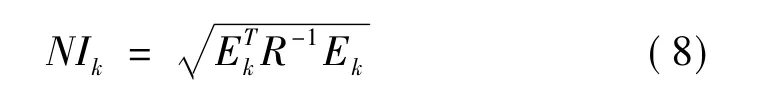
式中R=(YYT)/N是矩阵Y的样本协方差矩阵。图中上限值UCL的设置与99.7% 的置信区间对应。

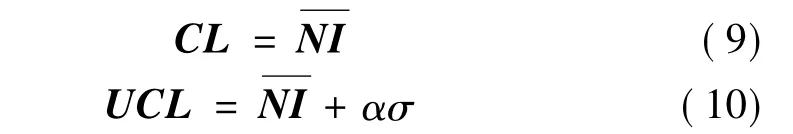
若未知状态下结构有较多的异常指数NIk(至少大于 0.3%)超过了上限值［14－16］，就认为结构可能出现了异常。

2 数值模拟算例

通过数值模拟算例，分析简支梁在不同温度和温度梯度下前三阶模态柔度的变化情况;对简支梁引入损伤(8号单元进行刚度折减)，对比分析结构损伤和温度变化对模态柔度的影响;最后通过主成分分析来考虑温度对模态柔度的影响，采用异常检测法来判断结构的健康状况。图1所示为简支梁有限元模型，共计15个梁单元。简支梁仅采用钢材，其弹性模量随温度变化的情况见图2，温度变化范围－15℃ ～45℃。考虑到桥梁健康监测系统采集的信号不可避免地受到测试误差、噪音等的影响，在数值模拟过程中对模态柔度施加1%的噪声。数值模拟算例以简支梁右端作为温度影响对比分析参考点对结构施加温度影响，简支梁两端的温度同步增加，梁中间各段的温度采用线性插值计算得到。各算例情况见表1。

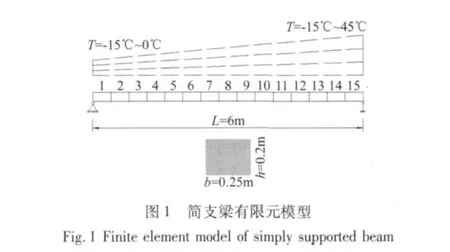
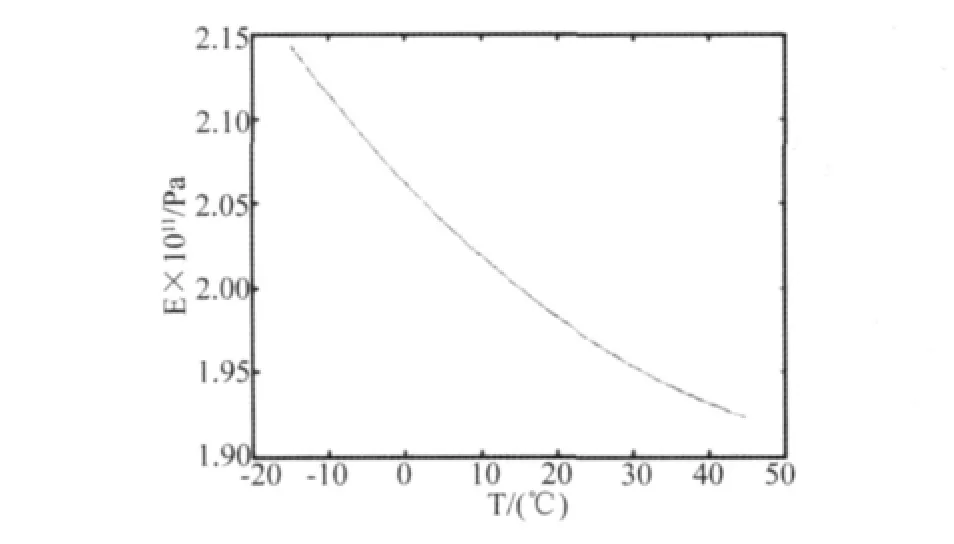
图2 钢材弹性模量随温度变化的情况Fig.2 Young modulus of steel versus temperature

2.1 温度变化对模态柔度的影响

由算例A得到简支梁在健康状态下－15℃ ～45℃的温度变化范围内前三阶模态柔度的变化情况。从图3来看，温度与模态柔度的大小存在线性关系，模态柔度的范数随温度升高而增大。对算例B、C、D进行对比分析:以算例B为基准，温度的升高(算例C)和结构的局部损伤(算例D)使模态柔度的大小出现不同程度的变化，见图4、表2～表4。

表1 数值模拟算例Tab.1 Introduction of examples

表2 算例B模态柔度的范数的变化情况Tab.2 Norm of modal flexibility of example B

图3 温度变化对前三阶模态柔度的影响Fig.3 Temperature effect on the modal flexibility of the first 3 modes

表3 算例C模态柔度的范数的变化情况Tab.3 Norm of modal flexibility of example C

表4 算例D模态柔度的范数的变化情况Tab.4 Norm of modal flexibility of example D

图4 温度变化和结构损伤对模态柔度影响的对比分析Fig.4 Analysis of effect of damage and temperature on modal flexibility

算例C前三阶模态柔度的范数均值相对算例B增幅分别为3.17%，3.73%和3.57%;算例 D 前三阶模态柔度的范数均值相对算例B增幅分别为0.79%，0%和1.56%。说明温度升高导致模态柔度的范数增大的幅度可能大于因局部损伤导致模态柔度的范数增大的幅度，图4(b)。这验证了环境因素的改变造成结构损伤特征参数的变化可能会淹没或掩盖结构因损伤造成的损伤特征参数的变化。

2.2 温度影响的剔除

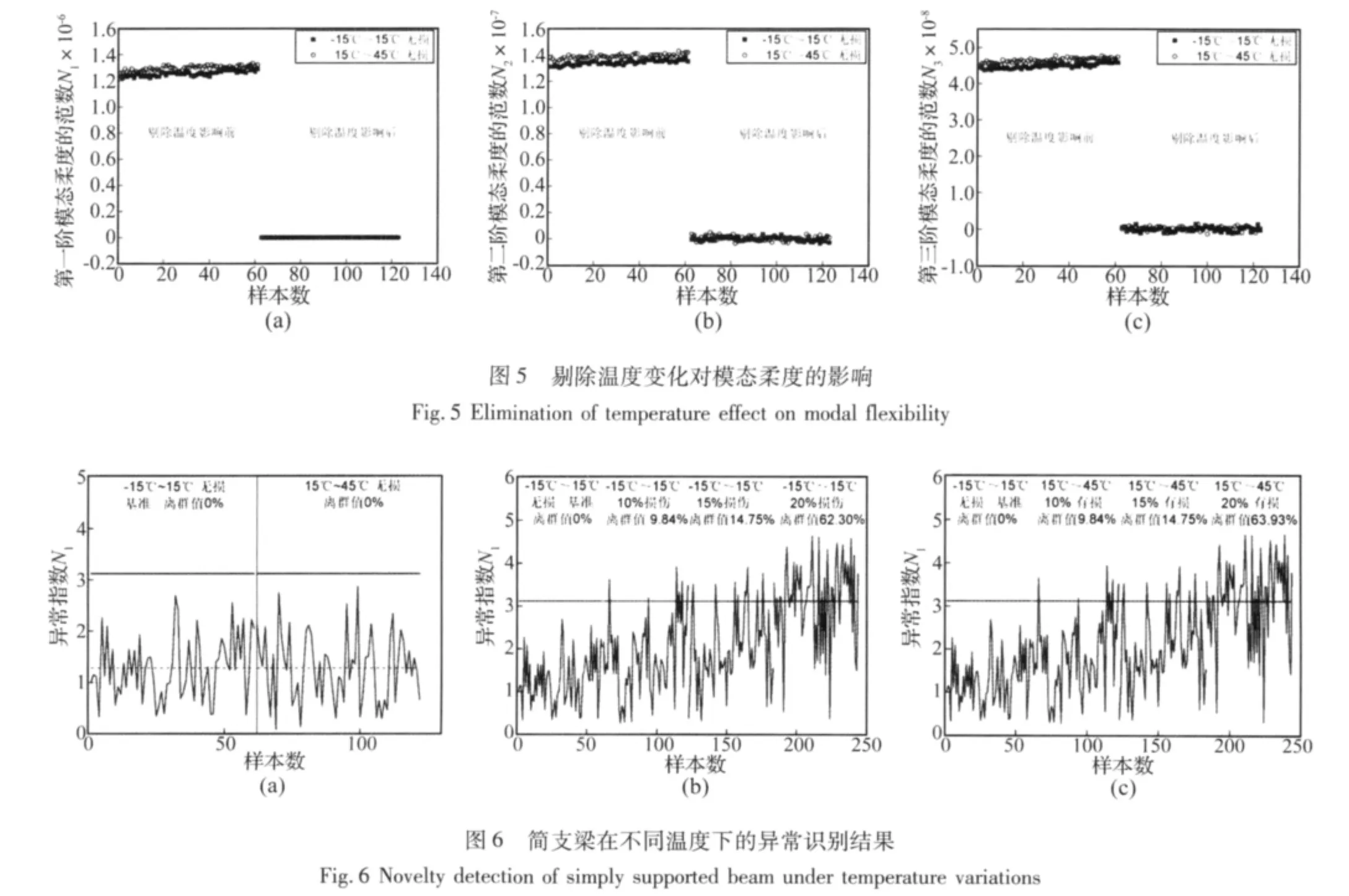
将算例B、C、D的样本代入公式(1)与(3)，得到贡献值分别为 99.832%，99.814%，99.834%，均大于99%，说明温度是影响模态柔度变化的主要因素(m=1)。对算例B和C的样本进行主成分分析，得到范数的残差未随温度的升高而增大，说明温度影响已有效剔除，见图5。

2.3 结构异常识别

由算例B(－15℃ ～15℃)的样本建立异常指数的统计置信区间，作为结构异常检测的基准。将算例B的异常指数NI代入公式(10)，得到基准的上限值(UCL)。结构在健康状态下15℃ ～45℃内(算例C)的异常指数都小于基准的上限值，说明在温度变化的情况下，未对结构的健康状况做出误判，见图6(a)。算例D～I都出现了较多的离群值(＞0.3%)，且随着结构损伤程度的加重，离群值增多，见图6(b)，(c)。结果表明，在不同温度范围内，简支梁不同程度的损伤得到有效识别。

3 结论

本文采用主成分分析的方法，用模态柔度作为损伤特征，通过数值模拟算例对比分析了温度变化和结构局部损伤对模态柔度的影响。结果表明，忽略温度对模态柔度的影响，仅根据模态柔度的变化大小来判断结构的健康状况，易导致误判。采用基于主成分分析的异常检测方法可剔除温度变化对模态柔度的影响，判断结构是否异常。多个算例验证了该方法的有效性:不同温度情况下健康结构的异常指数均未超过基准的上限值，说明主成分分析有效地剔除了温度对损伤特征的影响，不同温度范围内不同程度的损伤均使较多的异常指数超过了基准的上限值，说明正确识别结构的异常。

模态柔度虽然相对自振频率和振型而言对结构的损伤更为敏感，但仍属结构的全局参数，总体说来对结构的局部损伤依然不敏感。如果不采用模态柔度而采用其它损伤指标，本文提出的基于主成分分析和统计模式识别技术考虑环境因素影响的分析计算过程一样。

［1］宗周红，任伟新，阮 毅.土木工程结构损伤诊断研究进展［J］.土木工程学报，2003，36(5):105－110.

［2］Doebling S W，Farrar C R，Prime M B，et al.Damage identification and health monitoring of structural and mechanical systems from changes in their vibration characteristics:a literature review［R］.Los Alamos National Laboratory Report，LA－13070－MS，1996.

［3］Sohn H，Farrar C R，Hemez F M，et al.A review of structural health monitoring literature:1996－2001［R］.Los Alamos National Laboratory Report，LA-13976 －MS，2002.

［4］Sohn H.Effects of environmental and operational variability on structural health monitoring ［J］.Phil.Trans.R.Soc.A 2007，365(1851):539－560.

［5］Liu Ch Y，Dewolf J T.Effect of Temperature on Modal variability of a Curved Concrete Bridge under Ambient Loads［J］.J.Struct.Engrg，2007，133(12):1742 －1751.

［6］Peeters B，De Roeck G.One year monitoring of the z24-bridge:environmental influences versus damage events［C］.Proceedings of IMAC-XVIII，San Antonio，Texas，USA，2000:1570－1576.

［7］Ni Y Q，Hua X G，Fan K Q，et al.Correlation modal properties with temperature using long-term mentoring data and support vector machine techniques［J］.Engineering Structure，2005，27(12):1762 －1773.

［8］Sohn H，Dzwonczyk M，Straser E G，et al.An Experimental study of temperature effect on modal parameters of the Almosa Canyon bridge［J］.Earthquake Engineering and Structural Dynamics，1999，28(8):879 －897.

［9］Kullaa J.Elimination of Environmental influences from Damage-Sensitive Features in a Structural Health Monitoring Systems［A］，In:Fu-Kuo Chang(Ed.)，Structural Health Monitoring-the demands and Challenges［C］，Boca Raton，FL:CRC Press，2001，742－749.

［10］Sohn H，Worden K，Farrar C R.Novelty Detection under Changing Environmental Conditions［C］，SPIE's Eighth Annual International Symposium on Smart Structures and Materials，Newport Beach，CA.，2001.

［11］ Aktan A E，Lee K L，Chuntavan C，et al，Modal testing for structural identification and condition assessment of constructed facilities［C］，Proceedings of 12th International Modal Analysis Conference，Hawaii，USA，1994:462 －468.

［12］Pandey A K，Biswas M.Damage detection in structures using changes in flexibility［J］.Journal of Sound and Vibration，1994，169(1):3－17.

［13］颜王吉，任伟新.基于代数算法的模态柔度灵敏度分析［J］.铁道科学与工程学报，2009，6(5):37－41.

［14］ Yan A M，Kershen G，De Boe P，et al.Structural damage diagnosis under varying environmental conditions-Part I:A linear analysis［J］，Mechanical Systems and Signal Processing，2005，19(4):847－864.

［15］ Deraemaeker A，Reynders E，De Roeck G，et al.Vibrationbased structural health monitoring using output-only measurement under changing environment［J］.Mechanical Systems and Signal Processing，2008.22(1):34－56.

［16］Giraldo D F，Dyke S J，Caicedo J M.Damage detection accommodating varying environmental conditions［J］，Structure Health Monitoring，2006，5(2):155－172.

Structural novelty detection under temperature variation based on PCA and modal flexibility

LI Miao1，2，HUANG Tian-li1，2，REN Wei-xin1，2

(1.Department of Civil Engineering，Central South University，Changsha 410075，China;2.National Engineering Laboratory for High Speed Railway Construction，Central South University，Changsha 410075，China)

Damages of a structure are detected through observing changes in vibration features，such as natural frequencies，modal shapes and modal flexibility.Modal parameters are affected by not only damage in structure but also environmental and operational conditions.Compared to changes in modal parameters induced by environmental and operational effect，those by local damage in structure may be much smaller.The subtle changes caused by delicate damage in structure may be masked due to such effect.To get real state of structure，it is highly necessary to eliminate effect of environmental and operational condition on modal parameters.Modal flexibility was chosen as damage parameter for its sensitivity to damage.Via numerical model of a simply supported beam，effect of local structural damage and temperature on modal flexibility was analyzed comparatively.After principal component analysis(PCA)was applied to modal flexibility under different conditions，statistical distribution patterns were established based on the residual errors of the PCA model.The structural novelty under environmental variations could be diagnosed by recognizing difference between the patterns using the method of statistical pattern recognition.It was demonstrated that false damage diagnosis may occur without considering effect of environmental variations;PCA-based novelty detection can effectively eliminate temperature influences on modal flexibility and provide indication of structural novelty.

principal component analysis(PCA);novelty detection;temperature effect;modal flexibility

TP181

A

国家自然科学基金资助项目(50678173，50878210，51078357);863项目(2009AA11Z101);中国博士后基金项目(2008043152)

2010－03－13 修改稿收到日期:2010－10－15

李 苗 男，博士生，1980年生

黄天立 男，博士后，讲师，1977年生