复杂耦合动力系统振动响应的统计估计方法研究
廖庆斌,李舜酩,王晓东,马士虎
(1.武汉第二船舶研究所,武汉 430064;2.南京航空航天大学 能源与动力学院,南京 210016)
复杂耦合动力系统振动响应的统计估计方法研究
廖庆斌1,李舜酩2,王晓东1,马士虎1
(1.武汉第二船舶研究所,武汉 430064;2.南京航空航天大学 能源与动力学院,南京 210016)
复杂耦合动力系统是一种常见的工程力学系统,分析了复杂耦合动力系统振动响应的统计估计问题。首先通过动态系统的统计能量分析(SEA)方程,应用扰动法推导随机系统的能量平衡方程,进而推导复杂耦合系统响应的统计估计公式。在分析复杂耦合系统的响应统计估计时,重点分析各种形式激励对系统响应统计估计的影响以及载荷参数的确定方法。分析表明,相互独立的载荷作用是相关载荷作用时的一种特殊情况,它们可以应用统一的计算公式来表达。根据建立的响应统计估计方法,设计了相应的试验件,验证其正确性,试验结果表明,应用该推导得到的理论公式,系统响应的相对偏差能有效的减小,得到的能量平均值能够与试验值较好地吻合。
耦合动力系统;统计分析;载荷参数;功率流;统计能量分析
动力结构的响应特性与结构的构成、激励形式及其激励频率有关,在激励频率较低时,动力结构只有很少的几阶模态被激起,这样应用有限元方法或者边界元方法就可以精确的得到系统的动态响应,但是,当动力结构的激励频率较高(中频或者高频)、结构复杂时,动力结构的模态被大量的激起,这样要准确的计算其响应特性就变得非常困难。统计能量分析(Statistical Energy Analysis:SEA)方法正是为了适应这种需要而建立起来的一种动力结构响应分析方法,它能满足当时航天器的高频振动预示的需要,并且为分析复杂耦合系统的振动响应提供了可能[1]。和功率流方法一样,SEA也是应用能量的观点来表征结构的振动情况。
由于SEA中存在的大量的假设与逼近,使得SEA的有效性和精确性通常是未知的[2]。SEA中的响应统计估计能够使得分析对象的参数变化具有可参照性,是衡量SEA分析数据可信度的重要手段;同时,根据其响应统计估计,为后期的结构整体或局部上的改进亦能提供理论上的参考依据[3]。
Lyon[4]首先开始了对SEA分析结果统计估计的研究,给出了单点激励时结构振动响应的统计特性。后来,Davy[5]、Weaver[6]、Langley 和 Cotoni[7]等人在基于SEA的响应统计估计中做了大量的工作,促进了这一研究的发展[3]。
文献[8]分析了相关激励作用下,简单结构的振动响应的统计估计方法,本文在该文的基础上,进一步分析复杂耦合动力系统的响应统计估计。首先通过动态系统SEA能量平衡方程,应用扰动法推导随机系统的能量平衡方程,进而得到复杂耦合系统响应的统计估计公式。在分析复杂耦合系统的响应统计估计时,重点分析各种形式激励对系统响应统计估计的影响以及载荷参数的确定方法。根据建立起来的复杂耦合动力系统的响应统计估计方法,设计相应的试验件对其进行试验验证。试验结果表明,应用本文得到的理论结果,能与试验值较好的吻合,相对偏差较小。本文建立起来的响应统计估计方法,计及了各种激励条件对系统响应统计估计的影响,能够有效的反映出系统中参数对各个子系统响应的影响。
1 系统的能量平衡等式
在应用SEA分析系统的动态特性时,需要首先将系统划分为若干个子系统。设第j个子系统在振动频率为ω时的能量表示为Ej,按照Lyon和DeJong的假设[9],有:

式中:ηj是子系统 j的损耗因子,nj是模态密度,Pin,j是输入到子系统的外部功率,ηjk是子系统j到子系统k的耦合损耗因子。子系统的能量Ej通过总体随机系统的能量平均得到,如Pin,j表示的是总体平均能量的输入,ω表示频带的中心频率。
系统在共振区时,可以假设系统总能量Ej是系统的动能Tj的两倍,即

对于带宽系统,动能Tj与频带平均动能关系表示为:
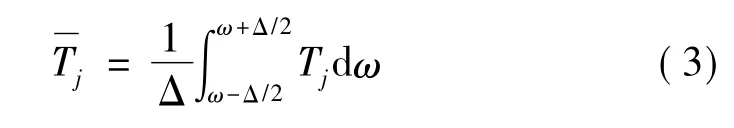
Δ为频率平均带宽。同样,对于输入能Pin,j有:

式(4)中,Pj为子系统j的功率输入为频带平均功率输入。这样,式(1)可以用矩阵的形式表示为:


根据文献[7],对于确定性系统,能量平衡等式表述为:

2 随机系统的能量平衡等式
对于船舶、车辆和飞机等复杂结构的设计而言,整个结构和其子系统都可能在设计的前期、设计过程中以及设计的后期被修改,或者由于加工的原因使得同一子系统在同一批次的产品中具有不同的特性,为了分析系统的响应统计特性,首先需要将分析系统随机化。对于随机系统的分析而言,扰动法能够有效的分析系统随机化带来的影响[11]。
相对于确定性系统,假设输入功率的确定性部分为Pin,扰动部分为Pran,这样输入功率表示为:

同理,对于矩阵D的确定性部分D0和扰动部分Dran有:

这样,结合等式(7),有如下等式成立:


应用扰动理论展开式(9),忽略二次以上的扰动项后并对等式两边取数学期望,得到:
这样,由等式(5)、等式(11)和等式(12),得到:

这就是说,随机系统的确定性部分D0可以依据确定性系统的系数矩阵来确定。
对于随机系统的能量平衡等式(7),可以得到系统的总功率Ptot为:

将等式(9)代入,将上式进一步化为:

根据系统总体能量一定的观点,对于随机系统,系数矩阵 Dran,jk的作用项,其能量为零,即等式(15)中有:


上式表明响应功率的系数矩阵,其随机部分每列的和均为零。
3 复杂耦合系统的响应统计估计
对于要分析的系统,为了评价SEA方法的有效性,需要对SEA的分析结果进行数学统计分析,这也就是本文所说的复杂耦合系统响应的统计估计。
根据前面的分析,由等式(10)、式(11)和式(12),有:

其中,r2为子系统的相对偏差,αk为载荷类型参数,αks为耦合系数,它由子系统s作用于子系统k的特征力决定。其中,m'k和B'k分别为:

由式(20)可知,为了得到子系统的能量方差,就是要确定 Var(Pran,j)和 Var(Dran,ks)的取值,而这两个参数又与载荷参数α直接关联,下面分析各种形式激励下,载荷参数α的求解。
4 参数α的取值分析

对于复杂系统,参数α的取值变得非常复杂,下面分情况讨论α的取值。
对于复杂系统,模态振型依然假设是相互独立的,这样主要就是要讨论不同的载荷形式下,对参数α取值的影响。
4.1 不相关多载荷作用的影响
本节讨论N个不相关的载荷作用在系统中不同的子系统上时,参数α的取值情况。由等式(14)知,系统输入的总功率为:
文献[8]中分析了简单随机结构中参数α取值情况,本文进一步分析对于复杂的组合系统,参数α的取值情况。依据文献[9],载荷参数α的表达式为:

又设fl为第l个载荷的广义力,在这种情况下,an表示为:

同样,为了求得参数α的值,先假设各个作用力相互独立,这样

展开式(29),只有在l=n并且m=k以及l=k并且m=n时,其值存在(其它情况下,其值为零),这样由式(29)得到:



当组合系统简化到只有一个子系统(此时子系统就是前面所指的整个系统)时,上式变成了一个恒等式。
对于随机变化的多个相互独立的分布力作用于各个子系统,记Sfi为作用力fi的自谱;Sfifj为作用力fi和fj的互谱。那么an的表示形式为:


假设每个子系统的输入功率相同,那么同式(32)一样,可以将参数α的值表示为:

同样,当组合系统简化到只有一个子系统时,上式也变成了一个恒等式。
4.2 相关激励作用的影响
上面的讨论中,在分析各种受力情况时,均是假设作用力相互独立,而当激励力不能当作相互独立来处理时,上述表达式将极大的复杂化甚至不可解。直接处理相关激励的作用,根据工程经验,几乎是不可行的[12]。为了使得分析相关激励作用下参数α的值可行,应用在文献[8]中提出的相关激励的解相关方法来处理。
对于作用在系统上的相关载荷 Fj(x),将其分解为:
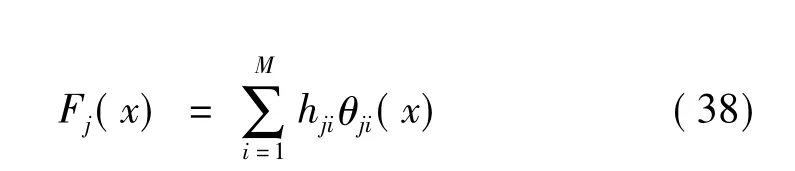
式中,θji(x)为分解得到的基函数,hji为分解系数。这样广义力可以相应的表示为:
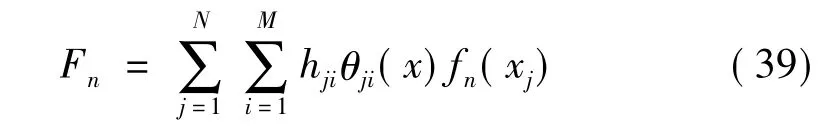
在相关激励作用下,应用式(38),可以将an表达为:

由于分解后得到的广义力是相互独立的,这样,结合等式(30)、式(39)和等式(41,可以得到:

式中,参数αcor,l为系统中第l个子系统上受相关力作用时的值。

这样,相关力作用下,复杂系统的载荷参数α为:上式与在假设载荷独立时的表达式基本是相同的,当载荷独立时,αcor,l=αl,这也就是说,对于复杂系统而言,激励独立作用也可以看成是相关激励输入时的一种特殊情况。
应用各个子系统的功率表示方法(这也是不将等式(43)应用等式(39)进一步带入展开的原因所在),参数α可以写为:

对于随机变化的多个相关力作用的各个子系统,若通过解相关后,它们的功率仍然相等,那么参数α可以表示为:

比较等式(32)与等式(44)以及等式(37)与等式(45)可知,在考虑相关激励对系统的作用时,只需应用文献[8]给出的方法求得各个子系统受相关力作用时的参数αcor,l,然后带入相应的公式就可以得到整个系统的载荷参数α,但是有一点需要注意的是:在求输入功率时,应该应用解相关后的激励力带入式(45)进行计算。
通过上面的分析可以看出,不相关激励只是本文所述相关激励的一种特殊情况,它们可以用统一的公式来表示。
5 板架系统的响应统计估计试验
5.1 试验件的构成
为验证上述理论,设计了一套由三块板连接组成的简单板架系统,它能示意性的表达出复杂系统中振动功率流的传递关系,并且也便于检验本文所给出分析理论的正确性。在试验中,各个参数(包括模态密度、耦合损耗因子、内部损耗因子等)参照文献[9]以及文献[13]中的计算公式和试验方法得到。
试验件的基本结构如图1所示,从左到右三块铝板依次编号为A,B,C,其中,板A和板C的几何参数是一样的,铝板的密度为ρ=2.7×103kg/m3,弹性模量为7.1 × 1010Pa,泊松比为 0.32,各个板的参数如表 1所示。

表1 试验中各个板的参数Tab.1 Parameters of the experimental plates
试验时,三块铝板通过螺栓连接起来,构成一个“工”字形的组合系统,两块侧板与中间的板B通过上下两个铝制的角铁固定,整个试验装置呈左右对称结构。
5.2 测试系统
三个激振器通过同一个信号发生器产生输入信号:信号发生器产生的信号通过一个多接口转换头传输到三个功率放大器,然后分别接到三个激振器上,其中两个激振器作用在板A上,一个激振器作用在板B上。为了表达输入的随机性,在板A上任意选定两个作用点作为激振器的输入点,同样,在板B上任意选定一点作为激振器的输入点。为了构造相关输入,在激振器与侧板的连接间,加一个厚1 mm、宽65 mm的“U”形铝块。在试验件的三个板上分别装上加速度传感器:板A上装有4个,板B上装有2个,板C上装有3个,整个测试示意图如图1所示。
试验中时,将试验件放在软质聚胺脂泡沫上(如图1),待各个试验器件按照图2连接完成后,开始试验。

5.3 试验数据分析
为了验证本文提出的复杂耦合动力系统振动响应的统计分析方法,用公式(1)计算系统中各个部分的振动响应。试验时,测试频率的范围为0.2 kHz~5.0 kHz,采样频率为20 kHz,共进行15次测试。在每次测试中,每块板上加速度传感器的位置随机更换3次,即每次测试更换传感器位置24次(4×2×3),进行30次采样(试验时,连续采样一段数据信号,分析时将采样数据分成互不重叠的30段处理),这样可以得到各个板平均能量随频率的变化曲线如图3所示。图中平滑曲线为应用SEA方法计算得到的能量平均值(该均值计及了相关激励作用的影响),波动曲线为试验得到的平均值曲线。

图3 三块板的平均能量随频率变化的对比Fig.3 The comparison of the average energy of three plates contrast with the frequency change
从图6可以看出,三块板响应的平均能量从大到小依次为板A,板B,板C。在频率低于1.5 kHz时,由试验得到的平均能量与由SEA理论计算得到的平均能量差别较大,这可能是由于以下几个因素导致的:
(1)在低频部分,整个系统的模态重叠率较低,使得输入能量不能在共振频带内有效的传递。
(2)输入激励是经阻抗头用螺杆连接在相应的板上,而这一结构将会在板上产生一个等效质量Me,这相当于增加了板上附加质量部分,使得测试得到的振动响应量减小,因而由试验测得的平均能量偏小。
(3)在考虑相关激励输入时,本文假定系统是保守耦合的,没有计及间接耦合的能量损耗[14],这部分能量损耗导致了试验测得的响应能量减小。
随着频率的增加,能量能够在三个板中有效的传递,附加质量的影响逐渐减小(输入功率与频率成正比而与附加质量Me成近似反比关系[15]),这使得试验得到的能量均值与理论预测吻合较好。
下面通过图的形式比较相关激励对平均能量分析的影响。当不考虑相关激励的影响时,即将图1中三个输入激励各个单独计算,此时得到板的响应的平均能量如图4所示(图中同一种线形表示一块板的变化情况,其中线上带点的表示考虑了相关激励影响得到的平均能量,波动的变化曲线为由试验得到的平均能量值)。
由图4可以看出,当不考虑相关激励的影响时,理论计算得到的平均能量比考虑相关输入情况得到的平均能量大,并且随着频率的增加,两者间的差值呈减小的趋势:当频率小于2.0 kHz时,两者之间的差值在3 dB左右,当频率在2.0 kHz与4.0 kHz间时,两者间的差值在2 dB左右,当频率大于4.0 kHz时,两者之间的差值进一步减小至1 dB左右。从试验曲线可以看出,计及相关输入时得到的理论值与试验值吻合较好,这就是说,计及相关输入,能有效的减小SEA分析得到的能量均值,更加符合工程实际情况。

图4 平均能量变化趋势的对比Fig.4 Comparison of the trends in average energy
下面分析系统受相关激励作用时,其相对偏差的情况,三块板响应的相对偏差如图5至图7所示。

在图5至图7中,由虚线表示的平滑曲线表示相对偏差的均值(由它给出相对偏差的变化趋势),实线表示各个板相对偏差的变化情况。从这三个图可以看出,随着频率的增加,各个板响应的相对偏差逐渐减小。对于本文给出由三块板组成的耦合系统,当频率大于2.0 kHz时,整个系统的相对偏差小于5,也就是说,在频率大于2.0 kHz时,整个系统的估计是比较准确的。
为了比较三块板得到的响应相对偏差,将它们表达在图8中。由图8可以知道,三块板振动响应的相对偏差从大到小依次为板C,板B,板A,也就是说,从系统中能量输入到系统中子系统的响应,随着传递路径的增加(即传递路径加长),子系统响应的相对偏差逐渐增大。对于系统处于等价传递位置上的构件,模态密度越大,其响应的相对偏差逐越小。从等式(20)知,系统响应的方差由输入功率的方差及SEA平衡方程的系数矩阵决定,对于复杂耦合系统而言,系数矩阵由系统自身的特点确定,因此为了减小能量响应的方差,需要考虑输入功率的情况,而输入功率的相关性作用直接影响输入功率方差的计算,故而计及相关激励影响的作用,能有效的减小子系统响应的相对偏差,提高分析精度。

图8 三块板相对偏差随频率变化的对比Fig.8 The comparison of the relative deviation of three plates contrast with the frequency change
6 结论
本文分析了复杂耦合动力系统振动响应的统计估计问题。总结起来,得到的结论概括如下:
(1)分析了复杂耦合动力系统的响应统计估计以及载荷参数α的确定方法。当载荷作用在子系统上时,载荷参数α与子系统上的输入能量和整个系统的输入能量的比值以及子系统上的载荷参数αl有关。当载荷相关时,应用解相关后的载荷带入载荷参数计算表达式进行计算。
(2)用试验验证了复杂系统的响应统计估计。试验表明,考虑相关激励的影响,能够使得计算得到的平均能量与试验值更好的吻合。
(3)依据试验分析了相对偏差的影响。随着频率的增加,响应的相对偏差逐渐减小,并且随着传递路径的增加,子系统响应的相对偏差逐渐增大。由于输入功率的方差受相关激励的影响,因而考虑相关输入的影响,能有效的减小各个板的振动响应的相对偏差,即增加分析的准确性。
[1] Langley R S,Bardell N S.A review of current analysis capabilitiesapplicable to the high frequency vibration prediction of aerospace structures[J].The Aeronautical Journal,1998,102(1015):287 -297.
[2]Culla A,Sestieri A.Is it possible to treat confidentially SEA the wolf in sheep's clothing? [J].Mechanical Systems and Signal Processing,2006,20(6):1372 -1399.
[3]廖庆斌,李舜酩.统计能量分析的响应统计估计及其研究进展[J].力学进展,2007,37(3):337-345.
[4]Lyon R H.Statistical analysis of power injection and response in structures and rooms[J].Journal of the Acoustical Society of America,1969,45(3):545 -565.
[5]Davy J L.The relative variance of the transmission function of a reverberation room[J].Journal of Sound and Vibration,1981,77(4):455-479.
[6]Weaver R L.On the ensemble variance of reverberation room transmission functions,the effect of spectral rigidity[J].Journal of Sound and Vibration,1989,130(3):487 -491.
[7]Langley R S,Cotoni V.Response variance prediction in the statistical energy analysis of built-up systems[J].Journal of the AcousticalSociety ofAmerica,2004, 115(2):706-718.
[8]廖庆斌,李舜酩,辛江慧,等.相关激励作用下随机结构振动响应的统计分析[J].振动工程学报,2008,21(5):429-435.
[9]Lyon R H,Dejong R G.Theory and Application of Statistical Energy Analysis,2nd Ed[M]. Boston: Butterworth-Heinemann,1995.
[10] Langley R S.A general derivation of the statistical energy analysis equations for coupled dynamic systems[J].Journal of Sound and Vibration,1989,135(3):499 -508.
[11]陈塑寰.结构振动分析的矩阵摄动理论[M].重庆:重庆出版社,1991.
[12] Lin Y K.Probabilistic Theory of Structural Dynamics[M].New York:McGraw-Hill,1967.
[13] Bies D A,Hamid S.In situ determination of loss and coupling loss factors by the power injection method[J].Journal of Sound and Vibration,1980,70(2):187 -204.
[14] Sun J C,Wang C,Sun Z H.Modification of energy balance equation in statistical energy analysis[J].Chinese Journal of Acoustics,1996,15(1):1 -7.
[15] Cotoni V,Langley R S,Kidner M R. Numerical and experimental validation of variance prediction in the statistical energy analysis of built-up systems[J].Journal of Sound and Vibration,2005,288(3):701-728.
Statistical analysis for vibrational response of a complicated coupled dynamical system
LIAO Qing-bin1,LI Shun-ming2,WANG Xiao-dong1,MA Shi-hu1
(1.Wuhan Second Ship Design and Research Institute,Wuhan 430064,China;2.Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
The statistical characteristics of vibrational response of a coupled dynamical system were analyzed here.At first,the equation of energy balance of a random dynamical system was gained based on statistical energy analysis(SEA).Then,the statistical estimation expression was deduced for the vibrational response of the coupled dynamical system.the influence of all kinds of excitation on the statistical estimation and the method of determining loading parameters were analyzed.It was shown that the independent excitation is a special case of correlated-excitations,they can be expressed with an uniform expression.Test samples were designed to validate the correctness of the method based on the estimation expression.The experimental results showed that the statistical analysis method proposed is more accurate than the existing ones,it can reduce the relative deviation of vibrational response effectively.
coupled dynamical system;statistical analysis;loading parameter;power flow;statistical energy analysis
TB53;O324
A
国家自然科学基金资助项目(50675099)
2010-01-15 修改稿收到日期:2010-04-06
廖庆斌 男,博士,1979年6月生

