山地超高层建筑风致响应研究
李正良,魏奇科,黄汉杰,孙 毅
(1.重庆大学 土木工程学院,重庆 400045;2.中国空气动力研究与发展中心低速空气动力研究所,四川 绵阳 621000)
山地超高层建筑风致响应研究
李正良1,魏奇科1,黄汉杰2,孙 毅1
(1.重庆大学 土木工程学院,重庆 400045;2.中国空气动力研究与发展中心低速空气动力研究所,四川 绵阳 621000)
风在山地地形的干扰下,其幅值和空间分布规律相对平地均会发生较大改变,尤其是山顶处风速有明显增大。如果不考虑山地的影响,仍然用平地边界层风场进行高层建筑维护结构和整体结构计算将偏于不安全。以前对山地风场的研究多限于平均风的变化,而对于脉动风的湍流特征和频域特性较少提及,且缺少山地与平地风场中超高层建筑风致响应计算的对比。本文建立了钟形、高斯形、余弦型几种轴对称三维山体模型,通过数值计算得到了不同山体坡度下山顶平均风加速比。计算结果显示,山顶平均风有较大的增大效应,最大加速比可达1.7,且反函数拟合结果与模拟结果更加吻合。通过与风洞试验结果的对比可见,平均风的数值模拟有较高准确性,湍流与试验相比还有一定差别。通过某超高层建筑的风振响应分析表明,山地风的增大效应对超高层建筑整体响应计算不可忽略,位移响应增大比例最大可达20%。
山地风场;CFD;风洞试验;超高层建筑;风致响应
大气边界层在山地地形的影响下,其幅值和空间分布规律均会发生较大改变。很多学者针对山地风场进行了风洞试验、数值模拟以及现场实测研究。Taylor[1,2]总结了早期的一些研究成果,并运用混合谱有限差分法(MSFD)及非线性混合谱有限差分法(NLMS-FD)对山地风流动进行了计算,结合风洞试验结果提出了山地风计算模型;Miller,Davenport[3]进行了一系列二维复杂山体的风洞试验,并与加拿大、英国规范和MSFD模型进行了对比,得出了规范偏保守的结论;Weng[4]基于MSFD和NLMSFD的计算结果,考虑了表面粗糙度和风速增大系数的非线性,提出了新的风场模型;Kim[5,6]对四处典型山地地形进行了数值模拟,选用了标准k-ε模型和RNG k-ε模型两种湍流模型,通过与现场实测数据的对比,认为数值模拟可以作为复杂山地风场预测可靠的工具;Carpenter[7]进行了1:1 000比例的二维山地风洞试验,包括坡度较小和较大的正弦截面山体、多个连续山体以及不规则山体;T.Takahashi[8]利用热线风速仪测量了两种不同表面粗糙度下二维山体近地平均风剖面、湍流度、雷诺应力、湍动能和湍流粘性剖面,分析了不同粗糙表面山体的湍流特性;同时,一些国家和地区规范按地形条件提供了地形影响系数以供参考。
但已有研究均只针对山地平均风,对于山地风的湍流特征和频域特性研究较少,对山地风作用下超高层建筑的响应研究也较少。
1 山地平均风加速比
1.1 加速比模型
加速效应(speed-up effect)指在山地地形中,某高度平均风速比平地相应高度平均风速有所增加的效应,一般在山顶的近地面最为明显。通常用一个无量纲的参数:加速比(speed-up ratio)来定量描述加速效应:
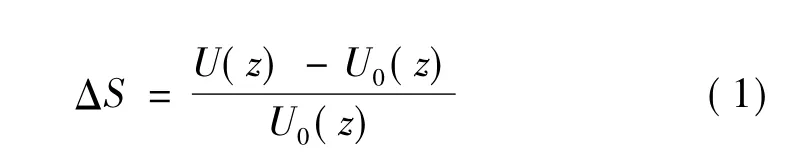
式中:U(z)表示山地地面以上z高度处的风速,U0(z)表示平地地面以上z高度处的风速。
针对山顶加速比,Jackson和Hunt[9]最先提出了一种计算二维光滑山体加速效应的解析算法,但这种算法仅仅适用于未发生流动分离的情况;随后Jackson[10]运用风洞试验和数值模拟检验了这种算法;Hunt[11]又对其提出了修改,使之更加趋于完善。Mason和Sykes[12]在Jackson等人的基础上,将其算法延伸到单个三维山体的情况。Kaimal和Finnigan[13]通过研究指出,以Jackson和Hunt的方法为主体的算法,在计算未发生流动分离时的最大加速效应误差可以小于15%到18%。
Jackson和Hunt[9]提出的算法中,对于最大加速比的规定为:
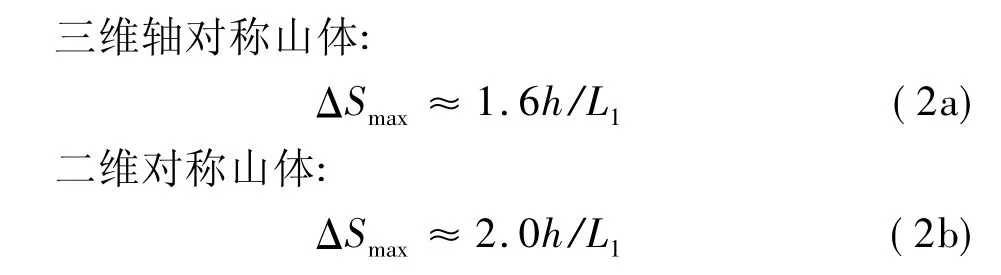
Taylor和 Lee[14]的在 Jackson算法基础上提出了“原始算法”,可以计算山顶不同高度处的加速比:
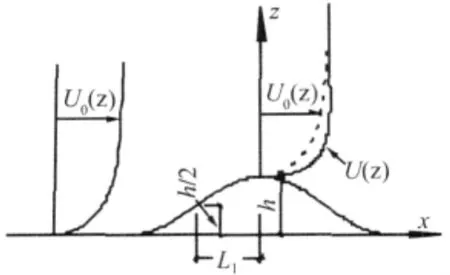
图1 山体形状及加速效应示意图Fig.1 Schematic diagram of a hill and the speed-up effect
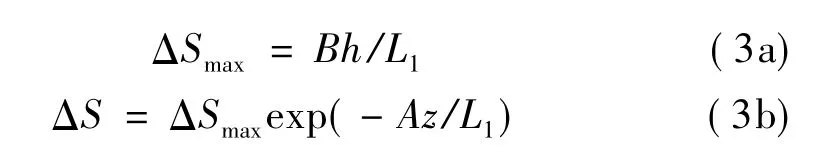
1.2 一些国家和地区风荷载规范关于地形修正系数的建议
1.2.1 中国规范[15]
风压高度变化系数考虑地形条件的影响系数在山顶处可用以下公式计算:
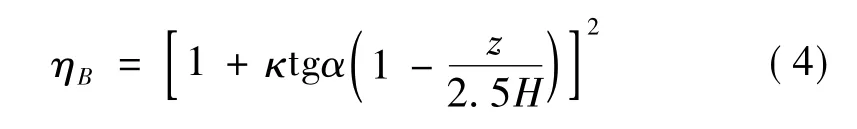
tgα是山峰或山坡在迎风面一侧的坡度;κ是系数,对山峰取3.2,对山坡取1.4;H是山峰或山坡高度;z是建筑物计算位置离地面的高度(当z>2.5H时,取z=2.5H)。对于山峰和山坡的其他部位,影响系数按η的线性插值确定。
1.2.2 美国最小荷载规范(ASCE)[16]
风速地形增大因子Kzt,其表达式如下:
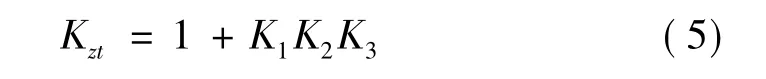


表1 美国规范中地形影响系数各参数的取值Tab.1 Coefficients for Kztin ASCE
美国规范总结了 Taylor[1,2]和 Weng[4]的研究成果,综合考虑了地貌类别,山体形状,山体坡度等的影响。
1.2.3 加拿大规范及ISO标准
加拿大规范[17]及 ISO 标准[18]的思想同美国规范基本相同,仅K1的系数取值不同:
(1)加拿大规范不考虑地貌类别差异,山脊、陡坡和小山各地形 K1的系数分别为2.2、1.3 和1.6,比美国规范各类地貌K1的系数都大;
(2)ISO标准也不考虑地貌类别差异,山脊、陡坡和小山各地形 K1的系数分别为 2.0、1.8 和1.6。
1.2.4 日本规(AIJ)[19]
地形影响系数可由式(6)确定。
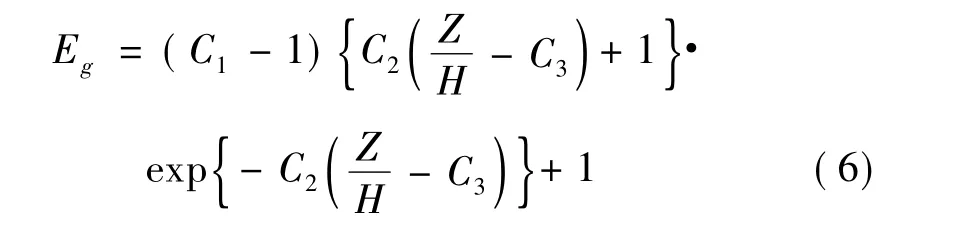
1.2.5 澳大利亚规范(AS/NZS)[20]
① 当 H/2Lu<0.05 时,Mh=1.0;
② 当0.05≤H/2Lu≤0.45 时,
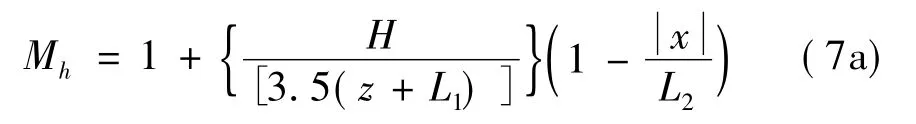
③ 当H/2Lu>0.45时,山顶近地面的流动分离区
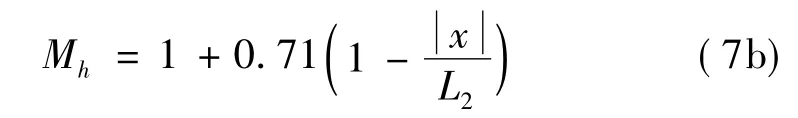
H是小山、山脊或陡坡的高度;Lu是小山、山脊或陡坡顶至半山高的水平距离;x是建筑物上风向或下风向至山顶的水平距离;L1取0.36Lu或0.4H的较大值;L2除了陡坡的下风向取10L1外,其他均取4L1;Z是离地面高度。
1.2.6 不同规范的对比分析
一个三维山体,高150 m,半山高到山顶的距离300 m,坡度h/L1=0.5。根据各规范计算的山顶平均风增大系数见图2。
可见,根据各参考模型计算的山顶位置平均风增大系数相差较大。中国规范计算值最大,美国规范次之,日本和澳大利亚规范接近。并由此说明,山地风场平均风的加速效应仍然没有一个相对一致的研究结果。

2 山地风场特性数值模拟
2.1 几何建模及网格划分
本文采用Fluent建立模型进行数值模拟。计算域在竖直方向取为10 H,模型上游10 H,下游20 H,宽度20 H,模型采用六面体映射网格划分计算区域。山体近壁网格划分较密,取网格竖向尺寸为H/150,远离壁面网格尺寸为H/2。山体的几何模型及网格划分如图3所示。
2.2 边界条件设定和求解设置
入流面选用速度进口边界。速度剖面选用中国规范B类场地,取α=0.16。湍流度剖面和湍流积分尺度参考日本规范。
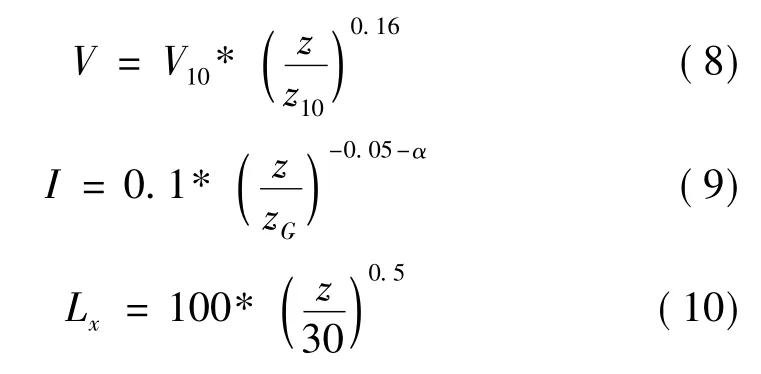
在入流处直接给定湍动能k和湍流耗散率ε:

出流面采用自由出流边界,流域顶部和两侧采用对称边界,等价于自由滑移壁面边界。地面采用无滑移的壁面条件,且在地面引入粗糙壁面修正[21]。由于钝体绕流将出现分离、再附、冲撞、环绕及旋涡等复杂的流动,所以选用非平衡壁面函数来模拟壁面附近复杂的流动现象。
压力-速度求解选用耦合算法求解,同时选用二阶迎风格式离散控制方程,以减少假扩散误差。湍流模型采用RNG k-ε模型,可较好的处理高应变率及流线弯曲程度较大的流动[22]。
2.3 山体形状影响
常用的山体形状模型包括钟型、高斯型和余弦型。
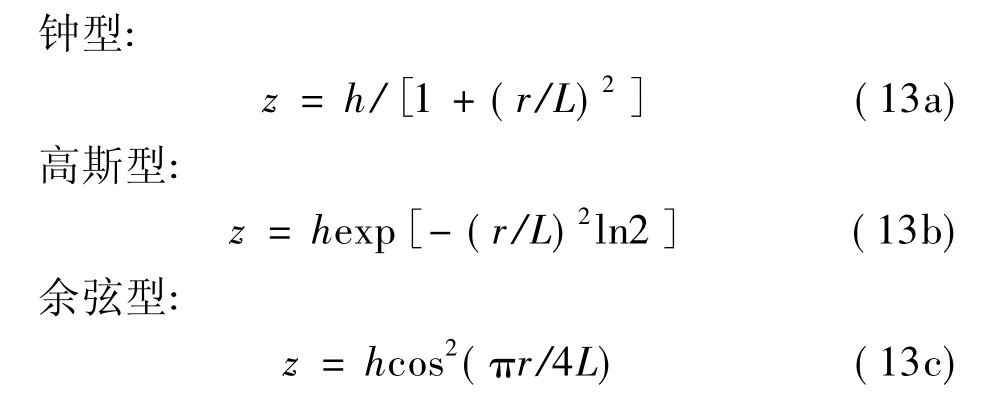
式中:r为到山顶的水平距离,h是山体高度,L是山顶到半山高度处的水平距离。图4是不同山体形状加速比计算结果。
可见,山体形状对山顶平均风加速比影响不大。因此本次模拟和相关试验就采用同一种山体形状——余弦型山体。
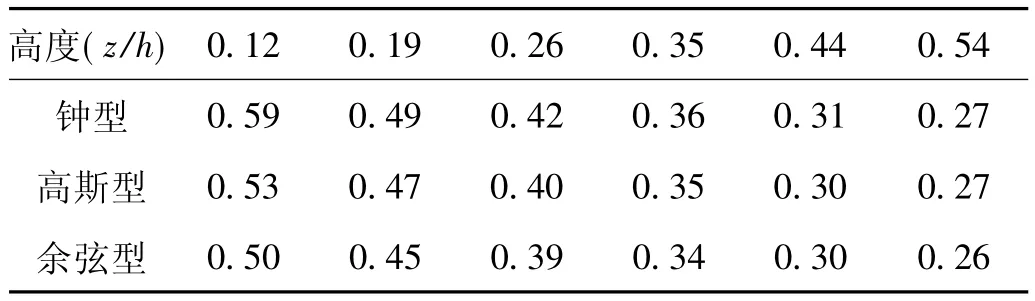
表2 不同山体形状山顶加速比对比Tab.2 The comparison of speed-up ratio at the hilltop of different hill shapes
2.4 山顶加速比沿高度的分布
综合前面的分析,可以看出加速比沿高度的分布可以归纳为两种形式:一种是以美国规范为代表的指数函数形式;一种是以澳大利亚规范为代表的反函数形式。取较缓和较陡两种坡度,分别运用公式(14a)和(14b)对山顶平均风加速比数值计算的结果进行拟合,如图5所示。

式中ΔSmax反映的山顶表面的最大加速比,而k反映的是加速比的影响高度。
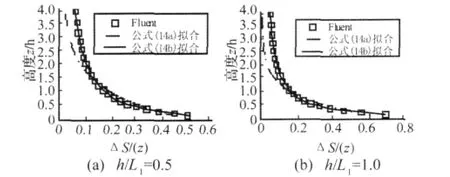
图4 数值模拟结果的拟合Fig.4 The fitting of the numerical simulation result
可见,不管坡度是缓还是陡,用反函数的形式进行拟合的结果与数值模拟吻合更好。因此,本文都采用反函数的形式进行拟合。
2.5 山体坡度影响
由澳大利亚规范可得:
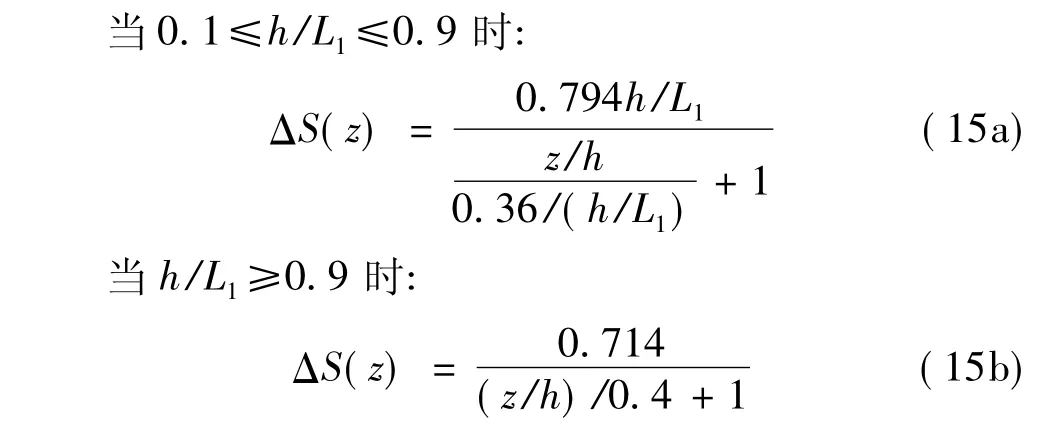
可以看出澳大利亚规范中ΔSmax随山体坡度线性增加,一直到坡度为0.9时趋于0.714,而k与山体坡度呈反函数关系,最后趋于0.4 H。
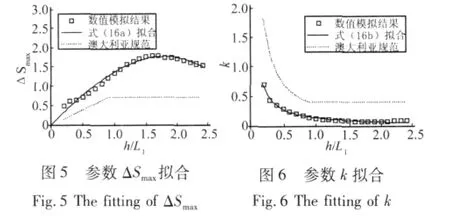
对不同坡度下山顶加速比数值模拟数据进行参数ΔSmax和k二次拟合的结果可见图5、图6。
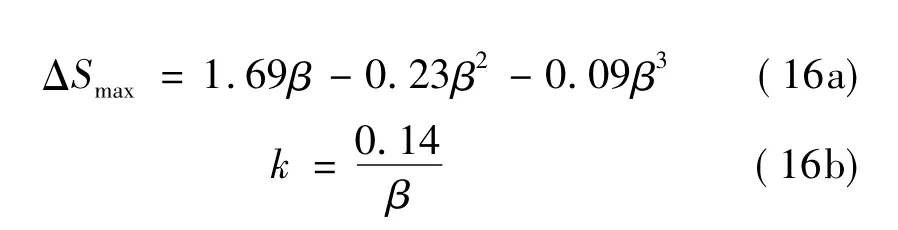
其中坡度β=H/LH。
由图6可见,参数k用式(16b)拟合的结果与计算结果非常吻合,但与澳大利亚规范相比,明显要小。
2.6 湍流特征
湍流的强弱主要由湍动能来衡量。类比于平均风速,山地风场湍动能的改变也可以用湍动能增大系数来表示,如公式(17)所示。
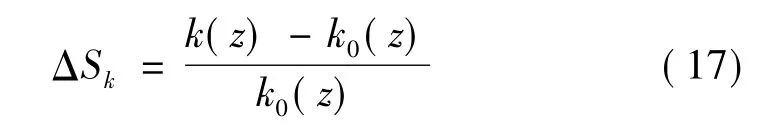
由图6可见,与澳大利亚规范相比,参数ΔSmax数值模拟和拟合结果比规范要大,同时曲线形状也有所不同。规范采用的是折线形模型,而计算结果可以用经过原点的三次多项式如式(16a)拟合,拟合效果很好。
式中:k(z)表示山地地面以上z高度处的湍动能,k0(z)表示平地地面以上z高度处的湍动能。
由图可以看出,当坡度较小时,山顶近地湍动能比来流湍动能略小,分析原因可能是数值模拟大气边界层的不平衡原因引起的。对于这个问题,很多学者进行了研究[23],但是有效的保持大气边界层水平平衡性,尤其是近地表水平平衡性的方法还没有得到。
随着坡度增大,底部湍动能逐渐增大,但增大并不明显。而边界层上部湍动能却略有减小,分析原因应该为上部边界层基本没有受到山地的干扰,因此如果以绝对高度来比较,应该是相等的,但是增大系数是以相对于地表的高度来比较的,而湍流度随高度越高而约小,因此上部边界层湍动能增大系数还略有减小。总的来说,山顶湍动能的变化不大,没有平均风速的增大效应明显。
3 山地风场风洞试验对比
试验在中国空气动力研究与发展中心低速所1.4 m×1.4 m风洞中进行。几何模型缩尺比为1∶1 000,风速缩尺比约为1∶2.5,测试仪器采用排管和电子扫描阀。对大气边界层进行了细致的调试,评价指标包括平均风速剖面、湍流度剖面、脉动风功率谱、各指标均满足要求。试验湍流积分尺度结果约为0.2m,换算到实际尺度约200 m,与大气边界层的湍流积分尺度基本一致。
山体坡度分别为0.5和1.0时,山顶平均风加速比数值模拟和试验的对比见图8。
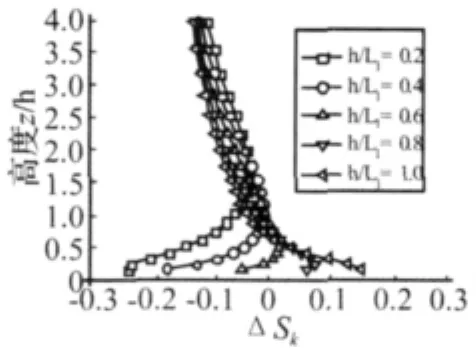
图7 湍动能增大系数Fig.7 Increasing coefficient of turbulent kinetic energy
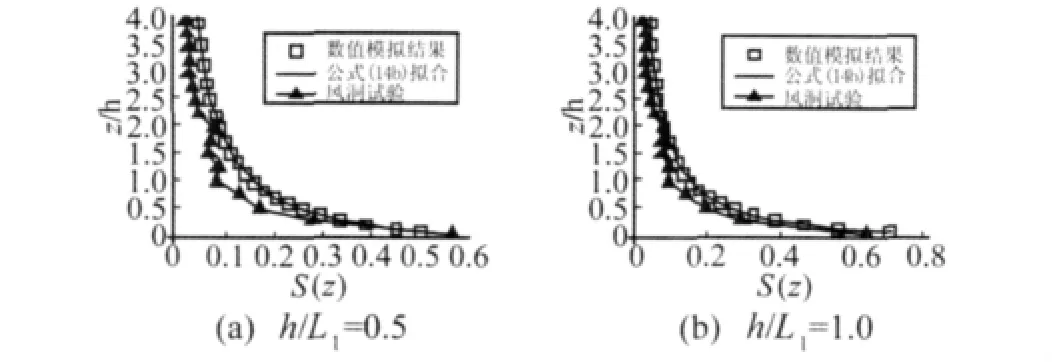
图8 平均风加速比数值模拟和风洞试验对比Fig.8 Comparison of the speed-up ratio
由图8可知,不管较缓的山体还是陡峭的山体,数值模拟和风洞试验的结果都非常接近,数值模拟的结果略大,加速比沿高度的分布基本相同。数值模拟在平均风速风压的模拟方面已经比较准确。本文拟合的山地平均风加速比公式为对山地平均风取值提供了参考。
但是从许多学者进行数值模拟的经验来看,风场湍流模拟方面与试验相比还有一定差距。以下列出本文数值模拟与风洞试验湍动能的对比,如图9。
由湍动能增大系数对比可以看出,数值模拟和风洞试验结果基本都分布在-0.2~0.2之间,在边界层上部比较吻合,但是在近地部分有较大差别。数值模拟比风洞试验在近地高处湍动能要高,估计与模拟采用的湍流模型有关,两参数的高雷诺数湍流模型都过大的估计了近地处的湍动能。因此,数值模拟的结果比试验要高。
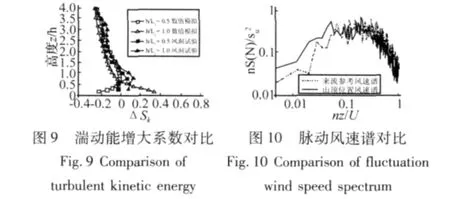
由于数值模拟采用的定常计算,并不能反映风场的频域特性,因此山地风场的频域特性只能通过风洞试验得到。为此将风洞试验中,山顶位置脉动风速功率谱与前方来流参考脉动风速功率谱进行对比如图10。
由图可见,山顶位置纵向脉动风速功率谱与来流脉动风速基本一致。山顶位置与平地相比,频域特征基本相同。
4 山地风场下超高层建筑风振响应分析
某超高层建筑总高300 m,特征宽度50 m,高宽比为6.0,单位高度质量5×105kg/m。由于超高层建筑各频率间隔较大,振型间的耦合影响较小,同时高阶振型影响较小,因此本文仅计算超高层建筑的一阶位移响应。一阶振型取为线性振型,一阶频率0.15 Hz,周期约为7 s,阻尼比1.5%,基本风压取为0.55 kPa。通过抖振频域分析方法计算建筑的风振响应,以得到山地对超高层建筑风振响应的影响范围
由数值模拟和风洞试验的结果可知,山顶位置风场的湍流特性和频域特性变化不大,因此本文平地和山顶位置的风速谱均直接选用广泛应用的Davenport谱,见公式(19);相干函数采用指数形式,如公式(20),取Cy=7。
则一阶广义力谱可由各层荷载互谱乘以振型的平方在空间上积分得到,如公式(21);

一阶广义力谱乘以传递函数就得到一阶广义位移谱,然后再乘以振型的平方就可以得到各层位移谱,如公式(22);
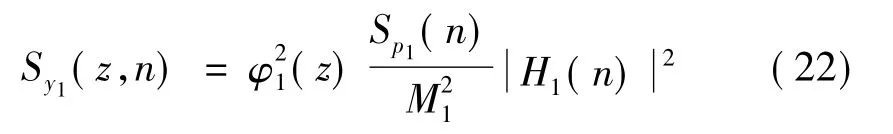
对各层位移谱频域积分可得各层位移根方差值,如公式(23);再乘以峰值系数3.0,叠加上平均静力响应,即可得到超高层建筑的总响应。

表3 平地与山地高层1建筑顶部位移响应对比Tab.3 Displacement response of building in flat terrain and in hilly terrain
平地超高层建筑和坡度为0.5的山顶位置超高层建筑风振响应对比见表3,由表3可见,当超高层建筑位于坡度为0.5的山地的山顶时,超高层建筑的平均位移响应、动力位移响应以及总位移响应都比相应的平地要大。其中平均位移响应增大约28%,动力位移响应增大约20%,总的位移响应增大24%。
虽然山体坡度越大,近地风场平均风加速比越大,但是影响的高度也越小。因此坡度越大,对超高层建筑的影响并不一定一直增大,会存在一个极值坡度。与平地情况相比,将不同坡度下超高层建筑的顶部位移风振响应放大系数计算如图11所示。
由图11可见,对于算例特定的超高层建筑而言,按美国规范的公式,超高层建筑的顶部位移响应在坡度为0.2时达到最大,与平地相比顶部位移放大系数达到1.3。按澳大利亚规范计算顶部位移放大系数随坡度增大而增大,直到坡度为0.9时趋于平稳,最大达1.25。按数值模拟结果计算的顶部位移响应在山体坡度为0.7时达到最大,顶部位移放大系数1.2。如果把澳大利亚规范在坡度大于0.9的部分可以看作是保守的归并,那么数值模拟的极值坡度正好在美国规范和澳大利亚规范之间。

图11 不同坡度建筑顶部位移放大系数Fig.11 Displacement increasing coefficient by different slope
5 结论
由数值模拟的分析,以及和风洞试验的对比可以得出以下结论:
(1)山地对平均风有较大的增大效应,山顶位置最大加速比可达1.7,对维护结构的计算要严加考虑。
(2)山顶平均风最大加速比先增大后减小,而影响高度系数随坡度增大呈反函数减小。本文拟合的山地平均风加速比公式为山地平均风取值提供了参考。
(3)数值模拟和风洞试验的对比可以看出,平均风的模拟有较高准确性,湍流模拟与试验结果相比还有一定差距。
(4)通过某超高层建筑的风振响应分析表明,山地风的增大效应对结构整体响应计算不可忽略,位移响应增大比例最大可达20%。
[1]Taylor P A,Mason P J,Bradley E F.Boundary-layer flow over low hills-A review[J].Boundary-Layer Met,1987,39:107-132.
[2]Taylor P A.Turbulent boundary-layer flow over low and moderate slope hills[J].Journal of Wind Engineering and Industrial Aerodynamics,1998,74 -76;25 -47.
[3] Miller C A,Davenport A G.Guidelines for the calculation of wind speed-ups in complex terrain.JournalofWind Engineering and Industrial Aerodynamics 74-76(1998)189-197.
[4]Weng W,Taylor P A,Walmsley J L.Guidelines for airflow over complex terrain:model developments.Journal of Wind Engineering and Industrial Aerodynamics, 2000, 86:169-186.
[5] Kim H G,Patela V C,Leeb C M.Numerical simulation of wind flow over hilly terrain.Journal of Wind Engineering and Industrial Aerodynamics,2000,87:45 -60.
[6] Kim H G,Lee C M,Lim H C,et al.An experimental and numerical study on the flow over two-dimensional hills.Journal of Wind Engineering and Industrial Aerodynamics,1997 ,66:17-33.
[7]Carpenter P,Locke N .Investigation of wind speeds over multiple two-dimensional hills.Journal of Wind Engineering and Industrial Aerodynamics,1999,83:109 -120.
[8] Takahashi T,Ohtsu T,Yassin M F,et al.Turbulence characteristics of wind over a hill with a rough surface.Journal of Wind Engineering and Industrial Aerodynamics,2002,90:1697-1706.
[9]Jackson P S,Hunt J C R.Turbulent wind flow over a low hill[J].Q.J.Roy.Meteorol.Soc,1975,101:929 -955.
[10] Jackson P S.The influence of local terrain features on the site selection for wind energy generating systems[R].Boundary Layer Wind Tunnel Laboratory Internal Report,University of Western Ontario,BLWT -1 -1979,1979.
[11] Hunt J C R,Leibovich S,Richards K J.Turbulent shear flow over low hills[J].Q.J.Roy.Meteorol.Soc,1988,114:1435-1470.
[12] Mason P,Sykes R.Flow over an isolated hill of moderate slope[J].Q.J.Roy.Meteorol.Soc,1979,105:383 -395.
[13] Kaimal J,Finnigan J.Atmospheric Boundary Layer Flows-Their Structure and Measurement[M].Oxford,Oxford University Press,Oxford,1994.
[14] Taylor P A,Lee R J.Simple guidelines for estimating wind speed variations due to small scale topographic features[J].Climatol.Bull,1984,18(2):3 -22.
[15]中华人民共和国国家规范.建筑结构荷载规范(GB50009-2006)[S].北京:中国建筑工业出版社,2006.
[16] ANSI/ASCE Standard,Minimum Design Loads for Buildings and Other Structures,2002[S].
[17] National Commission of Building and Fire Code[S],National Building Code of Canada 1995(NBC),National Research Council of Canada,1995.
[18] International Standard ISO4354.Wind Actions on Structures[s],2004.
[19] AIJ Recommendations for Loads on Buildings.Architectural Institute of Japan,2004[s].
[20] AS/NZS 1170.2:2002.Australian/New Zealand Standard,Structural design actions,Part 2:Wind actions[s].
[21] Blocken B,Stathopoulos T,Carmeliet J.CFD simulation of the atmospheric boundary layer:wall function problems.Atmos.Environ,2007,41(2),238 -252.
[22] Fluent Inc.Fluent 6.3 User’Guide.Fluent Inc.,Lebanon,2006.
[23] Richards P J,Hoxey R P.Appropriate boundary conditions for computational wind engineering models using the k-e turbulence model.J. Wind Eng.Ind. Aerodyn,1993,46&47,145-153.
Wind-induced response of super tall buildings in hilly terrain
LI Zheng-liang1,WEI Qi-ke1,HUANG Han-jie2,SUN Yi1
(1.College of Civil Engineering,Chongqing University,Chongqing 400045,China;2.China Aerodynamics Research& Development Center,Mianyang 621000,China)
Considerable changes of amplitude and spatial distribution of wind velocity take place under interfering of hilly terrain.Wind load and response of super tall buildings at special locations in hilly terrain are significantly different from those in flat terrain,therefore,the current methods for calculating wind-induced response of super tall buildings in flat terrain may be unsafe under condition of hilly terrain.Previous studies were mainly focused on mean wind speed-up effect,and very few studies on turbulent characteristic of pulsive wind are involved with this subject.Besides,there is no comparison between results of wind induced response of super tall buildings in hilly terrain and those in flat terrain.Herein,several kinds of 3D hill model including bell,Gaussian and cosine shaped ones were established with CFD software Fluent.Vertical profiles of mean wind velocity at crest were calculated under different hill slopes.The numerical simulation showed that the great speed-up effect is found at crest and the maximum speed-up ratio reaches 1.7;the results with those using inverse functions;compared to the test data,the simulation of mean velocity is accurate,but the numerical simulation of turbulent has a certain difference.A numerical example of wind-induced response of a super-tall building showed that the effect of hilly terrain can't be ignored,and its displacement response in hilly terrain increases 20%compared with that in flat terrain.
hilly terrain wind field;CFD;wind tunnel test;super tall buildings;wind-induced response
TU973+.31
A
国家自然科学基金重大研究计划(90715024)
2010-02-05 修改稿收到日期:2010-03-01
李正良 男,教授,博士生导师,1963年生

