空间绳系系统自由展开建模与仿真
孔宪仁,徐大富,杨正贤,王本利
(哈尔滨工业大学 卫星技术研究所,哈尔滨 150001)
空间绳系系统自由展开建模与仿真
孔宪仁,徐大富,杨正贤,王本利
(哈尔滨工业大学 卫星技术研究所,哈尔滨 150001)
运用Hamilton原理建立了空间绳系展开动力学模型,研究绳系展开过程中绕线盘出线、系绳振动以及末端质量的运动规律,并利用中心差分法、四阶Runge-Kutta和预估校正法等数值方法对绳系的自由展开过程进行仿真,仿真结果显示该模型可以较精确描述绳系系统在展开过程中的复杂非线性动力学行为,绳系自由展开不能满足稳定展开的要求,仿真数据可以为后续的绳系展开控制提供参考依据。
空间绳系展开;动力学模型;自由展开;中心差分法;非线性动力学
空间绳系系统是指利用柔性系绳将两个或两个以上的航天器连接在一起所构成的空间飞行系统。绳系连接的航天器可以是小型的探测器、卫星、飞船、航天飞机、空间站等等,甚至可以是废弃的运载火箭上面级。空间绳系系统具有广阔的潜在应用前景,文献中所涉及的应用[1-15]主要有:航天器轨道转移与升降、绳系星座与编队、电动力绳系离轨、绳系交会、绳系人造重力、空间站轨道保持、绳系推进的行星际航行、绳系太阳帆等等。
对于空间绳系系统,系绳的顺利展开是完成空间任务的先决条件,1996年的 TSS-1R和1998年的ATEx两次空间绳系实验都因为绳系展开故障而导致整个计划失败。绳系展开的动力学使用不同方法和模型进行描述,文献[16,17]中绳系作为无质量的刚体,不考虑系绳所受的重力、惯性力和张力,这个模型是最简单最基本的模型,可用来研究两个质点用定长的系绳连接后在重力和惯性力下的运动情况。文献[18,19]将绳系作为有质量的刚体,考虑作用在系绳上的重力梯度力和惯性力影响,但是忽略了系绳中的张力。文献[20]中绳系作为无质量的柔性体,考虑张力影响,但是忽略其他力的影响。文献[21-24]中绳系被模化为一系列集中质量点,之间通过无质量的弹簧连接,该模型也称为珠链模型,可以描述弹性系统的动力学问题。文献[25]提出了三种绳系模型,研究了绳系展开和回收的动力学与控制问题,根据牛顿定律和弹性力学原理推导绳系动力学方程,利用Ritz方法假设3个振型函数将偏微分方程转换成常微分方程,并使用Matlab中ODE算法进行数值求解。
本文运用Hamilton原理建立了绳系展开动力学方程,研究绳系展开过程中绕线盘出线、系绳振动以及末端质量的运动规律,并利用中心差分法、四阶Runge-Kutta和预估校正法等数值方法对绳系的自由展开过程进行仿真,为以后的绳系展开控制提供参考依据。
1 绳系展开的动力学模型
绳系系统由卫星本体ms、末端质量mB和已展开部分的绳索(未展开的部分缠绕在绕线盘上,处于卫星本体中),如图1所示。假设s表示绳索无伸展时的弧长,s变化范围是从0到绳索全长L,假设表示绳索瞬时构型的弧长,末端质量处=L,绳索离开绕线盘处=ξ(t),该点既在绳索上也在绕线盘上,使用=ξ+(t)表示该点仅在绳索上,绳索和绕线盘固联的部分=0。选取在处的绳索单元,该微元在惯性坐标系下的位置矢量rt(,t),满足关系rt(,t)=R0er+r(,t),其中r(,t)表示该微元相对于卫星的位置矢量,R0表示卫星轨道半径。rt和r既与绳索瞬时弧长的位置有关,又与时间t相关,所以可以表示为rt(,t),r(,t),为推导公式时方便,仍记为rt和r。同时rt(L,t)可以简记为rtL,ξ(t)记为 ξ。
整个系统的动能包括:已展开部分绳索的动能、末端质量的动能、卫星本体和未展开部分绳索的动能、绕线盘和未展开部分绳索的转动动能,即:
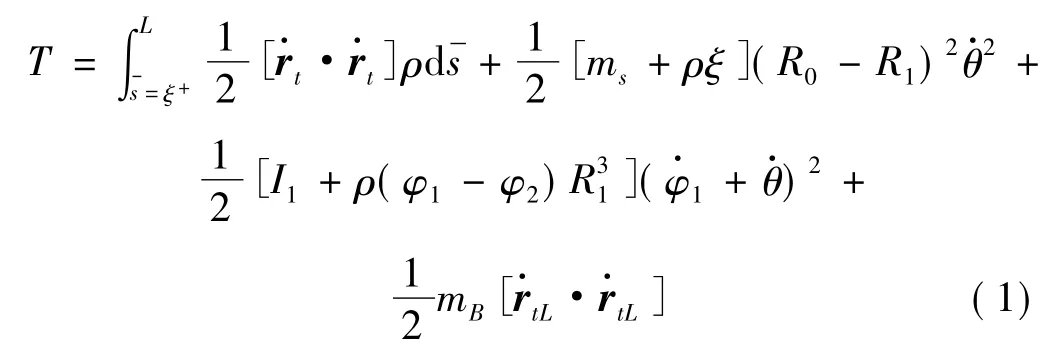
其中,ρ表示系绳的线密度,R1表示绕线盘的半径,I1表示绕线盘的惯性矩。
系统的势能包括:卫星本体和未展开部分绳索的重力势能、末端质量的重力势能、已展开部分绳索的重力势能、已展开部分绳索的弹性势能,即:

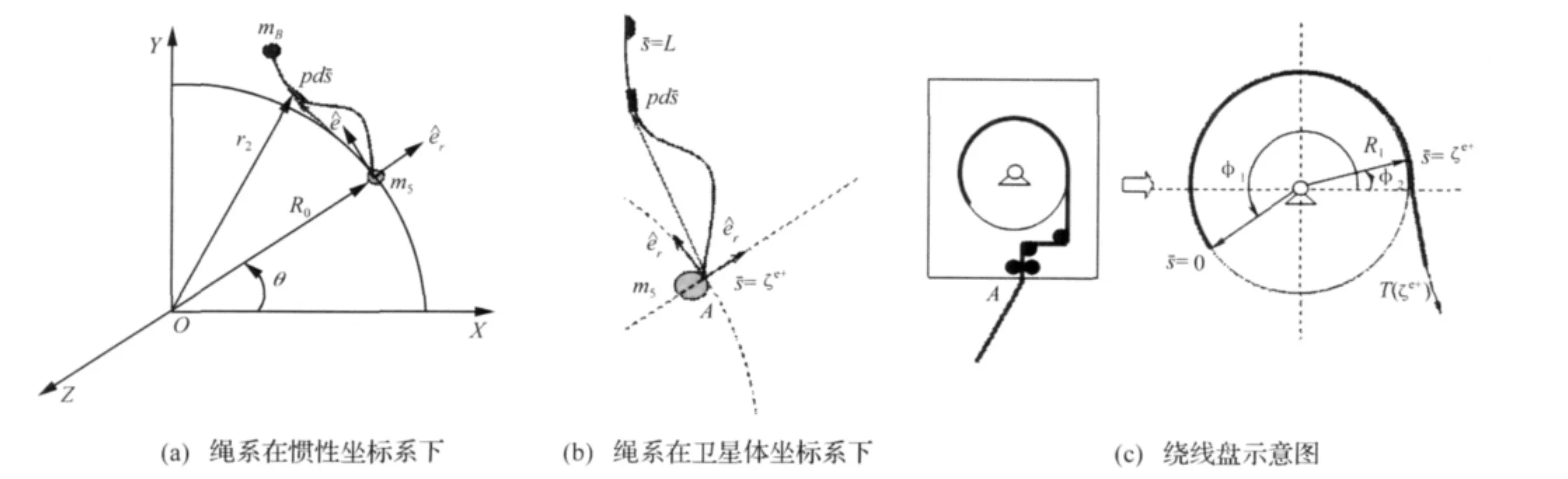
图1 空间绳系展开过程示意图Fig.1 Schematic of space tether deployed in orbit


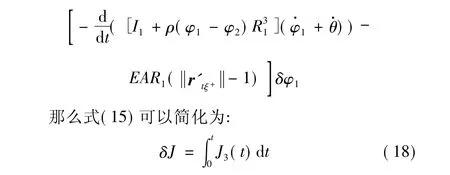
绳系展开时,主要控制力为末端球体上推力器的作用力F以及绳系绕线盘上提供的摩擦力矩τ,则控制绳索展开外力所作的虚功为 δW=F·δrtL+τδφ1,绳索的拉力在=ξ处是不连续的,可以视为虚拟的激励,表示为Timp,它的虚功表示为Timpδξ。总的虚功表示为:

绳索展开时,绳索离开绕线盘的过程是连续的,假设开始展开时其方向也是确定的,选择φ2=0并且=0,则方程(22)可以变为:
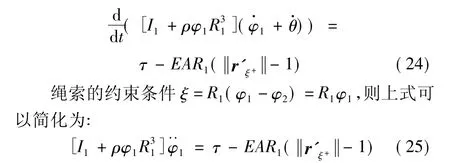
方程(20)、(21)、(25)即为绳系展开的动力学方程,其中方程(20)描述绳系已展开部分的运动,方程(21)描述末端质量的运动情况,方程(25)绕线盘上绳系展开的动力学特性。



方程(33)至(39)分别描述了系绳、末端质量、绕线盘在展开过程中的复杂的非线性动力学行为,假设末端球体上推力器的作用力F以及绳系绕线盘上提供的摩擦力矩τ都为零,绳系进入无控的自由展开状态。
2 仿真验证
绳系实际展开过程中一般需要利用末端球体上推力器的作用力F以及绳系绕线盘上提供的摩擦力矩τ对展开过程进行控制,无控制的自由展开在空间任务中并不采用。本文无控制的自由展开仿真目的是研究绳系在展开过程中的运动规律,为以后的控制策略选择提供依据。
方程(33)至(39)中包含时间t和空间位置(x,y,z)的导数,对于这类二阶非线性、时变、强耦合的偏微分方程,无法求出解析解,可以利用中心差分法进行时间和空间上的离散,建立离散化方程,然后结合四阶Runge-Kutta和预估校正法等数值方法进行求解。
系绳为铝质的多股编织绳,横截面直径为1 mm,弹性模量为72 GPa。绕线盘直径为242 mm,围绕转轴的转动惯量为4 kg·m2。末端质量重30 kg。假设卫星在距离地面600 km高的圆轨道上展开绳系,绳系首先使用弹射的方法展开最初的100 m长度,为后续的展开提供足够的梯度力,自由展开过程从已经展开的100 m长度开始。
仿真结果如图所示,图2表示在卫星体坐标系下绳系展开过程,绳系沿径向向上展开,绳系长度增加的同时,也向后上方偏转。绳系初始展开时不包含引起面外运动的速度分量,所以绳系的运动都在er—eθ平面内。图3表示展开过程中绳系张力的变化情况,末端质量处(=L)的张力与绳索离开绕线盘处(=ξ)的张力变化趋势一致,随着系绳展开长度的增加,张力也增加,这是因为作用在绳系上的梯度力随着绳长增加。图4表示绳长的变化,随着时间增加,系绳的展开速度越来越快。绕线盘出线速度与=ξ处张力直接相关,张力越大出线速度越快。当绕线盘出线速度超过末端质量带动系绳的运动速度时,系绳可能会因为局部松弛引起缠绕。
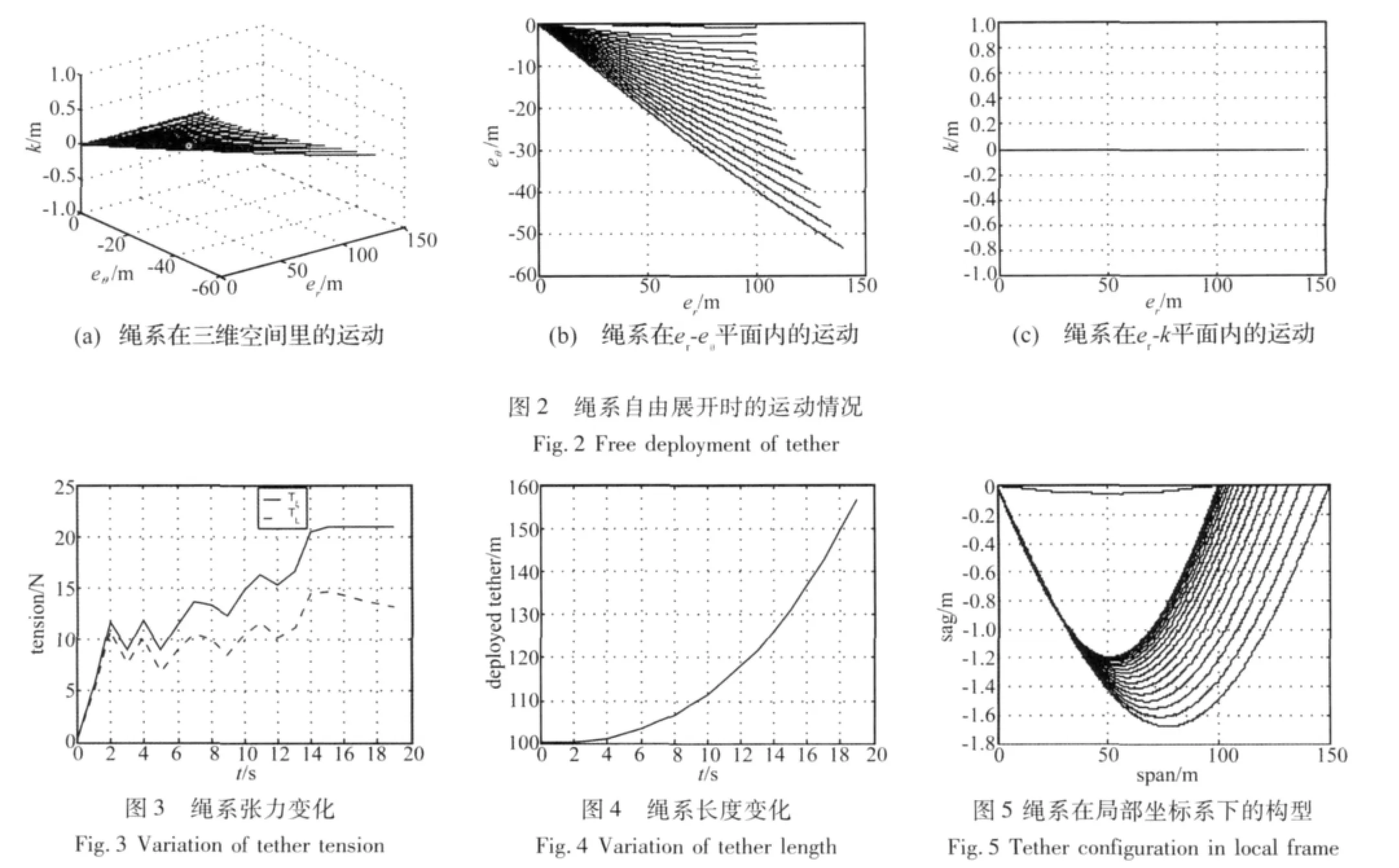
为更直观地研究展开过程中系绳的运动情况,建立一个局部坐标系,该坐标系以绕线盘出线点为原点,以绕线盘出线点和末端质量质心的连线为x轴,正方向径向向外,y轴在er-eθ平面内与其垂直,正方向与卫星运动方向成锐角。x轴与y轴实际上表示系绳的跨度和垂度。将绳系在空间内的运动通过坐标转换变换到局部坐标系下,结果如图5所示。随着时间变化,展开的绳系长度不断增加,系绳在空间的垂度和跨度也相应增加,横向与纵向振动加剧。
3 结论
运用Hamilton原理建立了绳系展开动力学模型,仿真结果显示了绳系自由展开过程中绕线盘出线、系绳振动以及末端质量的运动规律。该模型使用二阶非线性、时变、强耦合的偏微分方程描述运动规律,比其他模型更能准确表现绳系的自然特性,但是要注意的是数值仿真时计算量非常大。
绳系自由展开时,系绳张力增大会导致绕线盘出线速度加快,当出线速度超过末端质量带动系绳运动速度时,已展开的系绳容易出现缠绕现象,需要绕线盘上提供的摩擦力矩τ对出线速度进行控制。另外,系绳自由展开时会偏离径向方向,甚至会产生面外运动,需要末端球体上推力器的作用力F对其运动进行控制。绳系自由展开不能满足稳定展开的要求,选择合适的控制策略对展开过程进行控制,使绳系以稳定的速度展开,同时系绳中保持合适的张力避免松弛引起缠绕,这是下一步需要研究的内容。
[1] Lorenzini E C,Cosmo M L,Kaiser M,et al.Mission analysis of spinning systems for transfer from low orbits to geostationary[M]. Harvard-Smithsonian Center for Astrophysics;1999[preprint series no 4803].
[2]Hoyt R P,Forward R L.Tether transport from sub-Earth orbit to the lunar surface and back! [C].In:Proceedings of the international space development conference,Orlando,May 1997.
[3]Cartmell M P,Ziegler S W,Neill D S.On the performance prediction and scale modelling of a motorised momentum exchange propulsion tether[C].In:Proceedings of the STAIF2003 conference.University of New Mexico,2003.
[4] Bekey I.Tethers open new space options[J].Astronaut Aeronaut,1983;21(4):32 -40.
[5] Carroll J A.Tether applications in space transportation[J].Acta Astronaut 1986;13(4):165-174.
[6]Moravec H.A nonsynchronous orbital skyhook[J].J Astronaut Sci 1977;25(4):307-322.
[7]orward R L.Tether transport from LEO to the lunar surface[C].In:Proceedings of the 27th AIAA/ASME/SAE/ASEE joint propulsion conference and exhibit.AIAA; 1991:91-2322.
[8]Bernelli-Zazzera F.Active control of tether satellites via boom rotation:a proof of concept experiment[C].In:Proceedings of THE AAS/AIAA space flight mechanics meeting,p.1225 40[AAS.01-192].
[9]McInnes C R,Cartmell M P.Propellantless propulsion.In:Modern astrodynamics[M].vol.1.Elsevier Astrodynamics Series.Oxford,Amsterdam:Elsevier Academic Press,2006.
[10] Ziegler SW,Cartmell MP. Using motorised tethers for payload orbital transfer[J].J Spacecraft Rockets,2001;38(6):904-913.
[11] McKenzie D J, Cartmell M P. Large tether and web structures in space.In:Symposium on the mechanics of slender structures,University of Northampton& Institute of Physics,28 29 September 2006. CD-ROM paper under authors'names[J].ARTICLE IN PRESS M.P.Cartmell,D.J. McKenzie /Progress in Aerospace Sciences,2008,44(18):1-2.
[12] McKenzie D J.The dynamics of large space structures:tethers on an inclined orbit,deployment of tethers,and space webs[D].Department of Mechanical Engineering,University of Glasgow,2007.
[13] Forward R L,Hoyt R P.Space tethers[J].Sci Am,1999:86-87.
[14]Cartmell M P,Ziegler S W.Symmetrically laden motorised tethers for continuous two-way interplanetary payload exchange[C].In:Proceedings of the 35th AIAA/ASME/SAE/ASEE joint propulsion conference and exhibit,AIAA,1999[AIAA 1999-2840].
[15] Rauwolf G A,Pelaccio D G,Patel S,et al. Mission performance of emerging in-space propulsion concepts for oneyear crewed Mars missions[C].In:Proceedings of 37th AIAA/ASME/SAE/ASEE joint propulsion conference and exhibit,AIAA[AIAA 2001- 3374].
[16]Bae G,Sim E,Barlow J B.Dynamics of a tethered satellite system[J].Advances in the Astronautical Sciences,1993,82(2):1297-1310.
[17] BreakwellJV,GearhartJ W. Pumping a tethered configuration to boost its orbit around an oblate planet[J].Journal of the Astronautical Sciences,1987,35(1):19 -39.
[18] Mankala K K,Agrawal S K.Equilibrium to equilibrium maneuvers of rigid electrodynamic tethers[J].Journal of Guidance,Control and Dynamics,2005,128(3):541 -545.
[19] Pelaez J,Lopez-Rebollal O,Lara M,et al.Dynamic stability of a bare tether as a deorbiting device[J].In Advances in the AstronauticalSciences, volume 112 II, pages,2002:1257-1274.
[20] Kumar K D,Yasaka T.Rotating formation flying of three satellites using tethers[J]. JournalofSpacecraftand Rockets,2004,41(6):973 -985.
[21] Banerjee A K. Dynamics oftethered payloads with deployment rate control[J].Journal of Guidance,Control and Dynamics,1990,13(4):759 -762.
[22]Greene M,Glawtney D A. Preliminaryinvestigation of dynamic control of a single tethered satellite system using a tether crawler[J].In Proceedings of the Annual Southeastern Symposium on System Theory,Tallahassee,FL,USA,1989:173-177.
[23] Kim E,Vadali S R.Modeling issues related to retrieval of flexible tethered satellite systems[J].Journal of Guidance,Control,and Dynamics,1995,18(5):1169 1176.
[24] Le D K.Modeling of a tethered two-body system in space[J].Simulation Series,1986,16(2):86 97.
[25]Mankala K K,AgrawalSK. Dynamicmodelingand simulation of satellite tethered systems[J].Journal of Vibration and Acoustics,2005,127(2):144 -156.
Modeling and simulation for free deployment of a space tether system
KONG Xian-ren,XU Da-fu,YANG Zheng-xian,WANG Ben-li
(Research Center of Satellite Technology,Harbin Institute of Technology,Harbin 150001,China)
A dynamic model of space tether deployment was established using Hamilton’s principle to study motion laws of drum releasing tether,tether vibration and end-mass moving during tether deployment.Numerical simulation for free tether deployment was calculated using central difference method,four-order Runge-Kutta method and predictorcorrector method and so on.The simulation results showed that the model can accurately describe the complex nonlinear dynamic behavior of a space tether system during deployment;free deployment cannot meet requirements of stable tether deployment,but the simulation data provide a foundation for tether deployment control further.
space tether deployment;dynamic model;free deployment;central difference method;nonlinear dynamics
V524.3
A
长江学者和创新团队发展计划资助(IRT0520)
2009-12-24 修改稿收到日期:2010-03-10
孔宪仁 男,教授,博士生导师,1961年生

