潜孔钻头柱齿和齿孔过盈配合的弹塑性有限元分析

王琳

（天水风动机械有限公司技术中心，甘肃天水741020）

冲击旋转凿岩是将冲击破岩和刮削破岩两种方式结合在一起的钻凿技术。该技术所用钻压和扭矩小，不容易发生孔斜，作为解决常规凿岩方式在硬岩地层段钻进速度慢、效率低的有效方法之一，在潜孔钻凿领域得到了越来越广泛的应用。

1 问题的提出

潜孔钻头是实施冲击旋转凿岩的专用钻头，笔者在对青海木里煤矿和甘肃柳园甘新高铁施工段潜孔钻头应用情况调查发现，现场用的Q13115-H64型潜孔钻头在钻进过程中常常发生柱齿脱落、折断和破碎、岩屑排除不畅等问题，严重制约了冲击旋转凿岩效率。文献[1]对Q13115-H64型潜孔钻头进行了井底流场分析，改进了其水力结构参数，解决了排屑不畅的问题，但柱齿脱落、折断等问题还没有得到圆满的解决。

在冲击旋转钻进过程中，钻头要受到很大的冲击载荷作用，柱齿与钻头本体通过过盈配合联接在一起，冲击载荷通过柱齿传到钻头本体上。因此，过盈量过小的选择，直接关系到潜孔钻头的破岩效果与使用寿命，分析钻头齿孔过盈配合产生的应力场分布规律，对过盈量的选取以及钻头几何尺寸设计和强度设计，都具有十分重要的意义。

潜孔钻头的过盈量通常在十几到几十微米范围内变动，不同型号的钻头，其过盈量是不同的。如果采用试验的方法来确定，需要进行一系列的重复试验，周期长，代价高，其精度受到试验设备及测试技术等多种因素的影响。文献[2]中采用有限元法对柱齿与齿孔的过盈配合问题进行了详细的研究，提出了很有价值的观点，但分析都是基于对单齿或多齿过盈配合的研究，而不是针对完整钻头的过盈配合研究，不能准确地反映钻头本体的应力分布情况。本文以Q13115-H64型潜孔钻头为原型，利用有限元分析软件ANSYS10.0对不同过盈量下钻头本体的应力分布规律进行了详细的研究。

2 有限元分析的理论与方法

在ANSYS10.0中直接建模。齿孔过盈量一般是在十几到几十微米的范围内变动，从力学角度来看，这种几何变形会引起钎头本体刚度的改变，属于大应变非线性问题。另外，由于柱齿的嵌入，当过盈量达到某一数值时，将使齿孔局部区域发生塑性变形，而远离孔壁的区域又处于弹性状态，出现了弹塑性共存的局面，属于材料非线性问题。

在通常情况下，柱齿由硬质合金制成，其弹性模量比本体材料大一个数量级，甚至大两个数量级。可以认为，在同等条件下的变形也是相差数量级的。因此，在误差允许的范围之内，将硬度极大、变形极小的柱齿视为不变形的刚性体，这样柱齿与齿孔配合的过程中，过盈量全部均匀作用在孔壁上，此时的齿孔边界变形可以认为是大应变非线性和材料非线性的双重非线性问题。

对于非线性问题，增量形式的有限元控制方程为

式中{K}——增量刚度矩阵

{△U}——增量位移矩阵

{F}——节点等效力向量

3 潜孔钻头本体弹塑性静力分析模型

3.1 有限元分析模型

Q13115-H64型潜孔钻头虽然体积不大，但由于凿岩的特殊要求，其结构形状比较复杂，这就使得在建立有限元模型时需要对模型进行适当的简化。有限元分析主要考察柱齿过盈量在钻头本体上产生的应力分布情况，因此，分析模型取潜孔钻头头部结构作为研究对象，忽略潜孔钻头的冲击端面和花键等结构。采用积分二次四面体Solid92单元对模型进行网格划分，并对齿孔周围应力变化较大的地方进行局部网格加密，得到如图1所示的潜孔钻头网格模型。

图1 Q13115-H64潜孔钻头网格模型

3.2 边界条件的处理

根据前面的理论分析，全部过盈量均匀施加在齿孔内壁上，以此来近似模拟齿孔的过盈配合。钻头头部结构的下表面（图2所示A面）与钻头花键（图2所示B处）相连，根据圣维南原理，该表面远离齿孔，对齿孔的应力分布影响不大，取模型下表面全部为零位移边界条件，从而有了约束条件。

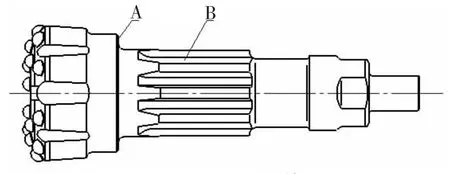
图2 Q13115-H64潜孔钻头外形图

3.3 材料的本构关系

塑性材料的本构关系一般以拉伸的应力应变曲线形式给出。材料数据可能是工程应力（σ＝P/A0，P为载荷，A0为试样的原始截面积）与工程应变（ε＝（L-L0）/L0，L为试样变形后的长度，L0为试样的原始标距长度），也可能是真实应力（P/A，P为载荷，A为受载后实际的截面面积）与真实应变（瞬时伸长量除以瞬时长度）。因为真实应力、真实应变可以排除工程应力、工程应变中达到最大值后应力-应变曲线出现应力下降的假象，因此大应变的弹塑性分析一般采用真实应力、真实应变数据，而小应变分析一般采用工程的应力、应变数据。钻头本体材料选用20Ni4Mn(经调质处理)，其弹性模量E=2.18×105MPa，泊松比μ=0.3，真实应力应变关系采用如图3所示的折线来拟合。

4 计算结果分析

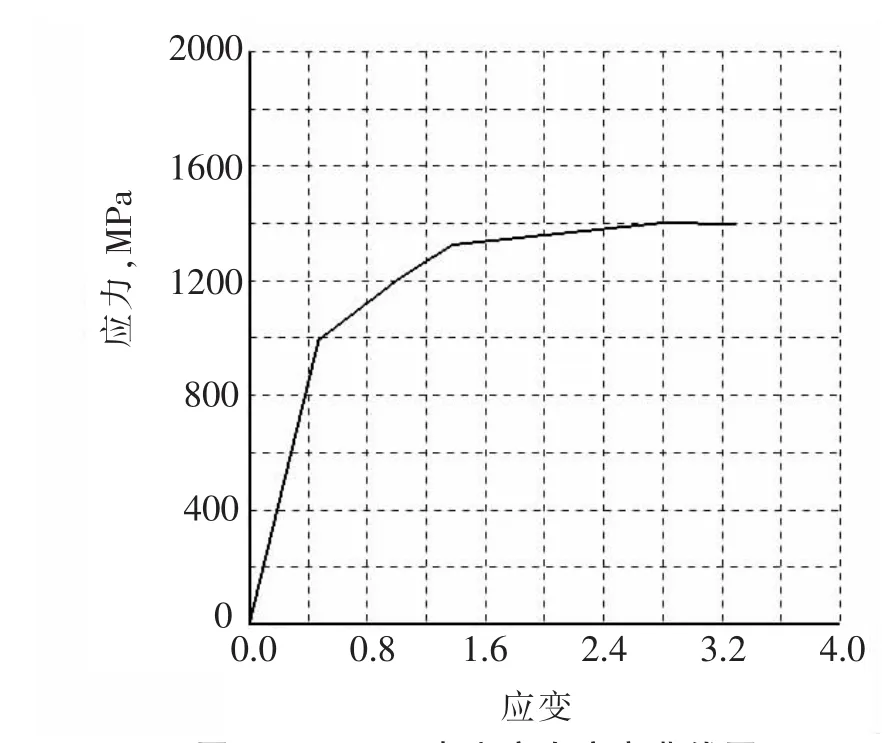
图3 20NiMn真实应力应变曲线图

为了方便分析各齿孔的应力分布情况，钻头各齿孔编号如图4所示。图5所示的是过盈量为0.01mm时输入真实应力和真实应变后得到的钻头本体的vonMises应力云图，从图5可以看出钻头本体上的应力主要集中分布在各齿孔周围，最大应力为1017MPa，出现在齿孔O8根部。喷嘴主要受流体的压力作用。而流体的压力很小，可以忽略不计，所以喷嘴周围的应力分布很小。除去齿孔周围的区域，钻头本体上大部分区域的应力值都比较小，远远低于屈服应力1010MPa，只有局部位置的应力接近或超过屈服应力，此时钻头本体主要处于弹性变形阶段，还有很大的强度盈余，可以进一步增大过盈量。

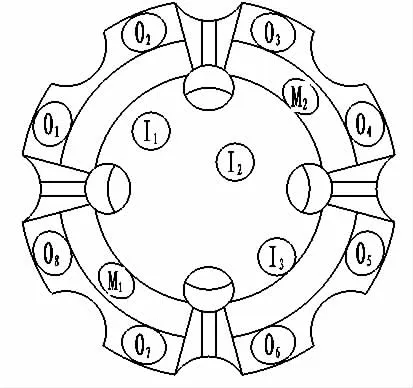
图4 齿孔示意图

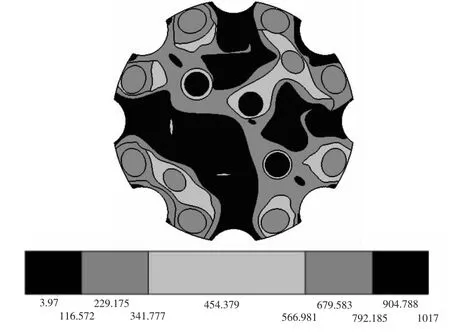
图5 0.01mm过盈量的vonMises应力云图

图6所示的是过盈量增大到0.02 mm后输入真实应力和真实应变后得到的钻头本体的vonMises应力云图。随着过盈量的增加，最大应力增大到了1216MPa，但应力分布情况是相似的。图6b清楚地显示出，由于孔M1、M2与孔O7、O8、O3、O4的间距比较小，在齿孔O7、O8和M1以及O3、O4和M2之间应力是比较高的，已经大于屈服应力，产生了塑性变形，但是塑性变形区域比较小，没有贯通齿孔之间的区域，从整个钻头本体看来，绝大部分区域的材料仍然处于弹性阶段，通过增大过盈量还可确保获得更高的固紧力。

图6 0.02mm过盈量的vonMises应力云图

图7所示的是过盈量增大到0.03mm后输入真实应力和真实应变后得到的钻头本体的vonMises应力云图。随着过盈量的增加，最大应力增大到1318MPa，齿孔周围的高应力区域进一步扩大。图7b清楚地显示出，齿孔O7、O8和M1以及O3、O4和M2之间高于屈服应力的区域进一步扩大。并且出现了塑性变形区连通的情况。相邻齿孔因过盈配合产生的装配应力场可能会出现塑性区迭加的情况，这对柱齿来说是非常重要的。如果出现塑性区迭加的情况，将会严重降低钻头柱齿的固紧效果。当柱齿受到的冲击载荷传到钻头本体时，由于钻头本体齿孔附近的材料已经处于塑性屈服状态，在冲击力的作用下将发生塑性流动，导致齿孔扩大变形，柱齿将从齿孔中脱落。

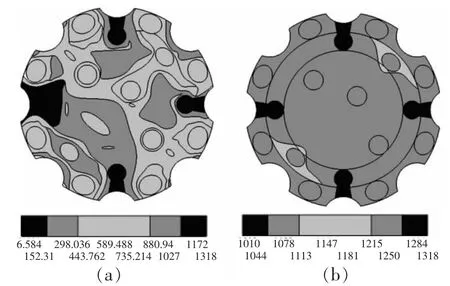
图7 0.03mm过盈量的vonMises应力云图

除去齿孔O3、O4、O7和O8，钻头本体上第一圈的其它齿孔，塑性变形区域主要分布在齿孔圆周的较小区域，而钻头中心部位的齿孔I2的塑性变形区域更小。齿孔I1和I3远离其它齿孔，应力分布受其它齿孔的影响较小，取齿孔I1沿孔深度的vonMises应力曲线如图8所示。由图8可以看出，在相同的过盈量下，应力沿齿孔深度方向的分布是变化的，最大应力为984MPa，位于孔深约9mm处的孔底倒角上端，低于屈服应力1010MPa，过了最大应力点后，在齿孔倒角处应力迅速降低。总之，齿孔I1和I3周围的材料仍然处于弹性状态，还有进一步增大过盈量的可能。

图9所示的是过盈量增大到0.05 mm后输入真实应力和真实应变后得到的钻头本体的vonMise应力云图。此时钻头本体上的最大应力为1415MPa，出现在齿孔O8的根部，已经接近了材料的强度极限1420MPa，这是不允许的。此时，不仅齿孔O7、08和M1以及O3、O4和M2之间高于屈服应力的区域进一步扩大，而且齿孔I2与M2之间的区域也出现了塑性区迭加的情况。

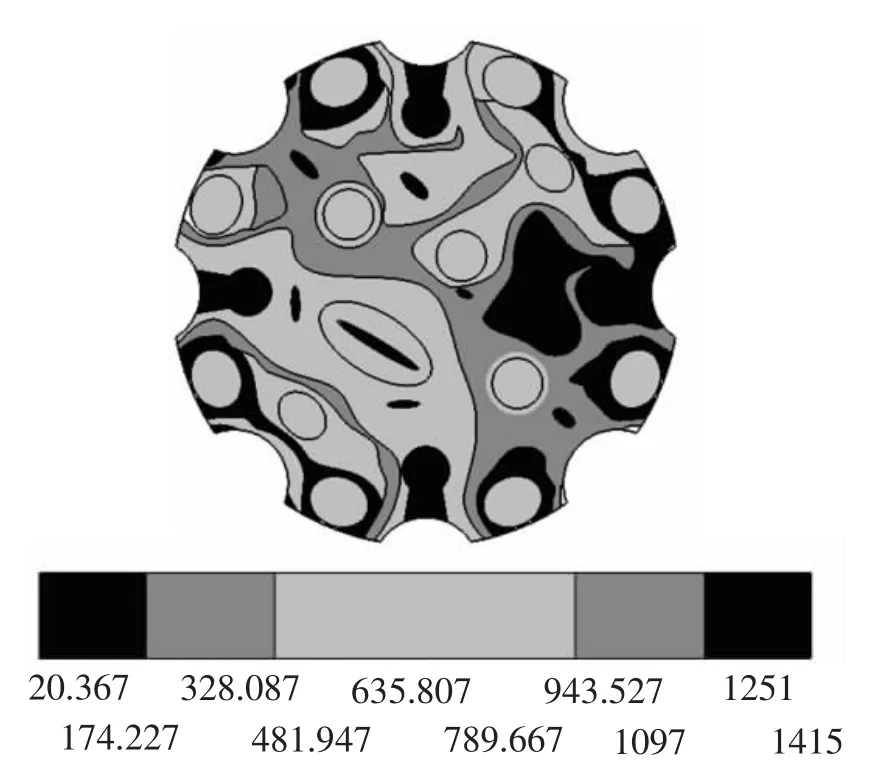
图9 0.05mm过盈量的vonMises应力云图

5 结语

通过以上分析，我们决定对Q13115-H64型潜孔钻头做出如下改进：

（1）通过改进布齿设计，增大齿孔O7、O8和M1以及O3、O4和M2之间的间距，消除齿孔周围的塑性区迭加，提高钎体对柱齿的固紧力。

（2）针对钻头本体不同的齿孔间距，采用不同的配合过盈量，解决在相同的过盈量下齿孔间间距不同产生的应力分布也不同的问题，以保证钻头上所有柱齿固紧效果都达到最优。

（3）调整柱齿加工工艺，将柱齿齿根磨成一定的锥度，这样可以使孔壁深度方向的应力场分布更加均匀，在提高固齿质量的同时也有利于制造钻头时的镶齿作业。

[1]单代伟等.潜孔钻头结构参数与井底流场关系研究[J].天然气工业,2007，27(2).

[2]练章华等.球齿过盈配合接触问题的计算机模拟研究[J].石油学报，2002，23(2).