剩余压紧力条件下滑靴副的油膜特性及功耗*
孙毅 姜继海 刘成强
(1.哈尔滨工业大学机电工程学院,黑龙江哈尔滨150080;2.浙江大学流体传动及控制国家重点实验室,浙江杭州310027)
当前针对轴向柱塞泵滑靴的设计最常采用的是静压支承和剩余压紧力方法.然而对于变量柱塞泵而言,由于转速、负载和斜盘倾角等工况条件的改变,无法保证滑靴总是保持在静压支承状态,因此,现阶段国内外在高压、大排量柱塞泵中对滑靴的设计普遍采用的是剩余压紧力方法.当滑靴在剩余压紧力状态下工作时,滑靴底面的油膜特性是影响滑靴副材料摩擦磨损的关键.
对于滑靴油膜的研究国内外均有报道,伯明翰大学的Hooke等[1-3]研究了柱塞泵/马达在低速情况下滑靴副压紧比及孔口尺寸对静压推力支承的承载能力的影响,并且搭建了能够检测柱塞泵滑靴副性能和油膜厚度以及高压泄漏损失的试验台.文献[4]中在考虑液压油的压粘效应、油膜表面的压力弹性特性及油膜的动态刚度的前提下研究了滑靴油膜的压力分布和负载特性,并在此基础上对高压柱塞泵的系统设计和参数辨识提出了创新性的依据.Tsuta等[5]建立了关于柱塞泵滑靴副的多体动力学模型和滑靴和斜盘相互作用时周边液压油的动态性能模型,列出了滑靴副的运动方程并且建立了液压油的模型,利用Newmark-beta方法求解出了这一系统的动力学特性.Tanaka[6]利用电涡流位移传感器测得了滑靴副静压支撑时的动作,推导出了考虑滑靴接触表面粗糙度的滑靴副静压支撑的数学模型,通过试验验证了模型的合理性.
文中通过Matlab编程对滑靴的油膜压力场进行数值求解,得到滑靴油膜的动态特性,在此基础上研究了滑靴副的功耗随负载和滑靴转速的变化规律.
1 滑靴副的结构及工作原理
目前最常采用的滑靴结构如图1所示.柱塞腔的高压油通过柱塞和滑靴中的阻尼小孔引入到滑靴底部的油池,使滑靴上产生液压反推力,油池的油液再通过滑靴的辅助支承带泄漏到柱塞泵的壳体腔内.理论上,合理的设计可以使柱塞对滑靴的压紧力与上述反推力相互平衡,产生静压支承效应,从而保持可靠的流体润滑,以减小滑靴和斜盘间的磨损.然而实际中,斜盘倾角、转速和负载的改变均会对滑靴的静压支承产生影响,所以滑靴的静压支承在现实中难以实现.

图1 滑靴的结构示意图Fig.1 Structure profile of slipper
当滑靴的反推力不足以平衡滑靴所受的压紧力时,滑靴就会在剩余压紧力状态下工作,此时靠滑靴和斜盘之间形成的边界油膜来减轻摩擦副的磨损.
2 滑靴副的运动和受力分析
由于滑靴的磨损主要发生在排油区,而静压支承和剩余压紧力设计方法也是针对滑靴排油区的情况而言,即考虑滑靴承受高压油作用的情形,所以文中主要研究滑靴在排油区时的受力情况.
图2所示为滑靴的运动轨迹.假设斜盘倾角为γ,柱塞分布圆半径为 R,取坐标系 O-x,y,z,则由此坐标系可以看出,滑靴沿垂直于缸体轴线方向的运动轨迹是个圆.而滑靴在斜盘平面O'y'z'上的运动轨迹是一椭圆,椭圆的长短轴的长度在文献[7]和[8]中均有描述.如果柱塞以角速度ω按图中所示的方向旋转,并且以下死点位置为起始位置,则当滑靴转到0°~180°时泵处于吸油区,滑靴转到180°~360°时泵处于排油区.
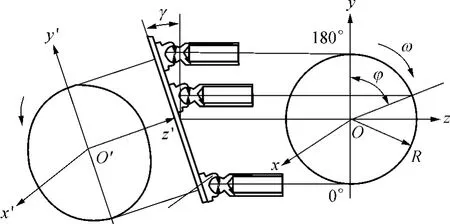
图2 滑靴的运动轨迹Fig.2 Motion trajectory of slipper
图3所示为滑靴的受力情况,柱塞泵工作过程中滑靴受到的力主要有:柱塞作用于滑靴的垂直于斜盘的分力fp,弹簧对单个滑靴的水平作用力ft,柱塞对滑靴的轴向惯性力fg和滑靴底面油池产生的分离力 F[7].

图3 滑靴的受力分析Fig.3 Force analysis of slipper
柱塞压力油作用到斜盘上的垂直分力fp可以表示为

式中,d是柱塞直径,ps是柱塞排油区的压强.
弹簧对滑靴的水平作用力可以由式(2)表示:

式中,fa是中心弹簧的预压缩力,Z是柱塞个数.
柱塞对滑靴的轴向惯性力fg可以表示为

式中,φ是图2中所示柱塞瞬时转过的角度,m是单个滑靴与相连柱塞的质量.
滑靴所受的总压紧力f可以由式(4)表示:

由式(3)和(4)可以看出,即使当柱塞与滑靴的结构尺寸、柱塞泵的转速和斜盘倾角确定时,柱塞与滑靴的惯性力造成的影响也随滑靴转过角度的不同而发生变化,所以与之对应的滑靴所受的总压紧力是随滑靴转角不断变化的,造成滑靴底面油池的压力也随之不停地变化,最终使滑靴油膜的厚度不断变化.所以通过计算单个滑靴在排油区的压紧力就可以得到其在排油区的油膜模型.
要想对滑靴产生足够的反推力以平衡大部分来自柱塞的压紧力,滑靴底面至少要有一个容腔,容腔内的压力通过容腔四周缝隙流动,产生一定的压力分布,容腔和节流边内压强产生的力即分离力,其支承情况如图4所示.图中F为滑靴底面油腔压强产生的分离力,pr为滑靴底面油腔的压强,h为底面的油膜厚度,R1和R2分别是滑靴底面半径和滑靴油池的半径.
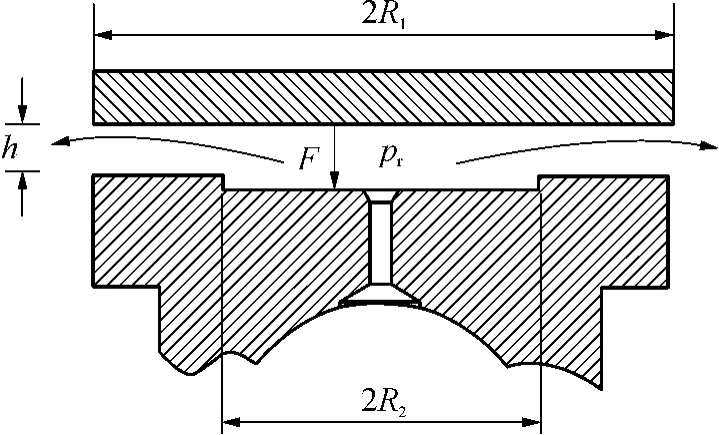
图4 滑靴的底面支承力Fig.4 Supporting force of slipper bottom
滑靴结构的压力-流量(Q)特性[8]可以由式(5)表示:

式中,d1是阻尼管直径,l是阻尼管长度,μ是油液的动力黏度.
可变阻尼的压力-流量特性相当于平行圆盘缝隙流动的情况,即

由流量连续方程[8]可知式(5)和(6)所示流量相等,即
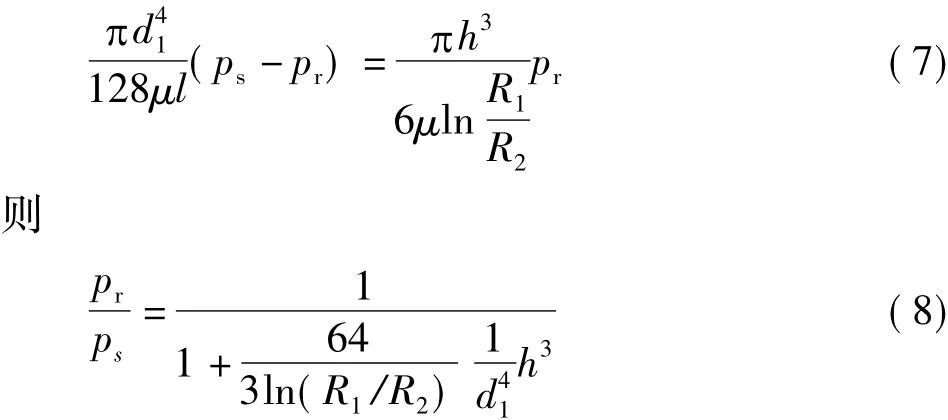
由式(8)可以看出,当滑靴的结构一定时,pr可以表示为ps的关于h的函数.
剩余压紧力状态下滑靴底部油膜产生的分离力F可以表示为

此时的剩余压紧力fsy则可以表示为

式(10)中的pr可以由式(8)中的ps确定,因此只要柱塞泵的结构尺寸和系统负载确定,则当滑靴在排油区转过不同角度时,其所受的剩余压紧力都可以表示成为h3的函数.
当滑靴在剩余压紧力状态下工作时,滑靴底面油池的油压只能承受由柱塞传及的一部分压紧力,剩下一部分压紧力将滑靴支承面压紧于斜盘平面上,使之在极薄的油膜下滑行,高速剪切油膜,滑靴支承面下的油液由于压差和高速剪切的缘故,其温度增高而发生膨胀,以至产生压力流动,这时在斜盘与滑靴底面形成的间隙间将产生一种被称为热楔力支承的支承力,此时由热楔支承力来承担剩余的那部分压紧力,根据文献[8],热楔支承力可表示为

式中,α0是油液的容积膨胀系数,ρ为油液的密度,ce是油液的比热容,g是重力加速度,G为热功当量,r为椭圆上任一转角对应的矢径.
由式(11)可以看出,当滑靴的结构和液压油的属性确定时,热楔支承力是关于1/h4的函数.
热楔支承力和剩余压紧力的关系可以用式(12)表示:

根据式(10)的推导可知,剩余压紧力fsy为h3的函数,而由式(11)的推导可知热楔支承力N为1/h4的函数,因此式(12)中当剩余压紧力与热楔支承力相等时,可以得到关于油膜厚度h的7次微分方程.求解后得出只有一个满足条件的正实数根,是滑靴在转过该角度瞬间所对应的底面的油膜厚度.
3 剩余压紧力状态下滑靴副的油膜特性
3.1 滑靴油膜厚度的变化
当滑靴处于排油区时,滑靴承受着巨大的压紧力,此时滑靴底面油池压力场和油膜厚度如果形成得不好就会造成滑靴底面支承力不够,甚至造成滑靴与斜盘之间的干摩擦;另外,滑靴与斜盘缝隙间的泄漏也会对柱塞泵的容积效率和机械效率造成直接影响.因此,滑靴底面油池的压力和油膜厚度是衡量滑靴副油膜形成好坏的重要指标.
既然图2中已经假设当滑靴转到0°~180°时泵处于吸油区,则滑靴转到180°~360°时泵处于排油区,因此,只需分析滑靴180°~360°区间的情况.图5所示为滑靴在剩余压紧力状态下油膜厚度随转角的变化曲线,该曲线利用剩余压紧力和热楔支承力相平衡,通过对滑靴副油膜厚度高次方程的求解得到,仿真参数如表1所示,负载压力分别为30 MPa和4MPa,柱塞泵的转速为1500r/min.
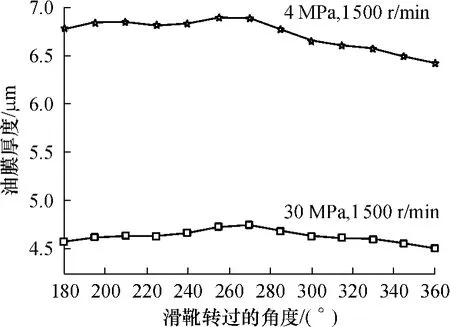
图5 剩余压紧力状态下滑靴油膜厚度随转角的变化Fig.5 Variation of film thickness of slipper with rotation angle under redundant pressing force condition
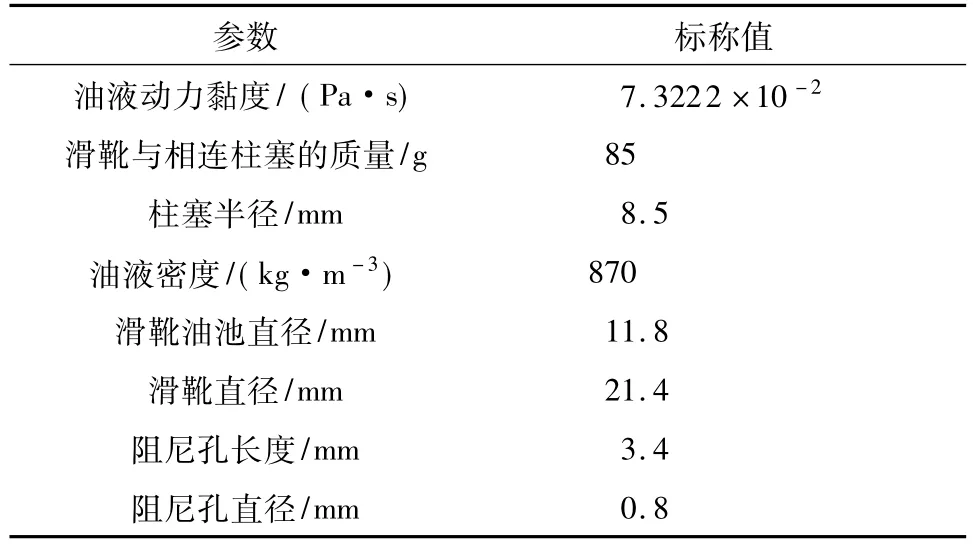
表1 滑靴副的主要参数Table 1 Main parameters of slipper pair
从图5中可以看出,滑靴的油膜厚度随转角而变化,并且负载压力越大对应的滑靴油膜厚度越小,在滑靴转到270°时油膜厚度最大.这是因为滑靴所受的总压紧力f是随着转角变化的,并且从式(3)和(4)可以看出,在负载不变的情况下,当滑靴转到270°时所受到的总压紧力最小,与之对应的剩余压紧力也最小,所以热楔支承力所承担的力也最小,根据式(11),当滑靴的结构、转速和油液属性不变时,只有油膜厚度变大时滑靴的热楔支承力才能相应减小.
由于柱塞泵内部结构紧凑,滑靴底面的流体流动状况复杂,所以在其内部安装测量装置一直是比较困难的,特别是对于高速转动的滑靴而言,几乎不可能在结构紧凑且又不断运动的滑靴上测出滑靴底面流动参数的连续变化.由于实验条件所限,文中借用燕山大学潘永阁教授的实验数据[9]证明结论的正确性.文献[9]中测试了剩余压紧力条件下当系统压力为4MPa、转速为1500r/min时柱塞泵滑靴的油膜厚度,并且得出“压油区滑靴的油膜厚度平均值约为8μm,并且不会形成规律性的稳定油膜”的结论,这与图5中相同工况条件下滑靴油膜厚度的仿真结果一致,充分说明了文中提出的滑靴在剩余压紧力状态下运行时的数学模型是正确的.
3.2 负载和转速对滑靴油膜厚度的影响
分析式(10)和(11)可知,负载和滑靴转速均会对滑靴底面的油膜厚度产生影响,图6(a)和6(b)分别为在剩余压紧力状态下,当负载和滑靴转速(不考虑滑靴自转)发生变化时,滑靴底面的油膜厚度的变化曲线.

图6 剩余压紧力状态下负载和转速变化时的滑靴油膜厚度随转角的变化Fig.6 Variation of film thickness of slipper with rotation angle when load and rotating speed change under redundant pressing force
由图6可以看出,剩余压紧力状态下,当滑靴的转速一定时,负载与滑靴底面油膜厚度呈负相关;当工作的负载一定时,滑靴转速与油膜厚度呈正相关.当滑靴的转速不变时,负载越大对应的剩余压紧力也越大,于是平衡剩余压紧力所需的热楔支承力也越大,根据式(11),当滑靴的转速不变时,只有油膜厚度变小,热楔支承力才会变大,才能平衡掉负载变大带来的影响.因此当滑靴的转速一定时,负载与滑靴底面油膜厚度呈负相关;当滑靴处于静止状态而不运动时,在剩余压紧力的作用下滑靴油膜厚度近似为零,只有滑靴高速运转时,底面的油液才会由于压差和高速剪切导致温度增高而发生膨胀,产生压力流动,此时热楔支承力才会起到辅助支承的作用以平衡剩余的压紧力,当负载不变时,剩余压紧力的变化仅由柱塞的惯性力造成,因此其变化量很小,而滑靴转速ω的大幅提高会造成式(11)中分子项的大幅提高,导致热楔支承力急剧增加,为了维持热楔支承力与剩余压紧力的平衡,式(11)中的分母项需要相应提高,即油膜厚度增加.因此当工作的负载一定时,滑靴转速与油膜厚度呈正相关.
4 滑靴副功耗的计算及分析
4.1 滑靴引起的功耗损失及影响
当滑靴在斜盘上高速运行时,滑靴与斜盘的缝隙间存在油液的流动,其中既有压差流,又有剪切流.在压差流作用下,滑靴与斜盘缝隙间油液的功耗损失W1可以用式(13)表示:

式中:Δp为压强差.
剪切流主要由滑靴与斜盘间的相对运动形成,当滑靴副不出现干摩擦时,如果忽略滑靴的自转,假设滑靴只作公转运动,则此时缝隙中由油液摩擦引起的功耗损失W2可由Newton内摩擦定律计算,此时油液摩擦造成的功耗损失可以表示为

式中:v是滑靴滑动的线速度.
无论是剪切流造成的功耗损失还是压差流造成的功耗损失,二者最终都将转换成油液的内能,引起油液温度升高,黏度下降,严重时会引起滑靴底面油腔压力的降低和支承油膜厚度的显著减小,导致油膜形成的条件更加恶劣,甚至引起液压元件受热膨胀,使不同材料的运动副之间间隙发生变化,造成动作不灵或“卡死”.因此滑靴副的压差流和剪切流的功耗损失是衡量油液温度的重要指标.
4.2 负载和转速变化对滑靴功耗损失的影响
由于负载的变化会直接影响滑靴底面油腔的压力和底面的油膜厚度,并间接影响到滑靴泄漏量,最终反映到油液内能的增加,因此有必要对负载变化时滑靴的功耗损失进行分析.图7(a)所示为当转速为1500r/min时,不同负载对应的滑靴的功耗损失情况.图7(b)所示为负载为30MPa时,不同转速时对应的滑靴功耗状况,仿真参数仍然如表1所示.

图7 剩余压紧力状态下负载和转速变化时的功耗损失随转角的变化曲线Fig.7 Variation of power consumption of slipper with rotation angle when load and rotating speed change under redundant pressing force
由图7可以看出,负载变化对滑靴功耗损失的影响远小于转速变化对功耗损失的影响.这是因为当滑靴转速不变而负载变大时,滑靴底面油腔与外界的压差虽然增大,但滑靴底部的油膜厚度也变薄,由式(6)可以看出滑靴内油液的压差泄漏量与h3成正比,而根据式(14)可知剪切流的功耗与油膜厚度h成反比,所以,因负载变大造成的油膜变薄在增加了剪切流的功耗损失的同时,还减小了泄漏量,因此在某种程度上抑制了压差流的功耗损失.另外,式(14)中剪切流的功耗损失虽然与油膜厚度h成反比,但却与v2成正比,而线速度v与角速度ω正相关,因此滑靴的转速的变化对剪切流的影响要大于油膜厚度h的影响.当滑靴的转速提高而负载不变时,油膜厚度变大带来的剪切功耗的减小不足以补偿由于速度平方的提高带来的剪切功耗的增加,相反油膜厚度变大还造成了压差泄漏量的增大,所以转速变大不仅造成了剪切流功耗损失的增大而且大大增大了压差流的功耗损失.
5 结论
(1)文中提出了一种研究剩余压紧力状态下滑靴副油膜动态特性的新方法,在将滑靴副油膜的热楔支承力效应引入油膜模型的基础上,首次以求解油膜厚度7次方程的形式,精确获得滑靴在剩余压紧力状态下运行时的油膜厚度.
(2)剩余压紧力状态下,负载的变大会使滑靴底面油膜变薄,并且增大剪切流的功耗损失,但油膜变薄对压差流的功耗损失有一定的抑制作用;而滑靴转速的提高有利于热楔支承力的形成,并有助于提高油膜厚度以减少磨损,但速度的提高不仅会增大剪切流的损失而且会增大压差流的损失,因此转速对滑靴功耗的影响远远大于负载变化的影响.
(3)滑靴旋转速度的提高有助于滑靴油膜厚度的提高,而负载的增大导致油膜变薄,因此从滑靴使用寿命的角度考虑,高压低转速工况是不利的,但高转速下滑靴功耗带来的油液内能的增加同样不容忽视.
[1] Koc E,Hooke C J,Li K Y.Slipper balance in axial pistonpumps and motors [J].ASME J Tribol,1992,114(4):766-772.
[2] Hooke C J.The lubrication of slippers in axial piston pumps and motors:the effect of tilting couples[J].Proc Inst Mech Eng,Part C:J Mech Eng Sci,1989,203(C):343-350.
[3] Li K Y,Hooke C J.Note on the lubrication of composite slippers in water-based axial piston pumps and motors[J].Wear,1991,147(2):413-437.
[4] Pang Z,Zhai W,Shun J.The study of hydrostatic lubrication of the slipper in a high-pressure plunger pump[J].STLE Tribol Trans,1993,36(2):316-320.
[5] Tsuta T,Iwamoto T.Combined dynamic response analysis of a piston-slipper system and lubricants in hydraulic piston pump [J].ASME,1999,396:187-194.
[6] Tanaka Kazuhiko.Motion characteristics of slipper bearing in swash plate type piston pump and motor[J].Transactions of the Japan Society of Mechanical Engineers Part,2007,73(728):1236-1244.
[7] 闻德生.斜盘型开路式轴向柱塞泵[M].北京:机械工业出版社,1993:53-60.
[8] 闻德生.液压元件的创新与发展[M].北京:航空工业出版社,2009:96-128.
[9] 潘永阁,韩德才,周铁农.轴向柱塞泵几种滑靴的实验研究 [J].燕山大学学报,1990,6(1):9-14.Pan Yong-ge,Han De-cai,Zhou Tie-nong.Experimental study on dynamical characteristics of slippers in axial piston pump [J].Journal of Yanshan University,1990,6(1):9-14.

