为创造“数学物质”探路[1]①

许槑

(中国科学院 北京 100190)

已知物质除常见的固、液、气三态外，还有被称为第四态的等离子体以及近年来发现的玻色-爱因斯坦凝聚态物体.也许，在不久的将来人们会见到被称为“数学物质(Mathematical matter)”①的新客体.

数环依次扣接并形成圈状如图1所示.1892年，德国从事于纽结理论(Knot theory)的数学家布鲁恩(H.Brunn)研究了该几何图形的拓扑性质，因而被命名为Brunnian rings(以下简称Brunn环结).三环顺次扣接是其特例被称为Borromean rings(以下简称Borrom环结).剪开任何一环，整个环圈便不复存在了.

1970年，现在在华盛顿大学工作的前苏联理论物理学家埃菲莫夫(V.Efimov)曾预言Borrom环结的拓扑可能会反映在自然界尚未发现的三个粒子的结合中[2].果然，2006年，研究人员在过冷的铯原子气体中发现了这一所谓的“Efimov状态”，每个铯原子都由单键与另两个联系，挟起一个铯原子，另两个也跟着动起来.2010年，日本的一位研究人员发现原子核之间键的Borrom环结.挪威理工大学的数学家巴斯(N.Baas)认为，“人们可将这样的结构做为配方，构建新的物质.”

巴斯既研究了具有4个和更多环的Brunn环结，还以Brunn环结为单元，将它们按同样的方式扣接形成所谓的“超级结构(hyperstructures)”.但这种超级结构就其拓扑性质而言已根本上不同于自然界中人们已见到的任何物质，如果大群粒子能被构建成按上述方式键结，则由它们配制成的物质将具有以前从未见到的特性.巴斯和纽约大学的西曼(N.Seeman)一道考虑如何构建超级结构.西曼说：“看来，数学真的是很好的预言家，我的每一个猜想，用数学方法都能实现.”他曾在1997年用DNA链合成Borrom环结.

巴斯还考虑利用量子过程超长距离魔鬼般的作用——纠缠态[3]来获得：如果诸粒子开始时以复杂的Brunnian方式环结在一起，即使它们隔开时，也能彼此互相影响.

巴斯说，一旦这些环结被拓扑学指认，我们就能回过头来在描述量子理论之数学的薛定谔方程中寻找它们.从那儿，一准可能在实验室中创造新的量子态,从而能够提供建造超强功能的量子计算机的新途径;这种计算机可用于处理诸粒子的量子态所携带的能同时存在于许多状态的量子信息.这样的计算机一定能够同时进行巨量的运算.

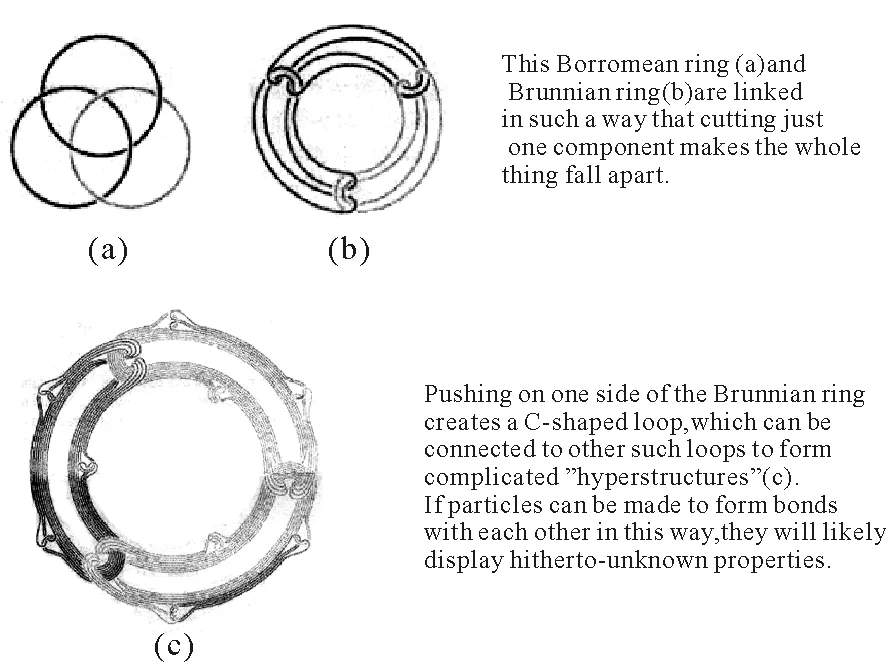
图1 Brunn环结及其放大的形态

1 Michael Brooks.Make way for mathematical matter.New Scientist (05 Jan.2011)

2 V.Efimov,Energy levels arising from resonant two-body forces in a three-body system.Physics Letters B,vol.33,issue8(21 Dec.1970).563～564

3 许槑.纠缠态——物理学中最奇异的现象.物理通报，2004(9):1～3