巧解竞赛题的一种方法——“补偿法”

肖建华

(太仓高级中学 江苏 太仓 215400)

在物理学的学习过程中，当常规方法对复杂的物理问题无能为力时，一些特殊的方法往往能发挥其独特的威力，将复杂的物理问题由难变易，由繁变简;补偿法就是一种有效可行的方法.所谓补偿法就是在与原问题和物理规律不相违背的前提下，适当补充一些物理条件，从而求解物理问题的方法.本文结合具体题例，简要总结了使用补偿法求解物理竞赛中万有引力、质心、感应电动势等基本物理量的问题，以及复杂的运动问题.

1 在力学中的应用

在力学中常常会遇到这一类问题:一个几何对称的物体中间被挖掉一部分.

1.1 用补偿法求万有引力

图1

解析：万有引力公式适用于真空中的质点，均匀球体可以等效成质量集中于球心的质点.本问题是求不规则的物体和质点之间的万有引力，没有现成的公式可以用，需要变换思维角度.假设把用同样密度的均匀分布的物质填满空穴，这样就形成了完整的均匀球体.完整的球体跟质点m之间的引力为

F=F1+F2

其中F1表示剩余部分对m的吸引力，所以

F1=F-F2=

1.2 用补偿法求质心

图2

解析：由于圆盘不是几何对称，一般都采取积分法求质心,但计算相当繁复.如果用补偿法处理，那就是在挖去的部分先填上密度和薄圆盘相同的物质Δm.补上Δm后，完整的大圆盘的质量为

M0=πR2ρ

大圆盘的质心坐标为

x0=0y0=0

根据质心坐标系，便可得到被挖去圆孔的薄圆盘的质心坐标为

评注：由此可见，对于此类几何均匀分布的有孔物体，巧用“补偿法”进行恰当的分割填补,再进行计算，比较简便.

2 在电磁场中的应用

2.1 用补偿法解决电场中的问题

【例3】一个绝缘的刚性细圆环，半径为R，质量为M，可以绕垂直于纸面的轴O自由旋转，但不能平动.此环长度均匀带电，电荷量为Q.在A点剪下一个小缺口，其空隙长度为l.开始时圆环静止不动，接通一个匀强电场E，让E既垂直于轴O，又垂直于半径OA，如图3所示，求圆环旋转的最大角速度.

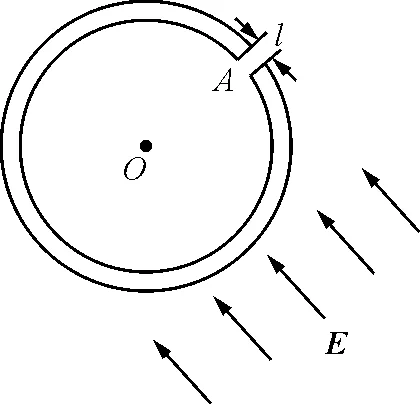
图3

根据动能定理

解得

评注：通过恰当的分割填补，可以使原来不在公式适用范围之内的问题变为可以直接应用公式解决的问题.

2.2 用补偿法解决磁场中的问题

【例4】一无限长圆柱，偏轴平行地挖出一个圆柱空间，两圆柱轴间距离OO′=d，图4为垂直于轴的截面.设大圆柱间存在匀强磁场，磁感应强度随时间t线性增大，即B=-kt.挖出的圆柱空间磁感应强度为零.现在空腔里放一长为L,与OO′在同一平面内且成60°角的金属杆AO′C.求杆中的感生电动势.

图4

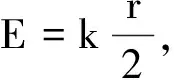
图5

评注：应用补偿法，在空腔内填补大小相同、变化率相同但方向相反的均匀磁场，使空腔内任意一点的感生电场可以看成是两个无限长的圆柱体产生的电场的叠加，使问题由繁变简，得到有效的解决.

2.3 用补偿法解决复合场中的问题

【例5】如图6(a)所示，A1和A2是两块面积很大、相互平行又相距较近的带电金属板，相距为d，

图6

两板间电势差为U.同时在两板间还有方向与均匀电场正交而垂直纸面向外的匀强磁场.一电子在左侧带负电的板A1上的小孔无初速释放.为使该电子不碰到右侧带正电的板A2.问所加磁场的磁感应强度至少要多大？(设电子所受的重力不计)

解析：电子在电磁场的复合场中做复杂的曲线运动，可以用数理方法解决，相对较为繁琐.可用补偿法处理，把复杂运动巧妙分解.

根据题意，电子进入板间初速度为零，设想此时电子具有沿图6(b)所示的y方向的速度+v和-v，使+v引起的磁场力恰好与电子在极板间受到的电场力相平衡，即v的大小满足

即

由此可见，+v引起的磁场力和电场力平衡使电子沿y轴方向做匀速直线运动，-v引起的磁场力使电子以-v做匀速圆周运动，于是，电子的运动结合起来，可视为是一个速度为v的向上的匀速直线运动和速率为v的匀速圆周运动的合成.

对匀速圆周运动，有

而要求电子不碰到A2板，则必须有

由上可得

评注：运用补偿法，引入大小相同方向相反的速度，将粒子的复杂运动分解成同一平面内的匀速圆周运动与匀速直线运动的合成，巧妙地运用了运动的合成和分解知识来处理复杂运动的过程，使问题简化.