例说微积分在大学物理中的应用

于希梅 毛安君

(淮阴工学院数理学院 江苏 淮安 223003)

微积分的应用，是近代科学得以起步发展的必要条件，也是大学物理区别于高中物理的一个基本特点．在大学物理教学中，合理明了地引入微积分，说明它对物理学的意义，以及点拨在应用微积分解决问题时的疑难，对于学生学好物理学以至各门自然学科都有重要意义．本文就此作些探讨．

1 曹冲称象与物理学中的微积分

曹冲称象的故事：曹操想知道象的重量(即质量).但当时没有那么大量程的称重仪器.众人各抒己见.一大臣讲将大象杀死，切割成小块称重.曹冲则以水的浮力为纽带，将象的重量转化为一块块石头的重量．从数学方法上讲，大臣与曹冲的逻辑思路无本质差别，但后者更巧妙且人性化．对曹冲来讲，称量象的重量是一个困难的问题，不妨称作“一般问题”；处理的方式是，通过分割将其转化成称量一块块石头的重量，然后将其相加；称量石头的重量很简单，可称作“基本问题”．就是说，曹冲将“一般问题”的答案转化成了“基本问题”的答案的叠加，而这也正是微积分解决问题的思路．以静电学中求一般带电体的场强为例进行比较说明．

【例1】如图1，求带电线段AB在P点产生的电场强度．

求带电线段在P点产生的场强是个复杂的“一般问题”，没有普遍直接的规律解答，因此将带电线段分解成电荷元．电荷元相当于没有大小和形状的点电荷，产生场强时具有简洁普遍的规律，求点电荷的场强即“基本问题”．整个带电线段的场强等于各电荷元的场强之和．虽然微积分方法分割时到了微元的程度，得到了最终的“基本问题”，从而更具有普适性；但处理问题的思路同曹冲称象一样，也是将“一般问题”的答案转化成了“基本问题”的答案的叠加．进一步讲，公理化科学体系的建立都是类似的思路，所有问题都分解成“基本问题”，公理就是“基本问题”的答案．可见曹冲称象的做法体现的不仅是微积分的思路，更是科学体系中的一种基本思想．

图1

在整个过程中有两个关键问题．(1)是否满足叠加原理．若两块石头各自称出的重量之和，不等于它们共同称量时的重量，则此方法失效．叠加原理在自然界中并不总是满足，一个简单的反例是水和酒精的体积混合．在考察一种物理现象时，探讨其是否满足叠加原理是个基本问题，在牛顿力学、电磁学、量子力学中都有体现[1]．(2)基本问题的答案．各基本定律给出的往往就是基本问题的答案，如牛顿定律、万有引力定律、库仑定律、毕奥-萨伐尔定律等．

求场强的问题.传统的讲法往往先给出点电荷的场强公式，再引入叠加原理，进而得到点电荷系和任意带电体的场强公式；而以曹冲称象的故事为引导来讲解，趣味性强.后者在分析解决问题的过程中引用微积分的思想及涉及到的关键点，思路明了，要点明确，逻辑性强，能够帮助学生举一反三，理解微积分在整个物理学中的重要价值．

2 涉及矢量的微积分运算

微积分和矢量代数是大学物理的基本数学工具．矢量一般需要投影到坐标轴上进行积分运算．

2.1 矢量积分运算的基本方法

矢量积分形如

矢量积分运算一般是把矢量写成坐标轴投影的形式，即

A=Axi+Ayj+Akk

微分变量dl、上下限和积分式中的各矢量，都用相应的投影形式表示，从而把矢量积分化为标量积分.因投影值Ai(i=1,2,3，代表三个坐标方向，下同)等于矢量大小A乘以其对相应坐标轴的方向余弦cosαi，因此Ai与坐标轴方向有关.若某坐标轴反向，则新夹角αi′=αi-π或αi′=αi+π，新方向余弦cosαi′=-cosαi，新投影值总是原投影值的负值．

【例2】如图2，以大小不变的力F拉大小不计的物体从A点到O点，求F所做的功．

图2

(1)以O点为原点，x轴正向如图2所示，则应用做功的公式

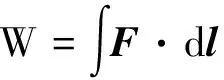
(1)

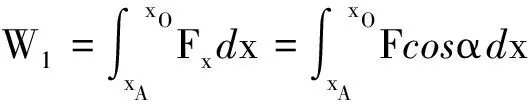
(2)

(2) 坐标轴反向为x′轴，原点仍为O点，则

(3)

因为功总大于零，即W>0，则(3)式中，-dx′>0,即dx′<0.

对比(3)式与(2)式，因坐标轴反向，各投影值均为原投影的负值，所以(2)式和(3)式积分相同.

2.2 矢量投影的一般方法

很多情况下，矢量起点不在坐标原点，不能直接向坐标轴投影，一般教材中往往根据几何关系给出其方向余弦，逻辑不甚严密．此时应根据矢量平移不变性，平移坐标轴使原点与矢量起点重合，进而得到其方向余弦．

仍以例1中的问题为例，根据点电荷场强公式可得电荷元在P点产生的场强dE．由于dE方向与r相同，可利用r的方向余弦进一步求dE在坐标轴上的投影值．因r起点不在坐标原点，可将坐标轴平移，使二者重合，如图3所示．则

(4)

(5)

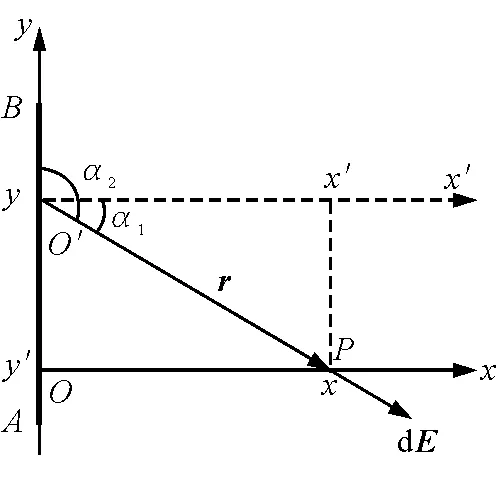
图3

对于(5)式，由于坐标轴的平移，因此有y′=-y或y=-y′．(4)式中推理与此类似．

3 结语

微积分是学习大学物理的基本工具，本文借助曹冲称象的故事阐述了微积分的物理意义，以加深学生的理解，并说明了矢量微积分计算中的两点细节问题，帮助学生进行正确运算．

参考文献

1 费恩曼，莱顿，桑兹,等，著.潘笃武，李洪芳译．费恩曼物理学讲义(第2卷)．上海: 上海科学技术出版社，2005．42，171