利用磁矢势求解涡旋电场*

丁红伟 任常愚 李海宝

(黑龙江科技学院数力系 黑龙江 哈尔滨 150027)

1 引言

一般大学物理教材[1～3]对涡旋电场的计算问题所谈甚少，只局限于截面是圆形的轴向时变磁场．这一方面给不少学生带来错误的假象，认为只有截面是圆形的轴向时变磁场周围的涡旋电场的表达式才是显性的，而其他时变磁场周围的涡旋电场的表达式则是隐性的，不能直接给出；这是教材拓展不够所造成的错误理解.

在麦克斯韦方程组的变形公式

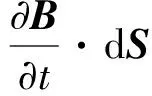
式中EC为涡旋电场的电场强度，B为时变磁场的磁感应强度.对于截面是圆形的轴向时变磁场周围的涡旋电场，电场强度与磁感应强度的关系可表示为

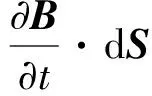
(1)

此结果只对于上述特殊情况才是对的.可学生的定式认为(1)式可以应用于任何时变磁场所激发的涡旋电场，造成求解的错误，有时根本不能求解．为此，本文假设读者已掌握了一些基本的矢量知识为前提来探讨磁矢势和涡旋电场的关系，进一步求解涡旋电场，以期深化学生对磁矢势和涡旋电场概念的理解．

2 理论依据

一般在似稳场的情况，即场量变化足够缓慢时，场源与场量之间的条件关系与稳定场相似．在静磁场条件下有[4～5]

(2)

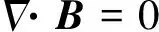
(3)

即静磁场是有旋无散场．根据矢量知识，对于矢量f，有

可以将B定义为另一个矢量的旋度．即

(4)

其中，矢量A就称为磁场的矢势．由矢势A可完全确定磁场B．但是，由此场B却不能唯一的确定矢势A．为此，需要加上一点限制

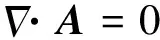
(5)

称这个限制条件为库仑规范．

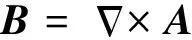
(6)

而在柱坐标系中的形式为

(7)

在由均匀线性介质构成的无界空间中，把(2)、(4)式和B=μH结合起来得到和静电场中的静电势φ(x)的泊松方程

形式类似的方程

所以此两个方程的解的构造上相同.由

可直接获得磁矢势

在线电流的情况下，上式通过jdV′～Idl′替换，变成

(8)

此式在实际求解磁矢势A中常用．

麦克斯韦的感生电场假说指出，变化的磁场在其周围空间激发感生电场与空间有无导体、导体回路无关．这种感生电场为涡旋电场EC，其主要性质可概括为[6]

(9)

上式通过积分变换可得

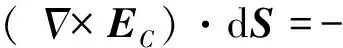
进一步知

把(4)式代入得

(10)

3 应用磁矢势求解涡旋电场举例

如何求解载有变化电流的长直导线周围的涡旋电场[7]？这是学生经常会提出的问题，很显然用现行教材中给出的方法不能胜任．这时考虑一下我们上面的理论分析，只要能求出长直导线周围的磁矢势A就可求出其周围涡旋电场分布，而求磁矢势A的方法在上面已经明确．

由于其周围磁场分布的特点我们采用柱坐标系可揭示

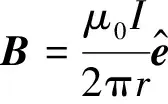
根据(8)式知

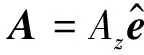
由柱坐标的分量表示式(7)可建立方程

得

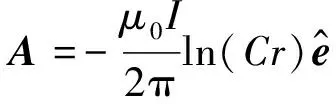
式中C为待定常量.由(10)式即可求得

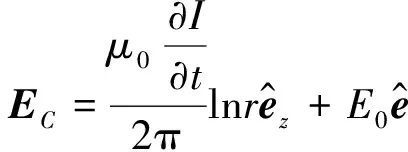
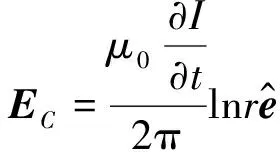
涡旋电场分布图像如图1所示．

图1 载流直导线周围的涡旋电场分布

我们再看，载有变化电流的圆环周围涡旋电场的分布情况．结合特点，选择球坐标系，可以很容易得到磁矢势A(x).由旋转对称性可知A与ψ无关．如图2，选xOz平面上的一点p,在该点上有

其中

dly′=dl′cosψ=acosψdψ

在限定条件2Rasinθ≪(a2+R2)下，可以把r级数展开，取至第二项得

最后根据(10)式可求得EC．

图2 载流圆环

4 结论

由以上的理论分析和实际的例子，我们不难发现，一般传统教材对于涡旋电场问题的求解仅就特殊情况作了处理.而我们利用磁矢势A求解涡旋电场过程的简洁性、适用性的探讨，足以澄清了学生的疑问，即只有截面是圆形的轴向时变磁场周围的涡旋电场的表达式才是显性的，而其他时变磁场周围的涡旋电场的表达式则是隐性的，不能直接给出的盲点．但也应该注意到它的应用范围应该是似稳场的条件下．建议教材编写者在此方面做适当的拓展．

参考文献

1 李晓萍，任常愚，尹向宝.大学物理学．北京：机械工业出版社，2009

2 唐炳华，赵世杰．大学物理学.北京：学苑出版社，1994.172～199

3 程守洙，江之水.普通物理学.北京：高等教育出版社，1982.218

4 赵凯华,陈熙谋.电磁学.北京:高等教育出版社,1985.486～488

5 费曼.费曼物理学讲义.上海:上海科学技术出版社,1981.167～174

6 郭硕鸿.电动力学.北京:人民教育出版社，1979

7 苏景顺.关于长直导线通以变化电流产生的涡旋电场.大学物理，1995，14(1)：45～47