4×n阶网络的等效电阻理论及实验研究

吴惠 潘桂源 刘应开

(云南师范大学物理与电子信息学院 云南 昆明 650092) (昭通师专物理系 云南 昭通 657000)

研究网络等效电阻有一定的实际意义,许多实际问题都可以通过构建电阻网络模型进行模拟和计算研究.文献[1]研究了3×n阶电阻网络的等效电阻,文献[2]研究了2×n阶电阻网络的等效电阻.本文利用文献[1]和[2]的矩阵变换方法研究4×n阶电阻网络的等效电阻，并用NI Multisim 10 模拟软件对4×n阶电阻网络进行模拟实验测量，从而验证计算结果的准确性．

1 电阻网络的结构特点

如图1所示的电阻网络,网络元中的横向、纵向电阻均为r.网络的a行与e行关于c行、b行与d行关于c行具有完美的对称性.利用文献[2]的电流分析法,若电流从a输入至e输出,则c行中的电阻必无电流流过,当仅求a、e两点间的等效电阻Rae的规律时,可以将c行的电阻拆去,这样4×n阶梯形电阻网络便退化为3×n阶梯形网络,如图2所示.

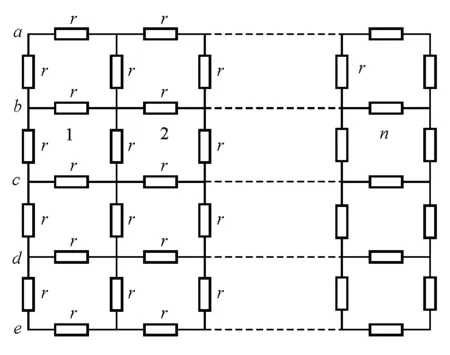
图1 4×n阶电阻网络图

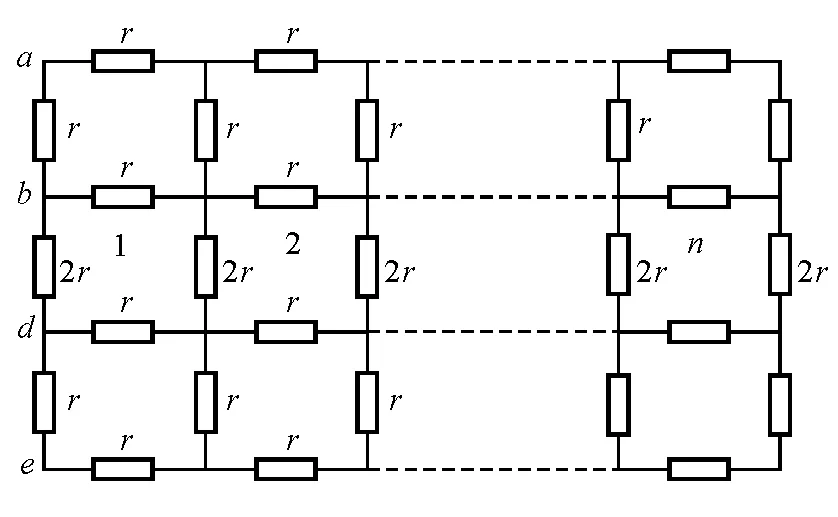
图2 4×n阶梯形电阻网络等效电路图

2 电阻网络的电流规律

根据文献[1]中的电阻网络中的电流规律可分析如图3所示电路．设在电阻网络中通入恒定电流I，电流从e输入至a输出.设4排横向电阻r中通过

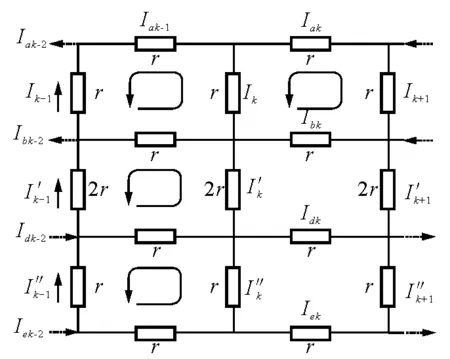
图3 子网络电流参数

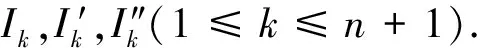
(1)

求解差分方程组式(1)是解决问题的关键.根据文献[1]所采用的矩阵变换新的差分方程组模型，从而间接求解.

将(1)式左乘一个二阶待定矩阵得[1]

(2)

设存在常数t1、t2,使得

(3)

将(3)式展开且根据矩阵相等，则有

(4)

(5)

矩阵方程(1)式可以转化为

(6)

矩阵方程(6)式得差分矩阵方程的特征方程为[1]

(7)

设关于x的方程的两根分别为α、β，关于y的方程的两根分别为γ、δ,则解式(7)得

(8)

(9)

根据文献[3]、[4]解差分方程的方法解式(6)可得

(10)

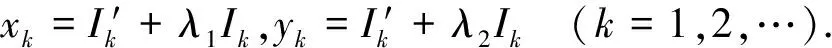
由文献[1]中的边界电流规律：当电流从e输入至a输出时，根据电流的连续性方程由图3、图4可知

(11)

将(10)式分别对k从1到n+1求和并应用式(11)得

(α-β)(1+λ1)I

(12)

(γ-δ)(1+λ2)I

(13)

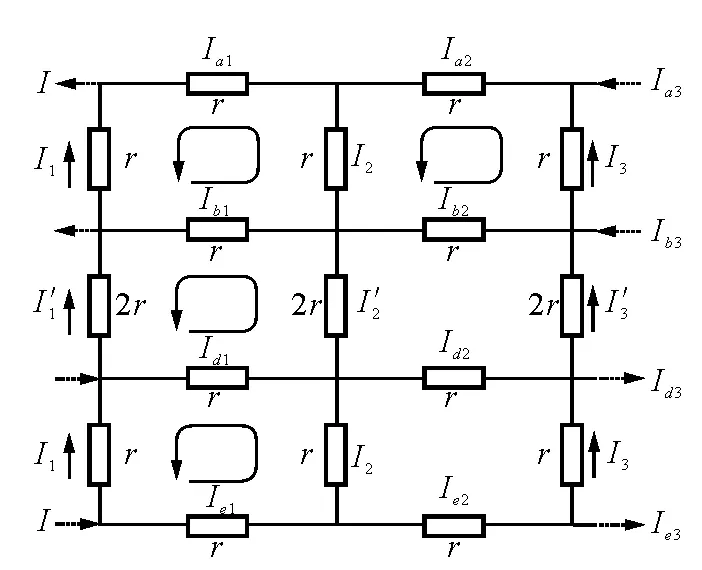
图4 网络边界电流参数

根据文献[3]、[4]的网络分析法,对图4得3×n阶电阻网络进行节点电流分析和网孔电压分析得边界电流参数的差分方程组

(14)

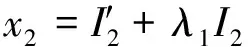
(15)

(16)

所以由矩阵方程式(14)化简整理得[1]

(17)

将(17)式分别代入(12)，(13)式，化简并注意应用(7)式，整理可得如下结果[1]

(18)

由于x1=I1′+λ1I1，y1=I1′+λ2I1，所以式(18)即为3×n阶电阻网络的边界电流规律[1].

3 等效电阻 Rae(n)的一般规律

由文献[1]我们将进一步得出等效电阻的一般规律.因为

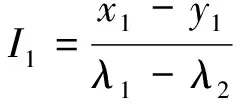
进而有

(19)

(20)

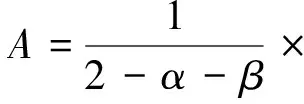
由图4可知，Uae=2I1r+I1′2r，根据欧姆定律

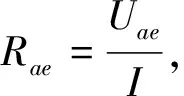
(21)

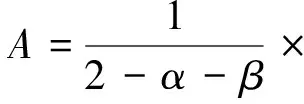
n∈N,α、β由(8)式确定，γ、δ由(9)式确定.(21) 式即为a、e两节点间的等效电阻的通项表达式.

4 无穷网络等效电阻

由(18)、(19)式可以看出[1]

(22)

(23)

当n→∞时

(24)

所以(21)式取极限有

(25)

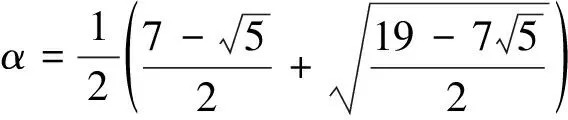
5 模拟实验测量

用NI Multisim 10模拟软件对4×n阶电阻网络进行模拟测量，将n取一系列整数,r取1 Ω.由(25)式计算Rae(n)所得的理论值与模拟实验测量结果如图5所示.

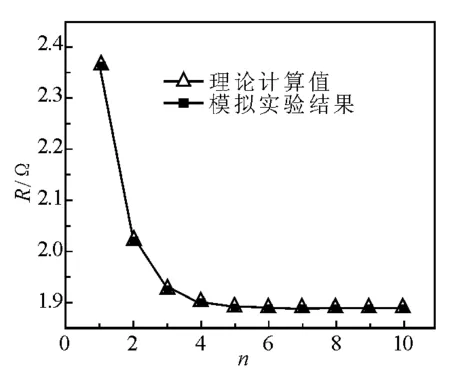
图5 模拟实验结果与理论计算值对比图

从图5可看出，模拟实验测量结果与理论计算结果吻合得很好，说明利用矩阵方法计算n×n阶电阻网络的等效电阻是有效的．

6 结论

利用矩阵变换方法求解了差分方程组,求出有限网络等效电阻Rae(n)和无穷网络等效电阻Rae(∞)的值．然后用NI Multisim 10模拟软件对4×n阶电阻网络在n取一系列的整数值时进行模拟实验测量，实验结果与理论值相当吻合．这一研究说明利用矩阵方法计算n×n阶电阻网络的等效电阻是切实可行的．

参考文献

1 谭志中，方靖淮．3×n阶电阻网络等效电阻的研究．大学物理，2008(9)：7～9

2 曹秀华，谭志中，李颂．构建等效模型研究2×N阶网络的等效电阻．大学物理，2008，27(5)：25～26

3 谭志中，陆建隆，吴国祥．三端梯形网络的等效电阻．河北师范大学学报(自然科学版),2004，28(3)：258～262

4 谭志中，曹秀华，李 颂．2×n阶梯形网络侧端等效电阻的普适规律．南通大学学报(自然科学版),2006，5(2)：10～14