氢原子电子云的三维空间可视化

喻力华 刘书龙 陈昌胜 项林川

(华中科技大学物理学院 湖北 武汉 430074)

氢原子电子云的几率密度分布是“大学物理”教学中的一个重要环节.由于涉及量子力学对微观粒子运动状态的几率诠释，学生在理解上通常存在一定困难．为了清晰和直观地演示氢原子电子云的几率密度，本文通过计算机三维重构给出了电子等几率密度面的三维图形．由于原子间成键的讨论通常参考电子的角向几率密度分布，而电子在三维空间的几率密度分布显然更适合这方面的分析．另外，我们同时绘制了角向几率密度分布的球极坐标表示作为对比．

1 氢原子电子云的几率密度

氢原子中电子的定态波函数在球极坐标系中的表示可以写为两项相乘[1]

ψnlm(r,θ,φ)=Rnl(r)Ylm(θ，φ)

(1)

其中Rnl(r)为径向波函数，Ylm(θ，φ)为角向的球谐函数，n为主量子数，l为角量子数，m为磁量子数．径向波函数和球谐函数的具体形式可参看文献[1]．

电子在体积元dV=r2sinθdrdθdφ内出现的几率为

│ψnlm(r,θ,φ)│2r2sinθdrdθdφ=

│Rnl(r)│2r2dr│Ylm(θ，φ)│2dΩ

(2)

由于径向波函数和球谐函数已被分别归一化，因此径向几率密度为│Rnl(r)│2r2，表示电子出现在r～r+dr球壳内的几率密度;角向几率密度为│Ylm(θ，φ)│2，表示电子出现在dΩ=sinθdθdφ立体角元内的几率密度.│ψnlm(r,θ,φ)│2则为电子在三维空间的几率密度分布．

2 电子三维等几率密度面和角向几率密度的球极坐标表示

本文利用Mathematica软件绘制了氢原子电子云的三维等几率密度面和在球极坐标系中的角向几率密度分布．图1为角向几率密度的球极坐标表示，图2为三维等几率密度面图，绘制图1、2所用的Mathematica函数分别为：SphericalPlot3D，Con-tourPlot3D．

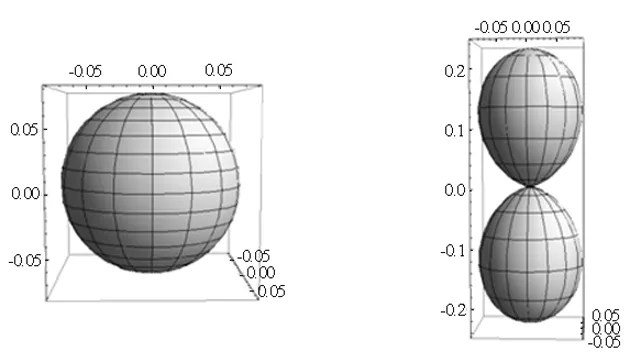
(a)│Y00│2 (b)│Y10│2

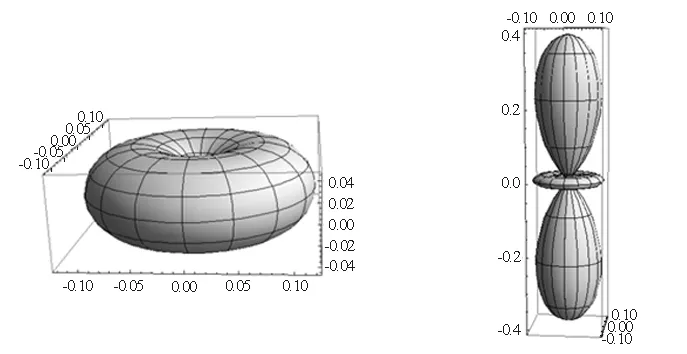
(c)│Y1±1│2 (d)│Y20│2

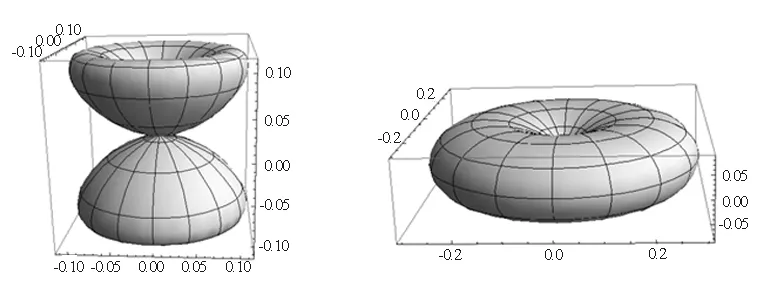
(e)│Y2±1│2 (f)│Y2±2│2

图1 角向几率密度

需要说明，两种图所表示的含义不同.在球极坐标系中的角向几率密度图中，曲面上的某一个点到坐标原点的距离表示其对应方向的角向几率密度大小，而图2的三维等几率密度面则是在三维实空间中，几率密度相等的点所围成的曲面．

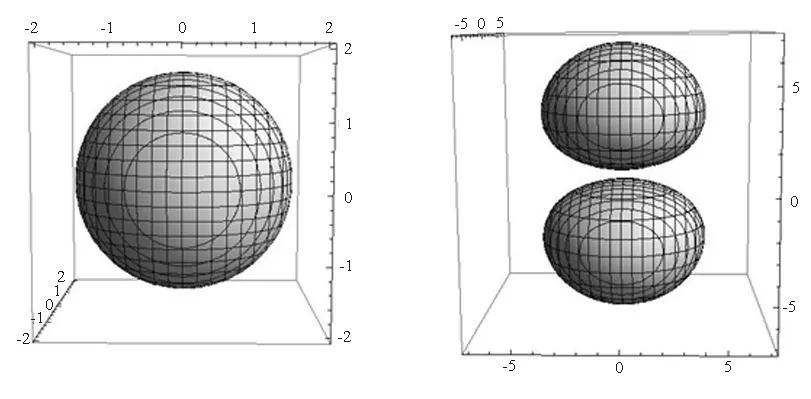
(a)│R10Y00│2=0.01/a03

ΔL=±2a0(b)│R21Y10│2=5×10-4/a03

ΔL=±7a0

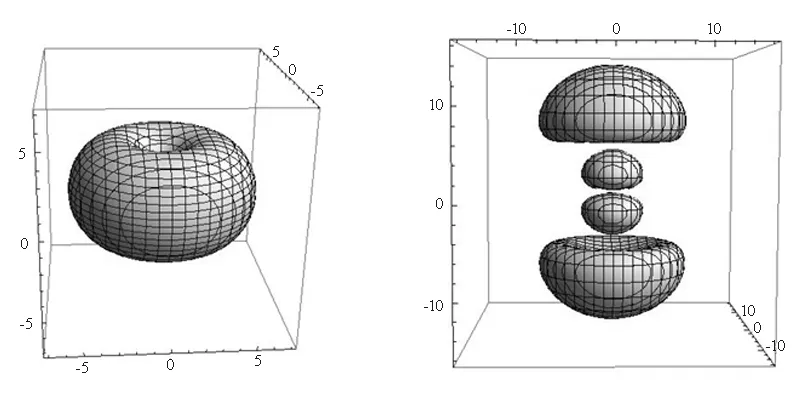
(c)│R21Y1±1│2=5×10-4/a03

ΔL=±7a0(d)│R31Y10│2=8×10-5/a03

ΔL=±16a0

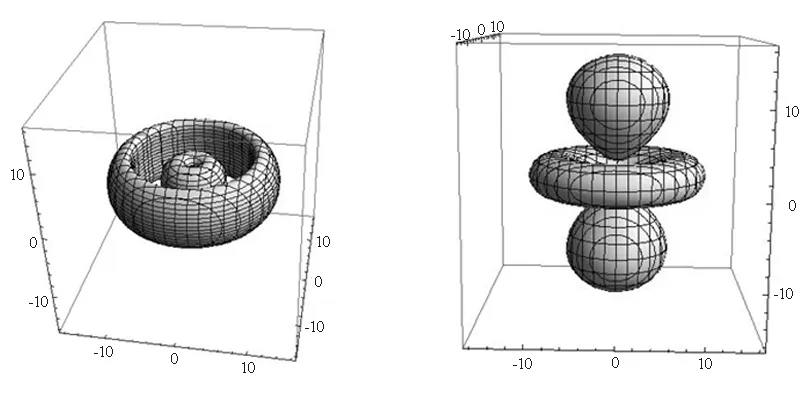
(e)│R31Y1±1│2=8×10-5/a03

ΔL=±16a0(f)│R32Y20│2=8×10-5/a03

ΔL=±16a0

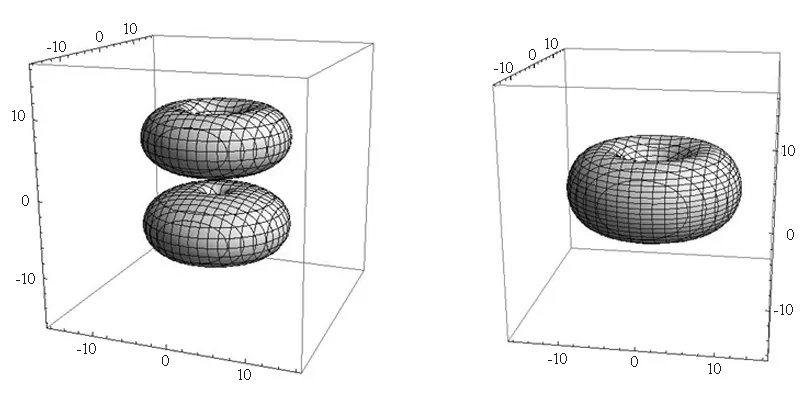
(g)│R32Y2±1│2=8×10-5/a03

ΔL=±16a0(h)│R32Y2±2│2=8×10-5/a03

ΔL=±16a0

图2 三维等几率密度面

在两种图中，z轴均竖直向上，由于氢原子电子的波函数中，φ角只影响相位，几率密度与φ角无关，因此x、y轴可以放置在水平面上的任意两个垂直方向，这也导致无论是角向几率密度分布还是三维等几率密度面，电子的几率密度分布图均关于z轴旋转对称．由于氢原子中电子的不同量子态在实空间的分布范围不同，因此为了得到几率密度的全貌，对于不同的量子态，图2选取的绘图范围可能不同；但每一个图的x、y、z三个方向绘制范围相同，以ΔL标出，其中a0为第一玻尔半径，同时，三维重构所针对的几率密度值也在每一个图中给出．

我们得到的角向几率密度分布图(图1)与文献[1]给出的完全相同，显然球极坐标表示可以很好地说明电子角向的几率密度分布.同时，图2给出的三维空间电子等几率密度面与文献[2]用二维平面阴影表示的几率密度分布也一致．由于氢原子电子的三维空间几率密度分布由径向和角向波函数共同决定，因此，图2一方面能反映图1的角向几率密度分布的特点，另一方面又和径向几率密度相关．例如l= 0的s电子角向几率密度为一个常量，即图1(a)为一球面，则无论径向波函数如何，在三维实空间等几率密度面均为球面，径向波函数只是影响在不同半径处的几率密度值，因此本文只给出了1 s电子的等几率密度面[图2(a)]．在图1(b)、(c)中，l=1的p电子角向几率密度分布特点，在图2(b)、(c)中的2p电子等几率密度面非常好地反映了出来，而在图2(d)、(e)中的3p电子等几率密度面又明显地表现出了径向波函数的一些特点，如径向几率密度在某些半径位置将出现极小节点．另外，在图2(f)、(g)、(h)中，l=2的3d电子等几率密度面也明显地反映了图1(d)、(e)、(f)中的角向几率密度分布，但图2给出的是在三维实空间几率密度分布的直观结果．

通过上述讨论可见，利用数学软件三维重构得到的三维等几率密度面，可以清晰直观地反映电子云的几率密度分布情况，因此可以使学生更容易地理解量子力学波函数的几率诠释，这种方法非常适合于“大学物理”的教学演示．

参考文献

1 曾谨言.量子力学(第四版).北京：科学出版社，2007

2 赵云芳，周战荣，李育新. 氢原子电子云的计算和可视化分析.大学物理，2009，28(9)：51