冲击荷载下套箍系数对铁路桥限高防护架动力响应的影响

鞠翱天,曲淑英,侯兴民,王金田

(烟台大学土木工程学院,山东烟台 264005)

铁路桥限高防护架是对铁路桥进行防护,避免桥下过往车辆对铁路桥的碰撞,从而影响正常的铁路运输。随着我国铁路建设的迅速发展,为保障铁路的安全运营,需要对其施行一系列的保护措施,尤其是铁路下部有机动车辆经过的路段,须进行铁路桥段的保护,以保证铁路运输的正常运行。《铁路运输安全保护条例》明确规定：下穿铁路桥梁、涵洞的道路,应当按照国家有关标准设置车辆通过限高标志及限高防护架[1]。

目前,我国铁路桥防护架主要有钢管、混凝土、钢筋混凝土以及钢管混凝土防护架。混凝土及钢筋混凝土结构防护架施工过程复杂,耗费大量的人力物力,工期较长,抗冲击能力较弱；而钢管与钢管混凝土结构防护架弥补了前者的缺陷,并且对周边环境影响较小,被称为绿色建筑。钢管混凝土结构组合了钢材和混凝土各自的优点,即强度高、自重轻、施工周期短。近年来国内外研究者在钢管混凝土结构动力分析方面进行了大量的研究,尤其是在钢管混凝土结构的轴心受压、轴心受拉等工作性能取得了较好的成果,并广泛地应用于高层和超高层建筑柱、桥梁桥墩、工业厂房柱等工程结构中[2]。但钢管混凝土结构在受扭、受弯以及冲击荷载作用下的研究相对要少,本文用有限元ANSYS/LS-DYNA软件,对钢管混凝土防护架在侧向冲击荷载作用下进行了动力分析,并通过改变内部套箍系数的参数进行比较分析,为设计提供必要的参考依据。

1 有限元模型

本文通过汽车对限高防护架的碰撞模拟结构所受到的冲击荷载,使用ANSYS/LS-DYNA有限元仿真软件,对整个碰撞过程进行模拟仿真分析,考虑到防护架前方设有一系列减速带以及限速标牌,所以汽车到达防护架时处于低速行驶中,本文考虑汽车低速碰撞防护架,材料处于弹塑性阶段。准确地建立有限元模型,合理地进行汽车碰撞防护架动力学分析,进行了几点基本假设：

(1)防护架立柱与地面采用固接固定方式,不考虑土体与结构的相互作用；

(2)防护架内部各个管节点采用焊接连接方式；

(3)汽车模型采用立方体模块进行简化建模；

(4)汽车与防护架的碰撞接触面为防护架横梁的中间位置,并且碰撞方向与防护架之间的角度为90°。

1.1 单元类型

整个模型采用的单元类型均为solid164单元,是一个八节点三维实体单元,由于该单元在模型计算中默认的情况下采用单点积分,容易产生沙漏问题[3]。为了提高计算的精度,本文采用了模型的全积分单元算法。

1.2 结构尺寸及材料

限高防护架立柱直径为219 mm,管壁厚14 mm,高度为4.9 m；立柱支撑直径为121 mm,管壁厚14 mm,长度为1 m；横梁直径为121 mm,管壁厚分别为5、6、7 mm和8 mm,长度为12 m；横梁支撑直径为100 mm,管壁厚分别为5、6、7 mm和8 mm,长度为1 m。钢管选用随动塑性材料模型,与应变率参数有关,钢管弹性模量E=2.0×105MPa,泊松比υ=0.27,密度ρ=7 800 kg/m3,初始屈服应力σ0=3.1×105MPa,切线模量Etan=7.63×102MPa,应变率选用Cowper-Symonds模型,塑性阶段的屈服应力采用与应变率相关的参数表示,如式(1)所示

(1)

在碰撞过程中由于立柱的变形及应力比较小,所以混凝土只填充在横梁及其支撑的钢管内。混凝土材料采用双线性弹塑性模型,模型参数见表1。

表1 混凝土双线性弹塑性模型

汽车模型模块的尺寸为1 m×1 m×2 m,弹性模量为E=2.0×107MPa,泊松比为υ=0.27,密度为ρ=2 000 kg/m3。汽车与防护架碰撞时的速度为5 m/s。

1.3 模型的建立

本文选取汽车模块的单元尺寸为0.2 m,防护架钢管的单元尺寸为0.03 m,核心混凝土的单元尺寸为0.02 m。为了提高分析的精度及效率,需合理地进行网格划分和单元尺寸的选取。接触面采用单向接触类型,选取质量块碰撞面为主面(master),防护架碰撞面为从面(slave),进行从节点对主面的穿透,计算效率高[4]。图1、2分别为防护架与汽车的建模及网格划分图和防护架的变形图。

图1 防护架与汽车建模及网格划分图

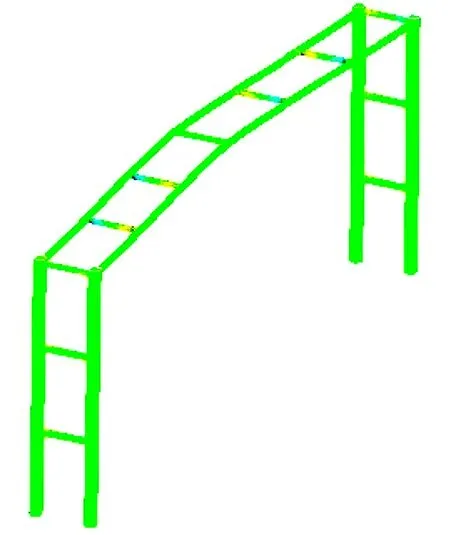
图2 防护架变形图

2 钢管管壁厚度对防护架动态响应分析的影响

钢管混凝土结构的工作性能随着套箍系数物理参数fy和fck以及几何参数α的变化而变化[5],套箍系数综合反映了钢材在钢管混凝土构件中所占的比例,如式(2)所示

ξ=Asfy/(Acfck)=αfy/fck(2)

式中，As为钢管的横截面积；Ac为混凝土的横截面积；fy为钢管的屈服强度；fck为混凝土的标准抗压强度；α为含钢率。

改变了钢管的管壁厚度,即改变了含钢率,在混凝土强度不变的前提下,也就改变了钢管混凝土结构的套箍系数。通过选取4种不同管壁厚度的钢管混凝土防护架,进行汽车碰撞防护架的动力分析,钢管管壁厚度分别为5、6、7 mm和8 mm。核心混凝土的强度为C20。汽车与防护架的碰撞为三维问题,考虑到沿碰撞方向的受力、变形反应要大得多,因此本文只考虑碰撞方向上的动力反应。

2.1 钢管壁厚对碰撞点碰撞力的影响

图3为碰撞过程中碰撞点处碰撞力对于不同管壁厚度的变化曲线。从图中可以看出，4种管壁厚度的钢管混凝土防护架的碰撞力曲线整体趋势变化相同,大致可以分为3个阶段：急剧震荡阶段,震荡稳定阶段,震荡衰减阶段[6]。汽车刚撞击防护架时,碰撞力处于急剧震荡阶段,碰撞力急剧增加,然后至0.07 s附近时刻迅速震荡到零值,0.1 s时刻附近急增到二次较大碰撞力幅值；0.1 s至0.3 s时间段,碰撞力处于震荡相对稳定阶段,围绕碰撞力90 kN附近震荡；0.3 s以后碰撞力处于震荡衰减阶段,开始缓慢震荡到零值。

图3 管壁厚度不同时碰撞力的时程曲线

从达到零值的时间不同可以看出,管壁厚度为8 mm的防护架在0.37 s时刻首先与汽车脱离开,管壁厚度为7 mm的防护架在0.4 s时刻首先与汽车脱离开,管壁厚度为6 mm防护架于0.42 s与汽车脱离,最后是5 mm壁厚防护架于0.45 s附近与汽车脱离,说明管壁厚度越大的钢管混凝土防护架与汽车的碰撞接触时间越短,越最早发生分离。从震荡稳定阶段碰撞力变化曲线可以看出,随着管壁厚度的增加,碰撞力的大小趋势也在增加。比较分析可得：随着钢管管壁厚度的增加,防护架套箍系数也在增大,碰撞力的平均值也会相应增大,并且汽车与防护架相互作用的时间也会减短。

2.2 钢管壁厚对防护架碰撞点位移时程的影响

防护架在碰撞过程中位移最大的点为碰撞接触面中心点,选取该点来进行碰撞动力分析中的位移时程分析。图4为管壁厚度不同时碰撞点位移的时程曲线。从图中可以看出,4种壁厚不同的防护架碰撞点的位移曲线整体趋势相同,从碰撞开始时刻,位移逐渐缓慢增加到最大,即防护架达到了最大幅值,然后防护架反向回弹,最后围绕某一个平衡位置震荡。

图4 管壁厚度不同时碰撞点位移时程曲线

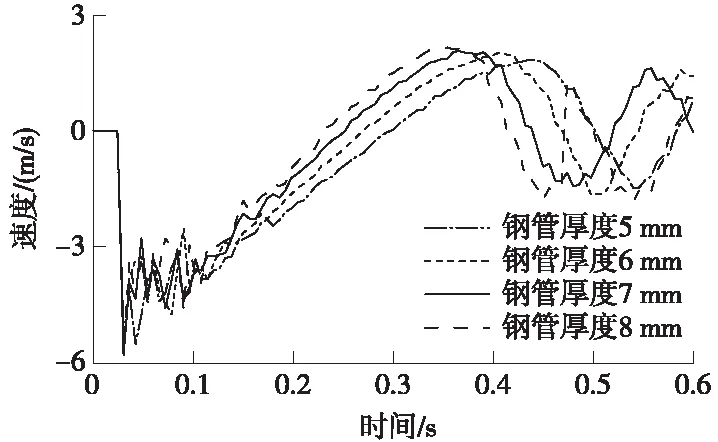
图5 管壁厚度不同时碰撞点速度时程曲线

相比之下,管壁厚度越大的防护架位移值越小,并且最早达到最大位移值。管壁厚度为8 mm的防护架达到最大幅值时刻为0.21 s,之后围绕着0.31 m附近的平衡位置震荡；管壁厚度为7 mm的防护架达到最大幅值时刻为0.24 s,之后围绕着0.36 m附近的平衡位置震荡；管壁厚度为6 mm的防护架达到最大幅值时刻为0.26 s,之后围绕着0.42 m附近的平衡位置震荡；管壁厚度为5 mm的防护架达到最大幅值时刻为0.29 s,之后围绕着0.46 m附近的平衡位置震荡。比较可知：随着钢管管壁厚度的增加,防护架碰撞点的位移最大幅值逐渐减小,说明防护架的位移变形减小,碰撞结束后防护架自身围绕一个位移较小的平衡位置来回震荡。

2.3 钢管壁厚对防护架碰撞点速度时程的影响

图5为管壁厚度不同时碰撞点位移的时程曲线。防护架碰撞点的速度在被碰撞的瞬间达到了最大值,并在0.1 s附近前发生了明显的震荡,之后开始逐渐减小到零,接着反向增大到最大值,最后沿着平衡位置反复震荡。当碰撞过程中速度第一次为零值时,说明防护架在碰撞方向达到了最大位移值,从图中可以看出,8 mm壁厚防护架速度第一次为零值的时间0.21 s,7 mm壁厚防护架速度第一次为零值的时间0.24 s,6 mm壁厚防护架速度第一次为零值的时间0.26 s,5 mm壁厚防护架速度第一次为零值的时间0.29 s,与前面位移时程曲线的数据相吻合,说明防护架在碰撞过程中的数值模拟分析可靠性比较高。

速度时程曲线也可以分为3个阶段：震荡剧烈阶段,震荡稳定阶段,震荡平衡阶段。在0.1 s之前速度时程曲线处于震荡剧烈阶段,速度变化震荡无规律；0.1 s至0.4 s之间处于震荡稳定阶段,速度由碰撞方向较大值逐渐减小到零,然后反向缓慢增大到最大值；0.4 s以后速度处于震荡平衡阶段,防护架在某一平衡位置做简谐振动。分析表明：管壁厚度增加,防护架碰撞点的速度首次较小为零的时间要提前,即防护架更早地达到了最大位移幅值。

3 混凝土强度变化对防护架动态响应分析的影响

选取钢管管壁厚度为7 mm,混凝土强度分别为C20、C40、C60的钢管混凝土防护架,进行汽车碰撞防护架的动力响应模拟分析。

3.1 混凝土强度对碰撞力的影响

图6为碰撞过程中碰撞点处碰撞力对于不同核心混凝土强度的变化曲线。从图中可以看出，不同混凝土强度的钢管混凝土防护架碰撞力曲线整体趋势变化相同,并且数值很接近。汽车刚撞击防护架时,碰撞力急剧增加到接近最大值,然后至0.07 s时刻迅速震荡到零值,0.3 s前围绕碰撞力90 kN附近震荡,0.3 s以后碰撞力开始缓慢震荡到零值。分析可知：钢管混凝土防护架核心混凝土强度改变时,对碰撞力的影响比较小,差异不显著。

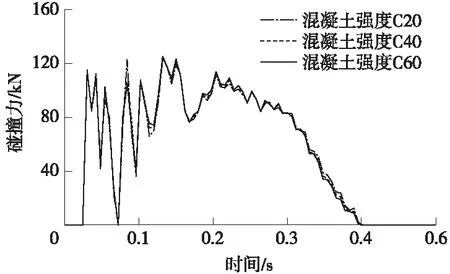
图6 不同混凝土强度下的碰撞力时程曲线

3.2 混凝土强度对防护架碰撞点位移时程的影响(图7)

图7 不同混凝土强度下位移时程曲线

从图7中可以看出,3种不同混凝土强度的钢管混凝土防护架碰撞点的位移曲线整体趋势相同,从碰撞开始时刻,位移逐渐缓慢增加到最大,即防护架达到了最大幅值,然后防护架反向回弹,最后围绕某一个平衡位置震荡。

混凝土强度为C60的钢管混凝土防护架的最大位移幅值为0.56 m,C20钢管混凝土防护架碰撞点的最大位移值为0.58 m,两者相差0.02 m。分析可知：核心混凝土强度的增加会提高结构的抗冲击能力,结构的位移变形会减小,但作用效果比较小。

3.3 混凝土强度对防护架碰撞点速度时程的影响

图8为防护架在不同混凝土强度下的速度时程曲线。防护架碰撞点的速度在被碰撞的瞬间达到了最大值,并在0.1s附近前发生了明显的震荡,之后开始逐渐减小到零,接着反向增大到最大值,最后沿着平衡位置反复震荡。从图中可以看出,不同混凝土强度所对应的速度时程曲线变化差异较小,但却可以发现随着混凝土强度的提高,速度首次减小为零的时间要稍微提早一点。因此,核心混凝土强度增加,会使防护架较早地达到最大位移幅值。

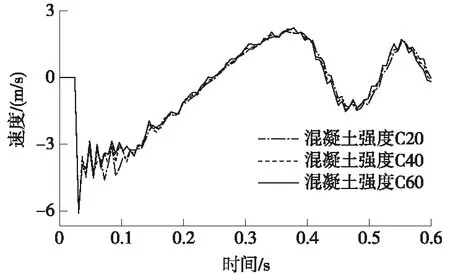
图8 不同混凝土强度下速度时程曲线

4 结论

本文分析了汽车与钢管混凝土防护架的碰撞过程,通过改变钢管混凝土套箍系数,包括改变钢管管壁厚度即含钢率和核心混凝土强度,进行动力分析,得到如下结论：

(1)防护架的位移变形主要集中在横梁及其内部支撑中,尤其是碰撞接触面部位更加显著,随着含钢率的增大,防护架的接触面的位移变形会逐渐减小,能够更好地提高钢管混凝土防护架的抗冲击性能；

(2)随着含钢率的增大,防护架碰撞面达到反弹速度最大值的时间会减小,与汽车脱离的时间会提前；

(3)防护架所受到的碰撞力的平均值随含钢率的增大而增大,并且碰撞力作用的时间随含钢率的增大而减小；

(4)核心混凝土强度的增大,也会引起防护架碰撞面位移变形的减小和碰撞力平均值的增大,但动力分析效果不及含钢率的改变所引起的效果显著。因此增大钢管管壁的厚度,能更有效地提高钢管混凝土防护架的工作性能,更好地保护铁路桥的安全。

[1] 铁路运输安全保护条例[S],2005.

[2] 卢 辉.钢管混凝土动力性能研究新进展[J].世界地震工程,2007,23(4)：119-128.

[3] 薛 量,林忠钦.汽车碰撞数值仿真中的沙漏模态研究[J].机械设计与研究,1999,4∶57-59

[4] 何 涛,杨 竞,金 鑫.ANSYS 10.0/LS-DYNA非线性有限元分析实例指导教程[M].北京：机械工业出版社,2007.

[5] 钟善桐.钢管混凝土统一理论—研究与应用[M].北京：清华大学出版社,2006.

[6] 王 蕊,李 珠,任够平,张善元.钢管混凝土梁在侧向冲击荷载作用下动力响应的试验研究和数值模拟[J].土木工程学报,2007,40(10)：34-39.

[7] 温媛媛,刘亚玲.钢管混凝土构件侧向冲击动力响应的实验研究[J].建筑技术,2009,40(11)：1045-1047.

[8] 康希良,赵鸿铁,薛建阳,仵建斌.钢管混凝土套箍机理及组合弹性模量的理论分析[J].工程力学,2007,24(11)：121-125.

[9] 黄平明,张征文,刘国林,刘柱国.内填式钢管混凝土构件受箍机理分析[J].西安公路交通大学学报,2001,21(4)：43-45.