自适应有限元方法凝固问题模拟的网格各向异性研究
赵达文,李秋书,郝维新
(太原科技大学材料学院,山西 太原 030024)
在凝固过程中,液-固界面上的一些物理现象如界面能、界面动力学具有不同程度的各向异性。理论和实验研究均表明,各向异性对晶体生长形态和生长行为有着决定性的影响[1-3]。通过数值方法模拟凝固组织演化是凝固学研究的热点之一,其中液-固界面追踪是数值求解的难点。近年来出现的相场模型通过引入序参量场,把凝固模型从尖锐界面模型转化为数学上等价的相场模型,从而避免了数值求解中追踪界面的困难,在凝固组织模拟中得到了广泛应用[4]。
相场模型由一个(或组)序参量场、温度场、浓度场的偏微分方程组成,通常通过有限差分或者自适应有限元方法进行数值求解。数值求解过程中首先要把求解区域划分为多个单元组成的网格,这在计算中往往引入额外的各向异性,一般称之为网格各向异性[5]。网格各向异性的存在限制了计算所采用空间步长的大小,同时影响了计算结果的可靠性。因此,必须通过计算确定网格各向异性与计算中各个因素的关系。
由于有限元和有限差分方法微分方程的离散、网格剖分等方面不同,因此二者的网格各向异性行为也存在差异。对于有限差分法的网格各向异性已有研究报道[5],而对于自适应有限元法求解时的网格各向异性尚缺乏研究。因此,本文中通过计算晶体的平衡形态,对自适应有限元求解相场模型时的网格各向异性进行研究。
1 相场模型及求解
这里以纯物质凝固为研究对象,相场模型为[5]:
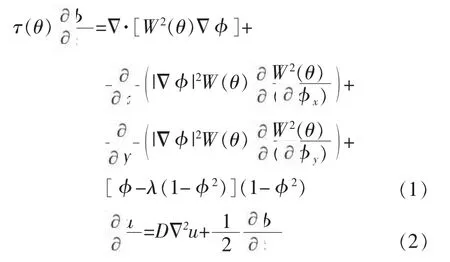
方程(1)是序参量方程,(2)是温度场方程。其中,φ为序参量,u为无量纲温度D为热扩散系数,λ为耦合常数,τ(θ)是界面法线方向与x轴夹角。(θ)为原子弛豫时间,W(θ)为弥散界面厚度。τ(θ)和W(θ)分别对应界面能和界面动力学效应,二者都是与界面法向角θ相关的函数,其具体形式取决于各向异性函数的设定。
这里采用自适应有限元方法求解相场模型,并选择四分树作为动态自适应网格数据结构来建立、调整自适应网格。采用Galerkin加权余量法对相场控制方程进行空间域离散,分别采用向前差分和中心差分格式对序参量场和温度场进行时间域离散。采用非零元素按行压缩方法对其进行存储,同时以ICCG方法迭代求解。具体求解过程见[6]。
2 晶体平衡形态数值算法
处于液-固平衡状态的晶体,其外形由各向异性界面能函数γ(θ)决定。假设晶体中心位于坐标系原点,其外形由以下参数方程给出:
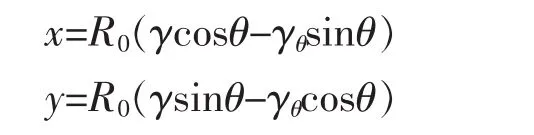
从上式消去 x,y,得:
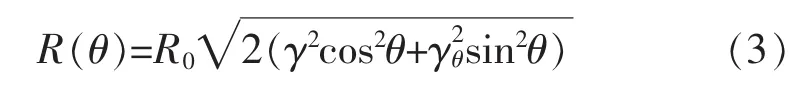
其中,R为界面与原点距离,γθ为界面能函数对θ的导数。
把晶体平衡形态模拟结果代入(3)式,即可得出实际各向异性以及网格各向异性。
由于晶体处于液-固平衡状态,液相和固相温度相同,因此计算中只需要求解相场方程(1)。具体计算过程为:
1)设定输入各向异性系数;
(4)让学生组队进行小组讨论。在课程进行到一定阶段时,组织学生就某一领域的新进展,某一课程重点难点内容,或某个科研成果的案例进行小组讨论,全部过程使用英文,激发学生的学习热情,也提高学生用英文进行学术交流的能力。例如,对2016年诺贝尔化学奖授予的分子机器研究成果分组讨论,激发了学生发散的充满想象力和创新性的点子和思路,课堂气氛热烈有趣,充满生机。
2)设定初始圆形晶核半径;
3)设定计算区域内所有节点温度为-Δ;
4)求解相场方程(1),并计算固/液界面速度V;
5) 如果 V>0,则减小过冷度 Δ 值;如果 V<0,则增大过冷度Δ值;
6)判断V是否小于给定的收敛速度Vcon。如果V<Vcon,则输出平衡界面形态;否则返回继续执行步骤(4);
7)由平衡界面形态依据(3)式求出实际的各向异性值。
计算表明上述算法具有良好的收敛性。图1a)是具有四重对称界面能的晶体形态演化过程。在迭代过程中,〈110〉晶向界面向内收缩,〈100〉晶向界面则向外生长。经过约500次迭代后,晶体形状收敛于平衡形态。图1b)为计算过程中x轴方向的界面速度Vx变化情况,可见随迭代进行Vx迅速趋于0。
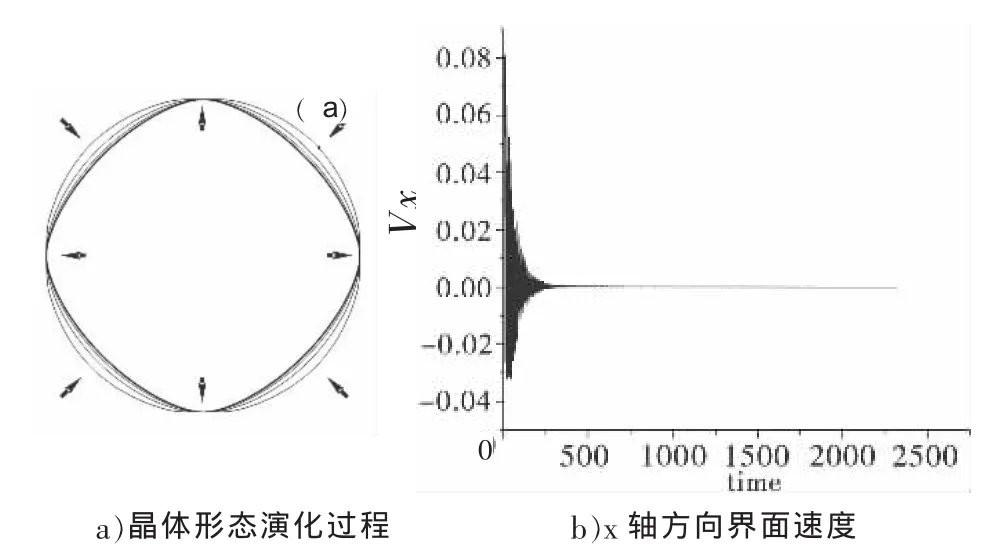
图1 晶体平衡形态相场模拟
3 网格各向异性与影响因素
计算中许多参数的取值都可能影响网格各向异性,其中最主要的影响因素是自适应网格中最细的单元尺寸Δx/W0以及晶核半径R0取值。这里以四重对称性的界面能为例进行讨论,其界面能函数为 γ(θ)=γ0(1+ε4cos4θ)。 计算区域大小为 409.6W0×409.6 W0。
3.1 Δx/W0对网格各向异性的影响
设置 R0=20,ε4=0.05, Δx/W0分别为 0.4,0.8,1.2,1.6,分别计算出实际各向异性系数ε4'。图2为有效各向异性系数ε4'。与空间步长 Δx/W0关系。Δx/W0=0.4,0.8时,二者符合的很好;随着 Δx/W0增大,ε4'和 ε4的差值(网格各向异性)逐渐增大。

图2 实际各向异性系数ε4'与空间步长Δx/W0关系
3.2 晶体半径的影响
设置 ε4=0.05,Δx/W0=0.8,晶体半径 R0分别为10,15,20,25,30,35,40,45,50,由上节计算方法求得实际各向异性系数ε4'。图3为实际各向异性系数ε4'与晶体半径R0关系。在有限差分方法中,R0较小时二者偏差较大,随着 R0的增加,ε4'并逐渐趋近 ε4[5];而在自适应网格中对不同R0时ε4'与ε4非常接近。可见,采用自适应有限元方法可以降低网格各向异性。
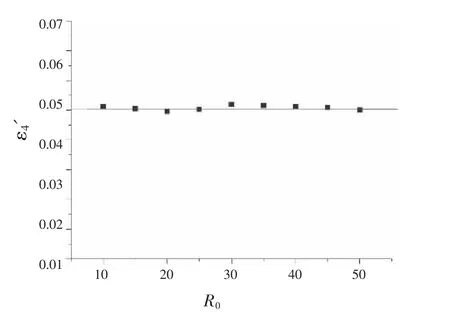
图3 有效各向异性系数ε4'与初始晶体半径R0关系
3.3 网格各向异性与各向异性系数关系
设置 R0=20, Δx/W0=0.8,ε4为 0.00~0.06,由上节计算方法求得不同各向异性值对应的实际各向异性 ε4'。 表 1为不同 ε4取值计算得到的实际 ε4'和网格各向异性 ε4'-ε4。 在 ε4=0.01 时, (ε4'-ε4) /ε4大小为18%,此时网格各向异性的影响必须加以考虑; 随 ε4增加 (ε4'-ε4) /ε4'迅速减小, 当 ε4>0.02 时, (ε4'-ε4) /ε4低于 5%, 网格各向异性的影响已经可以忽略。

表1 计算输入各向异性系数和网格各向异性
4 结 论
通过相场模型模拟晶体平衡状态,标定了自适应网格各向异性以及对相场模拟的影响。计算结果表明,随着空间步长增大,实际各向异性系数和输入的各向异性差值增大;网格各向异性与晶体大小无关;低各向异性下网格各向异性对计算的影响较大,当各向异性大于0.03时可以忽略。
[1]Kessler D A,Levine H.Velocity selection in dendritic growth [J].Phys Rev B,1986,33:7867-7870.
[2]Amar M B,Pomeau Y.Theory of Dendritic Growth in a Weakly Undercooled Melt[J].Euro Phys Lett,1986(2):307-314.
[3]Langer J S.Existence of needle crystals in local models of solidification [J].Phys Rev A,1986,33:435-441.
[4]Boettinger W J,Warren J A,Karma A.Phase-field simulation of solidification [J].Annu Rev Mater Res,2002,32:163-194.
[5]Karma A,Rappel W J.Quantitative phase-field modeling of dendritic growth in two and three dimensions [J].Phys Rev E,1998,57:4323-4349.
[6]赵达文,杨根仓,王锦程.过冷纯物质凝固的相场法的自适应有限元模拟 [J].自然科学进展,2006,16:1009-1015.

