人工鱼群算法在孔群加工路径优化中的应用研究

蔡 芸,周立炜

(武汉科技大学机械自动化学院,湖北武汉,430081)

大量孔的连续加工任务称为孔群加工,孔群加工常见于钣金加工、印刷电路板加工和机械零件加工中。合理规划孔群加工路径,缩短刀具移动路径、减少换刀次数及刀具变向次数,将有助于减少辅助加工时间,提高生产效率,节约成本。

孔群加工路径规划含有典型的旅行商问题(Travel Sale-man Problem,TSP),其解空间存在“组合爆炸”,例如在一块已确定初始位置的工件上加工某类孔(数量为n>2),加工完毕后返回,则其可选路径为条,传统的数学规划方法难以求解。目前已经有学者采用遗传算法、蚁群算法、人工免疫系统算法、禁忌搜索算法等智能计算方法求解了孔群加工路径优化的单目标或多目标问题[1-4]。

人工鱼群算法(Artificial Fish Swarm Algorithm,AFSA)是近年来提出的一种模拟鱼群行为的随机搜索方法,是群智能思想的一个具体应用[5-6]。该算法通过仿真鱼的觅食、聚群、追尾行为快速获得最优解,在解决函数优化、组合优化等问题上都取得了成功。但目前国内外学者还没有将人工鱼群算法应用于孔群加工路径优化的研究。本文尝试对此进行研究,并通过具体实例的算法实现,对比人工鱼群算法与其他人工智能算法的求解效果,以期为讲求实效的生产作业提供更好的理论方法。

1 路径优化的数学模型

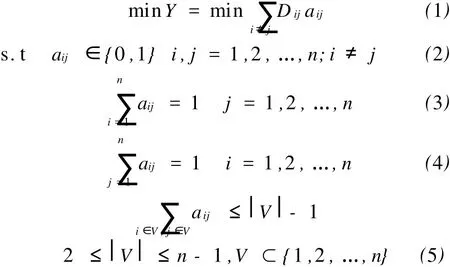
式(1)为目标函数,其中Y表示刀具行进路径长度,Dij为孔i和孔j间已知距离。式(2)～式(5)为约束条件,式(2)表示是否选择孔i到孔j的路径,aij=0时,表示不选择从孔i到孔j;当aij=1时,表示选择从孔i到孔j;式(3)和式(4)表示孔i和孔j的出入只有一次;式(5)约束的是在任何一个孔的真子集中不形成回路[7]。

2 应用人工鱼群算法求解

2.1 符号定义

X:人工鱼群的状态,即被搜索到的最优解状态。X=(X1,X2,…,Xn),其中Xi(i=1,…,n)代表第i条人工鱼的状态,它是孔群加工的序列,这里采用自然数链进行孔序编码,如Xi=(3 2 5 4 7 1 6 9 8),即从孔3出发依次经过孔2—5—4—7—1—6—9—8,然后返回孔3的一条路径。

Yi:对应于Xi的目标函数值,即刀具行进的路径长度,它表示人工鱼当前状态的食物浓度。

Dij:第i条和第j条人工鱼间的距离,它表示两条路径间的差异程度,即两条路径同序列位置的孔序编码差异数目,如Xi=(1,3,2,5,6,4)和Xj=(1,3,6,2,5,4)在路径序列位置3、4、5处的孔序编码不相同,故Dij=3。

Visual:人工鱼的视野范围。

N(Xi,Visual):第i条鱼的视觉邻居集合。

N(Xi,Visual)={Xj|Dij≤Visual}。

式(5)说明，损失规避性购电商的期望效用是(风险中性时的)期望利润和损失规避特性带来的期望效用损失的和。购电商的目标是给定批发价格下，确定最优购电量使其期望效用最大。

δ:表示拥挤度因子,0<δ<1。

FishNum:参与寻优的人工鱼的数目。

Maxgen:最大迭代次数。

Trynumber:人工鱼觅食时最大的试探次数。

Center称为决策变量X1,X2,…,Xm的中心。

2.2 人工鱼群算法的行为描述

人工鱼群算法模拟鱼集群游弋觅食的行为,通过鱼群之间的集体协作使群体达到目的。在AFSA中,每个备选解被称为一条“人工鱼”,多条人工鱼共存,合作寻优(类似鱼群寻找食物)。AFSA初始化为一群人工鱼(随机解),通过迭代搜寻最优解,在每次迭代过程中,人工鱼通过觅食、聚群及追尾等行为来更新自己,从而实现寻优。人工鱼的行为描述如下。

(1)追尾行为:指鱼向临近的最活跃者追捉的行为。人工鱼Xi搜索其视野内的所有伙伴中函数值为最小的伙伴Xmin,如果Yi>Ymin,且Xmin的邻域内伙伴的数目nf满足nf/N(Xi,Visual)<δ(0<δ<1),表明Xmin的附近有较多的食物并且不太拥挤,则向Xmin的位置前进一步,否则执行觅食行为。

(2)觅食行为:指鱼向着食物多的方向游动的一种行为。人工鱼Xi在其视野范围内随机选择一个状态Xj,如果Yi>Yj,则向状态Xj方向前进一步;否则,Xi继续在其视野内重新随机选择状态Xj,判断是否满足前进条件,反复尝试Trynumber次后,如果仍没有找到更优的状态,则执行其他行为。

(3)聚群行为:指每条鱼在游动过程中尽量向临近伙伴的中心移动并避免过分拥挤。设人工鱼当前状态为Xi,探索其邻域内的伙伴数目nf,如果nf/N(Xi,Visual)<δ(0<δ<1),则表明伙伴中心有较多的食物并且不太拥挤,如果此时Yi>Yc,则人工鱼向中心位置Xc前进一步,否则执行其他行为。

2.3 算法步骤

步骤1:设置参数FishNum,Maxgen,Trynumber,Visual,δ;随机产生人工鱼群来初始化X=(X1,X2,…,Xi,…,XFishNum)。m=0,i=0。

步骤2:m=m+1;

步骤.3:i=i+1;对人工鱼Xi执行追尾行为;如发现更好的解Xj,用Xj代替Xi并转到步骤8,否则转到步骤4。

步骤4:圆整Visual×(1-m/Maxgen)获得最近的整数Visual2;如果Visual2>0,转到步骤5并将Visual2应用于其中,否则转到步骤6。

步骤5:对人工鱼Xi,执行觅食行为;如果发现一个更佳的解Xj,则用Xj代替Xi然后转到步骤8,否则转到步骤6。

步骤6:对于人工鱼Xi,执行聚群行为;如发现一个更佳的解Xj,用Xj代替Xi然后转到步骤8,否则转到步骤7。

步骤7:对于人工鱼Xi,随机改变Xi的元素得到新状态Xj。如果它是一个较佳的状态,则用Xj代替Xi并转到步骤8,否则转到步骤3,评价第i+1条人工鱼。

步骤8:更新公告板上的最优化解记录,如果i=FishNum,则转到步骤9,否则转到步骤3,评价第i+1条人工鱼。

步骤9:如果m=Maxgen,输出最优解,程序结束,否则转到步骤2,计算第m+1代人工鱼群。

3 算例分析

3.1 算例的已知条件

为了比较人工鱼群算法与其他智能算法的优化性能,采用文献[1]、文献[3]中的注塑模上模具的孔群加工实例。模具简图如图1所示。已知条件为:26个孔中心的坐标邻接矩阵B=[50,50;50,450;690,450;690,50;100,120;100,380;640,380;640,120;30,150;30,350;710,350;710,150;160,70;580,430;160,150;160,350;580,350;580,150;230,250;300,130;440,130;510,250;440,370;300,370;250,180;490,320]。

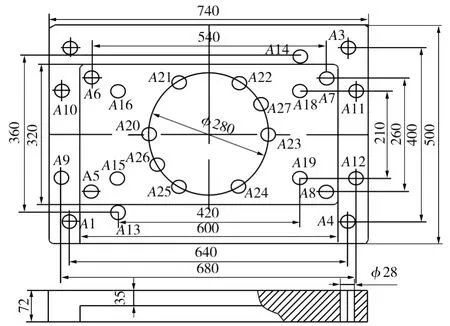
图1 注塑模上模具简图Fig.1 Upper die of in jection mold

3.2 计算结果

当算法参数取FishNum=10,Maxgen=150,Trynumber=150,Visual=8,δ=0.8时,采用配置为Intel Co re 2 Duo E6550,2.0GB RAM的计算机,在MatLabR2010a软件平台上实现的算法程序,需耗时2.28 6 s找到最短路径:1—5—13—15—19—25—20—21—18—8—4—12—11—3—7—14—17—22—26—23—24—16—6—2—10—9—1,其长度为2 696.381 mm,如图2所示。按照传统的孔类型分批加工(按孔的编号顺序加工)的路径总长度为9 449.5 mm[1]。通过人工鱼群算法优化,加工路径缩短为传统加工方式的28.53%。

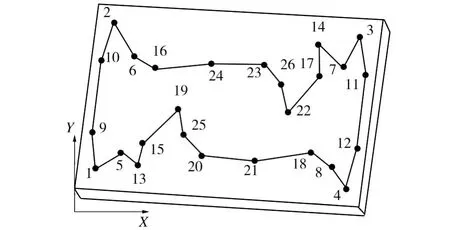
图2 最优加工路径Fig.2 Optimal holes machining path

不同算法的计算结果[1,3]如表1所示。表1中,除改进遗传算法外,其余均为经过100次实验获得的结果。由表1中可见,人工鱼群算法求最优解的效果优于其他几种算法,获得的平均解也是较优的。

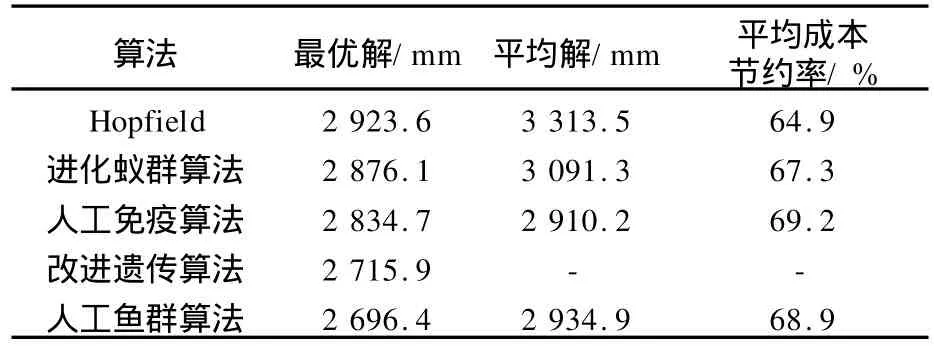
表1 不同算法计算结果对比表Table 1 Comparison of computational results

3.3 算法参数分析

本例使用的算法参数是一个需要优化的问题。笔者在FishNum=10～30,Maxgen=50～200,Trynumber=10～200,Visual=2～10,δ=0.2～1.0的参数范围内进行了一些实验,发现参与寻优的人工鱼数目和觅食探测次数选较大值时,求优效果较佳但耗时。考虑计算时效的情况下,参与寻优的人工鱼的数目选择10较为合适,Trynumber在100～200期间,算法容易收敛,但是不能总是收敛到目前发现的最优值2 696.381。另外,Visual值通常不能取太小,需要大于参与寻优的人工鱼的数目的一半以上,例如,鱼群大小FishNum为10时,Visual取7～8较好。此外,拥挤度因子也不能取得过小,取0.7～0.9时,求解效果较优。

4 结语

本文建立了最小化孔群加工路径的数学优化模型,对基本人工鱼群算法进行了应用改进,对人工鱼觅食过程中的视野范围因子实行了逐代改进的方法,提高了算法的搜索时效。实例计算表明人工鱼群算法能够较好地解决此类问题,在同类算法中有较优秀的表现。由于随机算法的性能同随机初始解以及算法参数的选择关系密切,所以今后还需做大量的数值实验来获取较好的算法参数组合,便于算法的工程实际应用。

[1] 凌玲,胡于进,王青青,等.基于改进遗传算法的孔群加工路径优化[J].华中科技大学学报:自然科学版,2009,37(8):88-91.

[2] Ghaiebi H,Solimanpur M.An ant algorithm for optimization of hole-making operations[J].Computers&Industrial Engineering,2007,52(2):308-319.

[3] 肖人彬,陶振武.孔群加工路径规划问题的进化求解[J].计算机集成制造系统,2005,11(5):682-689.

[4] Kolahan F,Liang M.Op timization of hole-making operations:a tabu-search approach[J].International Journal of Machine Tools&Manufacture,2000,40(12):1 735-1 753.

[5] 李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11):32-38.

[6] 李晓磊,路飞,田国会,等.组合优化问题的人工鱼群算法应用[J].山东大学学报:工学版,2004,64(4):64-67.

[7] 张振普,王大承.群孔加工路径的优化方法[J].五邑大学学报:自然科学版,2008,22(2):25-30.