终端滑模控制器设计在永磁同步电动机中的应用

马 新，平静水

(淮南师范学院 数学与计算科学系，安徽 淮南 232038)

永磁同步电机(PMSM)因其体积小、性能好、结构简单、可靠性高、快速响应能力强、具有高效率及良好的动静态特性等优点，被广泛的应用于高精度位置控制的伺服系统，如在工业机器人、航空航天、数控机床、精密电子仪器设备[1]等电动机性能、控制精度要求较高的应用场合与领域得到了广泛的应用.然而，PMSM的精确的位置控制却由于其速度和电流的非线性耦合以及转矩方程中的非线性而变成一个复杂的问题[2].因此从电机的非线性入手，实现PMSM的高性能控制具有重要的意义.随着现代控制理论的发展，非线性技术逐步应用到电机控制系统中，如Backstepping[3]、反馈线性化[4]、无源性控制[5]方法等，但是这些方法都存在一定的局限性，为了达到精确地位置控制，克服以上方法的局限性，本文将采用新的控制方法——终端滑模控制器，它是一种快速控制机制[6-12]，当系统状态在有限时间内收敛时，它的性能达到理想点.对于强耦合高阶系统，当某些状态在有限时间内达到零时，将对其它状态不再有影响.本文是在文献[11]的基础上利用文献[13]中的数学模型所做的进一步研究.

1 系统描述

以定子d、q轴电流id，iq和转子角速度ω为状态变量，永磁同步电动机的数学模型可表示为

(1)

控制任务:希望通过调节定子的电压ud和uq，使得转子角速度ω在有限时间内达到理想的转子角速度ω*.

定义跟踪误差为x1e=ω-ω*，并记

x2e=iq，x3e=id

则系统(1)可化为

(2)

2 控制器设计

首先取电压输入信号ud为

(3)

其中β>0为一设计参数.由系统(2)的最后一个方程得

(4)

从而，x3e在有限时间T0内收敛到零.于是，当t>T0时，方程(2)变为

(5)

下面引入一个坐标变换使得系统(5)化为可控标准形，使之在新坐标系下更便于设计TSM控制器.定义坐标变换为

(6)

其中y1，y2相应于广义跟踪误差.于是系统(5)可化为

定义

(7)

则V是一种广义的电压输入信号，不具有实际的物理意义.

下面设计V，使得yi(i=1，2)在有限时间内收敛到零.取TSM流形[7]为:

(8)

其中β1为正常数，p1>q1为正奇数，取

(9)

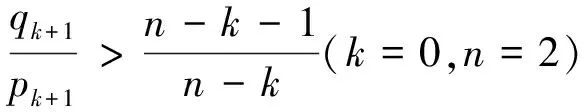
当y1，y2收敛到零时，由可逆变换(6)可知，x1e在有限时间T之后变为零，由x1e的定义可知ω(t)在有限时间内分别完全跟踪理想状态ω*(t).

由(3)、(6)和(7)可求得d轴与q轴电压分别为:

(10)

t>T时，由上述分析易知电压uq为有界的信号.

由上述分析，不难得到如下的定理:

定理1 对于给定的永磁同步电动机系统(1)，设ω*表示理想的转子角速度.电压输入信号uq由(10)式给出，TSM切换面由(8)式给出，则在某一有限时间之后，转子角速度ω将精确地跟踪到理想的转子角速度ω*，跟踪误差达到零并且永远保持为零.且在整个跟踪过程中，闭环系统的所有信号是有界的.

永磁同步电动机系统(1)的TSM控制器的设计步骤如下:

(1)取控制律uq=0，ud如(3)式所示，则x3e在有限时间T0内收敛到零;(2)在T0间之后，取广义电压输入信号V如(9)式所示，则y1，y2在有限时间T内收敛到零，即x1e，x2e在有限时间T内收敛到零.且控制量ud，uq，V在整个控制过程中是有界的.

3 仿真研究

对于给定的PMSM系统(1)，其参数设置如下:定子电阻R1=0.9，电机极对数np=2，d轴等效电感Ld=0.732×10-3H，q轴等效电感Lq=0.216×10-3H，电机转矩常数ψr=0.506Nm/A2，电机转动惯量J=2.99×10-4kg·m2，负载粘滞摩擦系数B=0.035N·m·s/rad，负载有关正的位置常数

TL=4.08N·m.

TSM参数取为:

q=q1=3，p=p1=5，β=β1=5，K=5

初始值为:x1(0)=-1，x2(0)=5，x3(0)=5， 理想的负载速度ω*为:

ω*=πcos(2t)(1-e0.3t3)+0.45πsin(2t)e-0.3t3，

仿真图像如图1所示.其中图(a)和(c)、(d)为跟踪误差和控制律随时间的变化曲线.图(b)为实际转子的速度跟踪理想的转子的速度随时间的变化曲线.由图(a)可知跟踪误差x1e在大约6.5秒时收敛到零，表明通过调节定子的电压Vd和Vq，使得转子速度ω在大约6.5秒时间内达到理想的转子速度ω*.由图(b)可以看出实际转子的速度ω在有限时间(6.5秒)以后可以实现对理想转子速度ω*的完全跟踪.由图(c)表明控制律Vq在整个控制过程中始终是有界的;图(d)表明控制律Vd在t=0.5秒时达到零并永远保持为零.

本文将递推TSM有限时间收敛的控制方法应用于PMSM系统，充分利用了有限时间跟踪控制方法的分析简单，动态响应快，应用广泛等优势，保证了系统状态在有限时间内达到完全跟踪的目的.仿真结果充分显示了该控制策略的有效性.

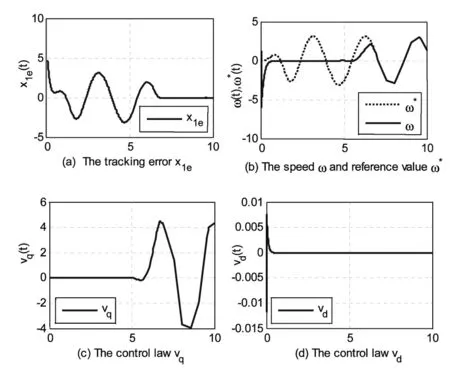
图1 跟踪误差、转子速度和控制律随时间的变化曲线

参考文献：

[1]徐衍亮，唐任远.永磁同步电动机驱动的电动汽车仿真研究[J].系统仿真学报，2004，16(4).

[2]Hemati N，Leu Mi.A Complete Model Characterization of Brushless DC Moto[J].IEEE Trans.on Indus.Appl.，1992，28(1).

[3]李三东，沈艳霞，纪志成.永磁同步电机位置伺服控制器及其Backstepping设计[J].电机与控制学报，2004，8(4).

[4]Baik I C，Kim K H，Youn M J.Robust Nonlinear Speed Control of PM Synchronous Motor using Boundary Layer Integral Sliding Mode Control Technique[J].IEEE Trans.on Control Syst.Technol.，2000，8(1).

[5]Kaddouri S，Akhrif O，LE-HUY H.Adaptive Nonlinear Control for Speed Regulation of a Permanent Magnet Synchronous Motor[C].Proceedings of the 25th Annual Conference of the IEEE Industrial Electronics Society，1999(3).

[6]YU X Y，Man Z H.Model Reference Adaptive Control Systems with Terminal Sliding Modes[J].International Journal of Control，1996，64(6).

[7]WU Y Q，YU X Y，Man Z H.Terminal Sliding Mode Control Design for Uncertain Dynamic Systems[J].Systems & Control Letters，1998，34(5).

[8]郑雪梅，冯勇，鲍晟.非匹配不确定系统的终端滑模分解控制[J].控制理论与应用，2004，21(4).

[9]冯勇，鲍晟，余星火.非奇异终端滑模控制系统的设计方法[J].控制与决策，2002，17(2).

[10]WU Y Q，ZONG G D.Relay Switching Controller with Finite Time Tracking for Rigid Robotic Manipulators[J].Acta Automatic Sinica，2005，31(3).

[11]马新，宗广灯，武玉强.永磁同步电动机的有限时间跟踪控制[J].电机与控制学报，2006，10(5).

[12]马新.一类五阶异步电机模型的有限时间跟踪控制[J].皖西学院学报，2009，25(2).

[13]张波，李忠，毛宗源，等.一类永磁同步电动机混沌模型与霍夫分叉[J].中国电机工程学报，2001，21(9).