钢框架稳定性探讨

周菊根

（广东工程建设监理有限公司，广东 广州 510000）

钢框架稳定性探讨

周菊根

（广东工程建设监理有限公司，广东 广州 510000）

钢框架稳定性的计算主要是柱子稳定性的计算，其中计算长度系数法避免了对结构做整体屈曲分析，因此得到广泛应用。钢框架柱的计算长度系数与多因素有关，体现在初始几何缺陷、荷载条件、节点连接刚度、支撑刚度、层间相互作用和二阶效应等方面。但钢框架的整体稳定判定准则也起着越来越重要的作用。

钢框架；框架柱；计算长度系数；整体稳定性；判定准则

近年来，随着我国国民经济的发展钢结构作为一种快速结构体系得到越来越广泛地应用。钢框架作为主要的钢结构类型，其研究就显得尤为迫切和必要。在钢结构的设计中，稳定性是一个突出问题。如果这个问题处理得不好，将会造成不必要的损失。钢框架结构稳定计算包括框架本身的整体稳定性判定和柱子的稳定性。其中主要是计算柱子的稳定性，即：将框架稳定问题简化为确定柱子计算长度的问题。而对钢框架的整体稳定判定准则的研究现状作一简要回顾。

1 钢框架柱子稳定性计算

框架柱的稳定承载力设计计算公式直接取决于它的计算长度。传统的做法是确定框架柱的计算长度系数。由于该方法是对单个构件进行设计，因此，在概念上简单明了，在设计过程中，又便于根据实际情况对局部构件截面进行调整；同时，在长期的使用过程中，对计算长度系数法表现出来的种种不足，也进行不断的修正和完善。因此，在目前钢框架稳定设计中，计算长度系数法仍具有很大的使用价值。但是，现有的计算长度系数公式都是在一定的假设条件下推导出来的，没有充分考虑影响框架柱的计算长度系数因素，实际上，框架在一定程度上不可避免地与这些假设条件不一致。对简单对称框架而言，计算长度系数的确定并不难，可以采用中性平衡法、转角位移法、刚度矩阵法等进行计算。但对于杆件较多的多跨多层框架结构，问题就变得复杂了。

2 影响钢框架柱计算长度系数的因素

2.1 初始几何缺陷的影响

关于考虑单元的几何缺陷的方法有3种：①单元模型的直接缺陷法；②等效名义荷载法；③进一步降低切线模量法。单元模型的直接缺陷法，就是在结构分析时直接在单元模型中引入一个确定的缺陷值，这就意味着构件的初始状态不再是直线，而是有一个初始跨中挠度或端部的初始倾斜角。等效名义荷载法，就是在结构分析时采用名义侧向荷载施加到结构每层上，来近似表示几何缺陷对结构的影响。框架的几何缺陷可由作用在柱顶的重力荷载的百分比表示，图1的悬臂柱就说明了等效名义荷载法的基本思想。由几何缺陷引起的弯矩M等效于作用在柱底部的PL/500（图1a），由等效名义荷载引起的M等效于αPL（图1b）。这里的α是等效名义荷载的系数，为使图1a和图1b中的M相等，α取为01002，即：对于失稳时有侧移的框架，几何缺陷取为初始倾斜率（图1a），也可用假想荷载01002P作用于柱顶（图 1b）；对于失稳时无侧移的框架，可取柱的初始矢度为 L/1 000，也可用位于柱高度中央的等效名义荷载01004P代替（图2）。进一步降低切线模量法是在结构分析时，未考虑几何缺陷对结构性能的影响而进一步降低材料切线模量的方法。该法相对于直接缺陷法和等效名义荷载法的优势在于不需要确定几何缺陷的方向，应用较方便。

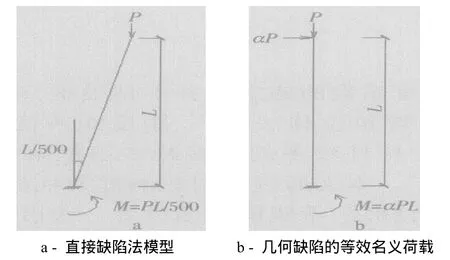
图1 有侧移框架柱的等效名义荷载法的几何缺陷模型

2.2 荷载条件的影响

2.2.1 不对称荷载的影响

《钢结构设计规范》（GB 50017－2003）在条文说明中对单层或多层框架给出的计算长度系数采用了五条基本假定，其中1条是框架中所有的柱子是同时丧失稳定的，即各柱同时达到其临界荷载。按照这条假定，对于单层单跨对称框架来说，符合要求。但是实际结构经常是结构不对称或荷载不对称甚至二者都不对称。若荷载不对称，当左柱承受荷载P而右柱承受αP＜P时（图3），则左柱趋于先失稳。

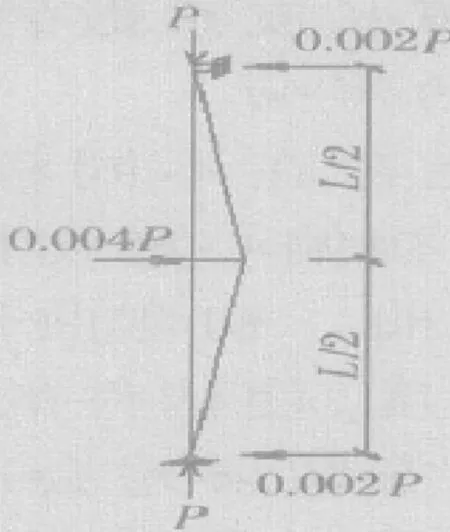
图2 无侧移框架柱的几何缺陷的名义荷载法

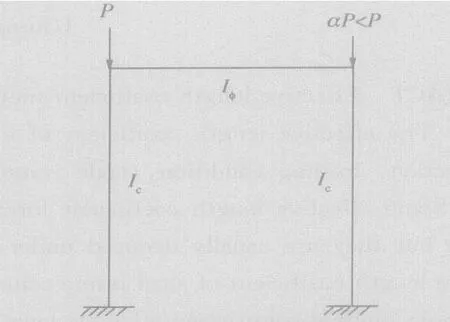
图3 非对称荷载作用模型

但是，左柱失稳而侧移时必然会带动右柱一起侧移，而右柱这时还未达到临界状态，必将对侧移起阻碍作用，从而使左柱推迟失稳。由于整体性，左柱得到右柱的支持，它的计算长度相应减小，P的临界值将有所提高，则左柱的计算长度相应减小。另外，右柱要对左柱提供约束，它的任务加重，计算长度系数大于规范给出的数值，其结果是两根相同的柱在不同荷载作用下同时失稳。

2.2.2 作用在梁跨度上的荷载的影响

在框架柱计算长度系数推导中，假定框架只在梁柱连接点承受竖向轴向荷载，因而柱失稳前没有弯矩，且梁不承受轴力。但实际结构中一般都是梁上作用有荷载，从而会使梁和柱都受弯，由此而引起的支座反力会使梁受压。除此之外，结构还时常承受水平荷载使柱弯曲和侧向移动。如果将作用在梁跨度上的荷载集中到梁端，忽略了框架屈曲前变形和梁的轴线压力，会对荷载的临界值造成一定的误差。有资料表明，分布于梁上的荷载对单跨框架对称失稳时的影响比较大，而对反对称失稳时的影响不大。所以，对于单跨框架反对称失稳时，就可以忽略其梁上荷载的弯矩影响。但是，如果框架顶部有水平支撑防止侧移，会使框架对称失稳，因而要考虑梁上荷载的弯矩影响。

2.3 节点连接刚度的影响

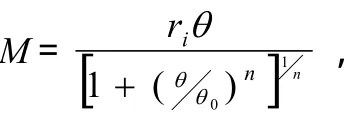
2.4 支撑刚度的影响

柱的计算长度与柱端约束条件有关，除此之外，还与其支撑刚度有关。欧洲建筑钢结构协会在钢结构稳定手册中规定：支撑刚度大于等于5倍的结构本身的侧向刚度时，按无侧移屈曲计算，不足5倍时一律按有侧移屈曲计算。大多数规范中都有关于有侧移和无侧移框架柱的计算长度系数的图形或表格供计算设计使用。但是弱支撑框架柱（框架柱的支撑刚度不足以使框架柱按无侧移屈曲，但又非完全无支撑）的计算长度系数没有包含在规范中。这样，对于非对称框架结构或有倾斜柱的框架结构，按照规范所列表格进行设计会导致自相矛盾的结果。

2.5 层间相互作用的影响

框架结构中柱子并不是独立存在的，而且柱子的边界条件也不是固接、铰接、自由等理想的状况，柱子的端部要受到与它相连的其他构件的弹性约束。框架有侧移失稳时，单根柱总是与同一层的其他柱同时失稳，不会单独失稳，即同一层柱的柱间存在相互作用，该方面已有相关研究，并在此基础上改进了柱计算长度的公式。同样，失稳时，层与层之间也存在着相互作用，这种相互作用主要通过对梁提供的约束在上下各层柱之间按需分配来实现。如果某层柱子失稳趋势很弱，即此柱不仅需要得到梁的约束，甚至还可以对相邻柱子提供转动约束。Bridge和Fraster（1986）对无侧移框架进行了研究，提出了一种迭代法，并给出了柱端约束为负值时（指柱子对相邻层柱子提供约束的情况）计算长度系数诺模图；Kishi和Chen等（1997）则在考虑两者连接半刚性的情况下，对如何确定层与层相互作用进行了研究；Hellesland 和Bjorhovde建议用一种“Method of Means”的方法来考虑有侧移和无侧移框架的层间相互作用；Wood提出了一种刚度分布法，即确定每个柱端的旋转刚度，建立求解临界荷载的节点弯矩平衡方程；梁启智总结了一种简单的方法，首先确定薄弱柱，由其他层提供给薄弱柱两端的有效旋转约束，可分别通过由最上层逐层计算到薄弱层和由底层逐层计算到薄弱层来确定，这样薄弱层的临界荷载就确定了；童根树和王金鹏提出了一种新的确定单跨对称框架柱的计算长度；提出了考虑层间相互作用的较精确的计算框架柱计算长度的方法，即：对于两层框架，通过求解一个一元二次代数方程，得到各柱柱端的转动约束；而对于3层框架，通过求解一个一元三次代数方程，得到各柱柱端的转动约束。

3 钢框架的整体稳定判定准则

在我国《钢结构设计规范）（GB50017－2003）中，对钢框架的整体稳定仍没有明确指出，只是在框架结构的内力分析中做了以下规定：①对某些框架结构宜采用二阶弹性分析，此时应在每层柱顶附加一水平力 H。②对无支撑的纯框架结构，可以在各杆件端的弯距M附加一二阶效应增大值。从这两条规定来看这本规范的思路仍是构件层次的。

在我国新颁布的《高层民用建筑钢结构技术规程）（JGJ99－98）中，对于高层钢结构的整体稳定和判定准则是这样表述的：①对于有符合柱平均长细比和轴压比要求，或不符合按一阶弹性计算所得的侧移要求的结构，可按推荐方法验算整体稳定。②高层钢结构第一阶段抗震设计的层间侧移标准，不得超过结构层高的1/250。第二阶段抗震设计的层间侧移不超过层高的1/70：从这里可以看到，这本规程已明确提出结构整体稳定的概念，并指出其判定准则是层间侧移判定准则。

通过对整体稳定及整体稳定判定准则的相关问题进行研究和统计。发现对钢框架整体稳定研究成果很多，而对于整体稳定判定准则问题研究却不够充分。基本上有3个观点：①荷载－位移曲线顶点判定准则。即当结构某层（一般是顶层）的荷载－位移曲线达到其顶点时即认为此时为稳定临界状态。②承荷极限判定准则。即当结构一定情况下，以缓慢的速度比例加载，达到其最大值时即认为此时为稳定临界状态。③荷载－位移曲线切线斜率判定准则。当其曲线斜率为零时达到稳定临界状态。

4 结束语

综上所述，框架的整体稳定性判定准则在力学和数学上都有其理论依据，是比较严格的判距，但也有以下几方面的不足：①钢框架整体稳定问题全过程分析牵涉到几何非线性和材料非线性，计算工作量较大，传统判定准则一定要全程计算至下降段，对设计分析不必要。②考虑到荷载和材料的随机性，应用传统判定准则作为设计时的准则不安全。③现在研究钢框架整体稳定问题所用的荷载－位移曲线图都是标准框架的顶层节点曲线图。考虑到设计中的非标准框架整体稳定问题，传统判定准则是不准确的。

Steel Frame Stability Discussion

Zhou Jugen

The steel frame stable computation is mainly the pillar stable computation, the effective length method of correlates avoided making entire to the structure the body flexure analysis, therefore obtained the widespread application.Steel frame trestle effective length coefficient with multi－factors related, manifests in initial geometry flaw , the load condition, the joint connection rigidity, the support rigidity, the level aspects and so on interaction and second－order effects.But steel frame’s whole stable the determination criterion is also playing more and more vital role.

steel frame; frame trestle; effective length coefficient; overall stability; determination criterion

TU391

A

1000－8136（2011）06－0013－03