316L不锈钢表面纳米化残余应力对疲劳的数值分析*
程国锋,钟蜀晖,杨昌树
(贵州大学土木建筑工程学院,贵州 贵阳 550003)
316L不锈钢表面纳米化残余应力对疲劳的数值分析*
程国锋,钟蜀晖,杨昌树
(贵州大学土木建筑工程学院,贵州 贵阳 550003)
高速旋转丝表面纳米化是一种新型的表面纳米化方法,对 316L不锈钢表面进行纳米化处理,测定残余应力在材料内部的分布。通过数值模拟分析比较,表面纳米化处理可以提高材料的疲劳极限。
高速旋转丝表面纳米化;残余应力;数值模拟分析
高速旋转丝表面纳米化是一种新型的表面纳米化处理方法,其可以让金属表层晶粒达到纳米量级,晶粒重新排列,间隔距离缩小,相互作用力增强,从而使得材料力学性能得以提高。然而这种处理方法会使材料内部的残余应力重新分布,这又会引起材料整体力学性能发生变化,尤其是对材料的疲劳极限,影响更为显著。本文对316L不锈钢原试件和表面纳米化试件残余应力在材料内部的分布测定,用数值模拟的方法,分析残余应力对材料疲劳极限的影响。
1 实验材料
目前材料表面纳米化处理的方法有3种:分别为表面涂覆或沉积方法、表面自身纳米化方法和混合纳米化方法。在这3种纳米化处理方法中只有表面自身纳米化处理方法,既可解决纳米晶体层与基体之间结合的问题,又可以利用传统的表面加工技术得以实现。本文就是利用这种表面纳米化方法的优越性,利用高速旋转丝表面纳米化方法,在316L不锈钢表面获得纳米层。
本实验采用表面纳米化处理和表面未纳米化处理的 316L不锈钢,其厚度均为5 mm,其材料属性见表1、表2。

表1 316L不锈钢常规性能表
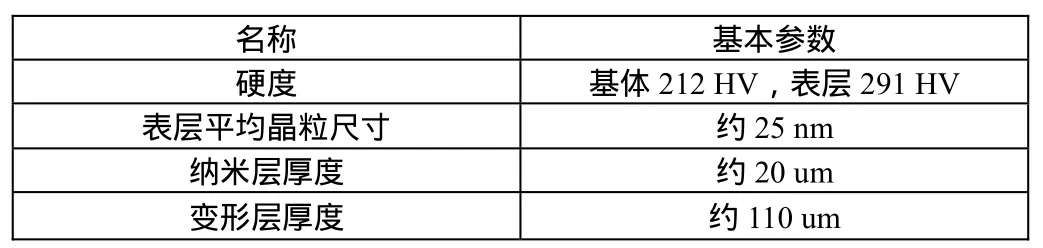
表2 316L不锈钢表面纳米化处理试件的基本参数
2 残余应力的测定及修正
2.1 测试方法的确定
本实验利用X-350 X射线衍射仪测定残余应力,其理论成熟、测量精度高,测量结果准确、可靠,被广泛的运用于机械工程和材料科学。但X射线的穿透能力仅为10 um左右,所测得的只是工件表层的应力。本实验研究残余应力在体内的分布,即需要测定沿材料厚度方向不同层面上的残余应力,这就需要将待测面剥露至表面。故采用逐层剥离法,将待测面剥离至自由面,逐层测定各层面上的残余应力。
2.2 X-350型应力测定仪测试参数的确定
对316L不锈钢板进行残余奥氏体测定,结果Aγ=92.3%,可根据奥氏体的材料性质选定实验参数,其数据选择见表3。
2.3 残余应力的测定
在测验前需对所测的点进行标定,保证所测数据是同一点在不同深度的分布,同时可以用算术平均值来估算所测层面的平均残余应力见表 4。每层表面确定 5个点进行测量,测点分布见图1。

表3 X-350 X射线衍射仪参数选取表
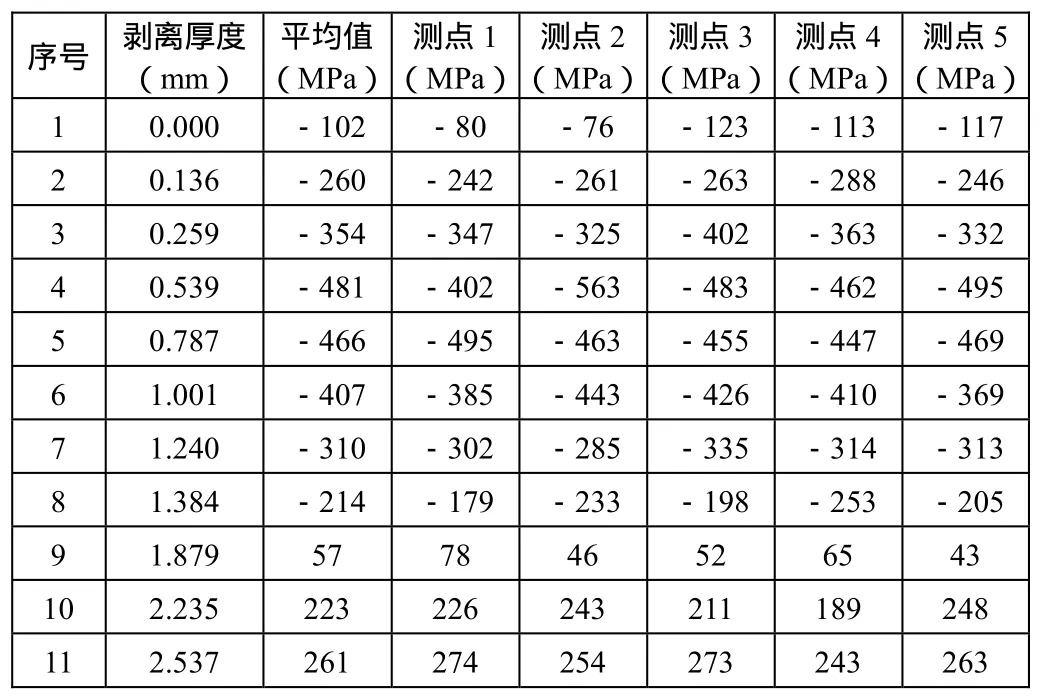
表4 表面纳米化试件残余应力测定结果表

图1 残余应力测点分布图
2.4 残余应力的修正
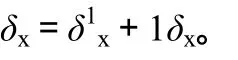
2.5 残余应力测定值修正结果

表5 表面纳米化处理未疲劳试件残余应力修正结果
3 ANSYS疲劳数值模拟分析
3.1 表面未纳米处理模型分析
3.1.1 结构单元选择
结合本实验试件的特征,本次疲劳分析采用有限元单元为SOLID-45单元,该单元用于结构三维实体结构,单元通过8个节点来定义,每个节点有3个沿着XYZ方向平移的自由度。
3.1.2 实体模型建立
316L不锈钢的有限元分析模型根据实验标准试件模型进行建立,其几何尺寸见图2。

图2 实体模型形状尺寸图
本实验试件分为两种,分别为表面纳米化处理试件以及表面未纳米化处理试件。
表面未纳米化处理试件:整个试件表面和内部的晶粒结构基本一致,故性能也一致,建立模型时考虑整个模型为同一材质,作为一个整体。
3.1.3 定义材料特性
316L不锈钢的弹性模量E=191 GP,泊松比λ=0.3。
3.1.4 单元网格划分
根据试件的形状,在中间收缩的弧段将产生应力集中现象,两边的矩形被疲机夹头固定,因此受疲劳的作用较小。故在网格划分时,将收缩的弧段划分为45等份,矩形部分在纵线及竖向划分为10等份,弧段和矩形交接的直线划分为15等份,沿试件厚度方向划分为6等份。
3.1.5 加载并设置荷载步
本疲劳实验R=-1,最大拉应力为210 MPa,最大压应力为210 MPa,故要分为两个荷载步加载:①施加压应力-210 MPa,并设置为第一个荷载步;②施加拉应力,并设置为第二个荷载步。
3.1.6 求解计算(略)
3.1.7 疲劳设置、分析
后处理模块POST1,对求解的结果进行逐步的读取,查看模型应力分布图,进行疲劳设置及分析。
(1)对第一个荷载步进行读取。
(2)第一荷载步疲劳设置。在读取第一荷载步后,进入Main Menu / General postproc / Fatigue进行疲劳设置。①对SN曲线进行设定。本次 316L不锈钢疲劳实验只测得实验频率H=10 Hz,应力比R=-1,最大应力为10.5 kN,而没有对SN曲线进行实验确定,故采用中科院卢柯工作组R=-1的316L不锈钢疲劳实验应力寿命S-N曲线;②疲劳应力的储存。
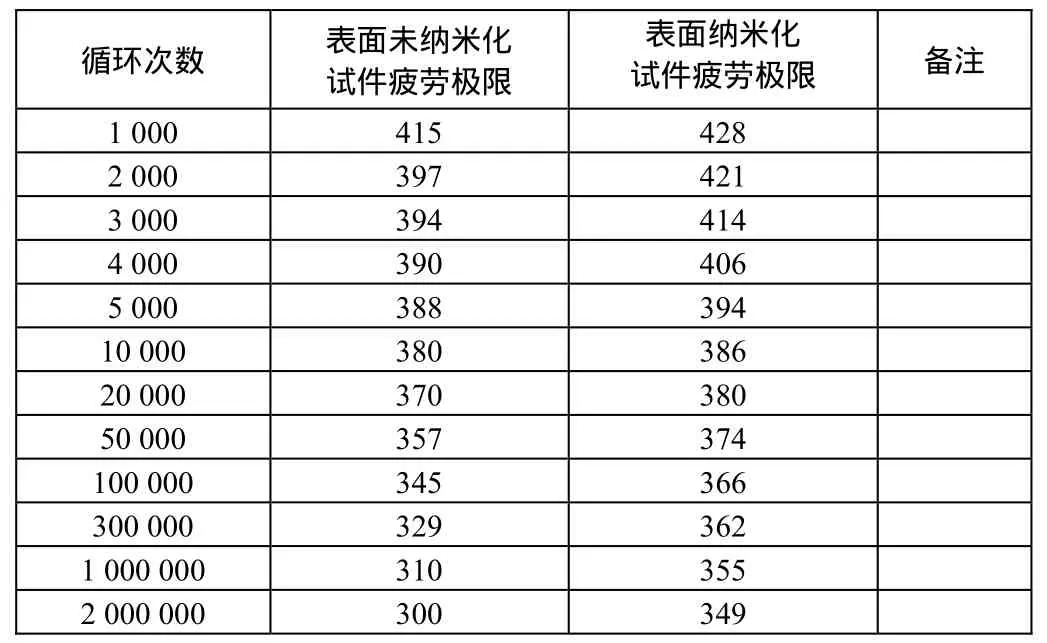
表6 316L不锈钢表面纳米化处理试件R=-1的S-N数据表
(3)对第二个荷载步进行读取。和第一个荷载步读取的方法一样,进入Main Menu / General postproc / Read results读取第二荷载步。
(4)第二荷载步疲劳设置。
(5)疲劳分析:①定义疲劳分析事件和设定疲劳分析次数;②激活疲劳计算,输出疲劳计算结果。

表7 疲劳分析计算结果表
可以得出,316L不锈钢表面未纳米处理试件,在R=-1,最大荷载为10.5 kN的疲劳作用下,疲劳寿命关键点2 347号节点的疲劳寿命Nf=144 000;在距2347号节点有一定距离的43号节点,疲劳寿命Nf=176 600。这表明拉压疲劳在不同的点处产生的应力是影响疲劳寿命的决定性因素。
3.2 表面纳米化处理模型分析
3.2.1 结构单元选择
分析采用有限元单元为SOLID-45单元。
3.2.2 实体模型建立

图3 表面纳米化试件模型形状尺寸图
表面纳米化处理试件:试件表层经过高速旋转丝纳米化处理,其表层晶粒结构和心部结构有差异,故设置2种属性的材料,即表面纳米层和基体层,通过电镜观察,纳米层厚度为20 um,变形过渡层厚度为110 μm。
本课题研究残余应力对材料疲劳性能的影响,故逐层测定了残余应力在材料内部的分布。在数值模拟时,考虑材料内部残余应力对材料性能的影响,因此对材料进行沿厚度方向的划分,在各个层面上施加测定的残余面应力,再整体分析残余应力对材料疲劳性能的影响。
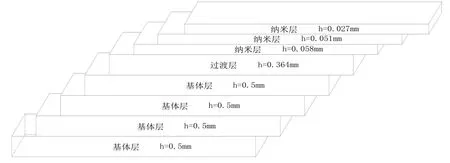
图4 模型分层图(形状对称,只表示一半图形)

图5 表面纳米化试件ANSYA建模图(12层)
3.2.3 定义材料特性
316L不锈钢的基体层材料弹性模量E=191 GP,泊松比λ=0.3。
3.2.4 单元网格划分(略)
3.2.5 施加各层面荷载(残余应力在不同表面的施加)
根据测定残余应力在各个层面的分布,在分层模型的各表面上施加面荷载,模拟残余应力在材料体内部的分布,应力分布值见表8。

表8 残余应力沿模型厚度分布表
残余应力逐层施加图,见图6。
3.2.6 施加疲劳拉压荷载
和原试件的施加,施加方法和未纳米化模型施加的方法一致。
3.2.7 求解计算
3.2.8 疲劳设置、分析

表9 疲劳分析计算结果表
从分析结果可以得出,316L不锈钢表面纳米处理试件,在R=-1,最大荷载为10.5 kN的疲劳作用下,疲劳寿命关键点13015号节点的疲劳寿命Nf=263 400;在13016号节的疲劳寿命Nf=263 900。

图6 残余应力逐层施加图
3.3 数值模拟结果分析
ANSYS数值模拟分析对表面纳米化和表面未纳米化 316L不锈钢试件的疲劳寿命进行分析,表面未纳米化试件模型的疲劳寿命为144 000,表面纳米化试件模型的疲劳寿命为263 400,表面纳米化试件的疲劳寿命是表面未纳米化试件的1.83倍,即经过表面纳米化处理,试件的疲劳寿命提高了83 %。模拟分析表明,试件表面经过纳米化处理后,其疲劳性能大幅度的提高。
4 结论
表面纳米化处理使表面层晶粒细化,晶粒间距缩小,晶粒之间的相互作用力增强,表层的较高作用力阻滞了裂缝在表面的萌生,并且使材料内部的残余应力重新分布。通过数值模拟分析,表面纳米化处理的试件疲劳强度提高了83%。说明表面纳米化处理是提高材料疲劳性能的有效措施。
1 张定铨.残余应力对金属疲劳强度的影响[J].理化检验-物理分册,2003(6):231~235
2 洪京京.316L不锈钢高速旋转丝变形表面纳米化疲劳性能的研究[D].贵州大学,2010
3 高镇同.疲劳应用统计学[M].北京:国防工业出版社,1986:130~135
4 中华人民共和国船舶行业标准 GB3395-92.残余应力测试方法:钻孔应变释放法[S]
5 李红云、赵社戌.ANSYS10.0基础及工程应用[M].北京:机械工业出版社,2008.6
6 何家文、徐可为等.Chin.J.Met.Sci.Technol, 1988:98~102
316L Stainless Steel Surface Nanometer Residual Stress to Weary Numerical Analysis
Cheng Guofeng,Zhong Shuhui,Yang Changshu
The high speed revolving dial indicator surface nanometer is one new superficial nanometer method, carries on nanometer place to the 316L stainless steel surface the principle, the determination residual stress in the material internal distribution.Through the numerical simulation analysis comparison, a superficial nanometer processing may enhance the material the limit of fatigue.
high speed revolving dial indicator surface nanometer; residual stress; numerical simulation analysis
TG174.4
A
1000-8136(2011)06-0001-03
贵州大学研究生创新基金资助项目(编号:校研理工2010047)

