关联规则挖掘算法的多核并行优化*

吴华平，郑晓薇，张建强

（辽宁师范大学 计算机与信息技术学院，辽宁 大连 116081）

关联规则挖掘算法的多核并行优化*

吴华平，郑晓薇，张建强

（辽宁师范大学 计算机与信息技术学院，辽宁 大连 116081）

分析了并行关联规则挖掘算法存在的不足，提出了一种改进的关联规则挖掘的多核并行优化算法。该算法对Apriori算法的压缩矩阵进行了改造，并在多核平台下利用OpenMP技术和TBB技术对串行程序进行循环并行化和任务分配的并行化设计，最大限度地实现并行关联规则挖掘。

关联规则；Apriori算法；频繁项集矩阵；OpenMP；TBB；多核并行

海量数据中隐藏着大量的不为人知的模式和知识，寻找有价值的数据模式和知识是数据挖掘研究的主要内容[1]。关联规则的挖掘是数据挖掘中的一项重要的基础技术。经典的关联规则挖掘算法主要有Agrawal等提出的基于Apriori算法的频繁集方法，该算法以递归统计为基础，以最小支持度为依据剪切生成频繁集。随着数据容量的增加，为了提高关联规则的挖掘效率，研究人员提出了并行挖掘算法[2-3]。这些并行算法都是基于MPI和机群系统实现的，虽然具有速度快、容易实现、要求各节点间同步次数较少等优点，但仍然存在着可扩展性差、网络通信量大、负载不平衡、处理器空转、规则合成难度高等缺点。

目前市场上多核处理器已成为主流，比较有代表性的支持多核处理器的并行计算平台之一的线程构建模块TBB（Thread Building Blocking），可以在其他多核化工具支持下对串行程序中的可并行化部分进行线程的并行化重构，提升多核处理器平台的效能，简化应用程序的并行化过程。本文针对TBB的多核并行编程的优势，结合OpenMP并行编程，提出了一种改进的关联规则挖掘多核并行优化算法。该算法对Apriori算法的压缩矩阵进行了改造，只需扫描一次数据库，并利用TBB技术最大限度地压缩矩阵，使矩阵的运算规模逐步减小。它不需要Apriori算法中的自联接和剪枝，直接通过支持矩阵行向量的按位“与”运算并行地找出频繁集，减少了数据移动带来的额外开销，提高关联规则挖掘效率。与分布式系统的Apriori并行算法相比，该算法采用多核TBB并行技术，不存在节点间的通信与同步、负载平衡和规则合成难度高等问题。实验证明该算法具有高效的并行挖掘效率和较高的多核CPU利用率。

1 挖掘关联规则的串行算法

关联规则的核心是基于两阶段频繁项集思想的递推算法。发现频繁项集是关联规则挖掘应用中的技术和步骤。支持度和置信度是关联规则挖掘中的两个重要指标，为了计算支持度，需要访问数据库。而Agrawal等人提出的挖掘关联规则串行算法Apriori是首先扫描数据库，计算每个数据项的支持度，并根据支持度阈值产生频繁 1-项集 L1；L1用于找频繁 2-项集 L2，L2而用于找L3，如此逐层迭代的搜索，直到不能找到频繁k-项集。Apriori算法存在一些难以克服的缺陷：（1）可能产生大量的候选项集，没有排除不应该参与组合的元素；（2）多次扫描数据库，大大增加系统的 I／O开销，并且数据库有些可以删除的项或事务被多次扫描；（3）连接程序中相同的项重复较多。针对Apriori算法的缺点，参考文献[4]将事务数据库转换为基于内存的矩阵，在矩阵上找出所需的频繁项集，从而大大减少了数据库的扫描次数，但没有对矩阵进行压缩。参考文献[5-6]对矩阵进行了压缩，但不彻底，而且矩阵数据结构不合理，还额外增加了转置矩阵。

本文介绍一种改进的基于Apriori算法的挖掘关联规则的多核并行优化算法。本文改进了参考文献[4-5]中的矩阵的数据结构：在一个单纯的事务矩阵中，添加2个辅助行和1个辅助列，方便矩阵进行彻底的压缩，使矩阵的规模逐步减小，运算量也大为减少；同时为了配合查找频繁 k-项集（k＞=2）的运算，设置了一个简单的辅助二维数组，用来记录下标组合情况。

定义1支持矩阵R：设A为任一给定的事务数据库，m为事务的个数，n为项目的个数，事务集Ti（i∈m），项目集 Ij（j∈n）。如果 Ij∈Ti（1≤i≤n，1≤j≤m），则支持矩阵rij=1，否则rij=0。为方便矩阵进行彻底地压缩，再为矩阵添加1列sum_r，记录每个事务的事务数，即累计每行的项数；为矩阵添加1行sum_c，记录每个项的项支持度；为矩阵添加一项，记录项的编码，则构造支持矩阵 R（m+2）×（n+1）。 支持矩阵 R如图 1所示。

图1 支持矩阵R

其中：第一行为记录项的编码；最后一行为每个项的支持度；第一列为每个事务的事务数；rij=1|0，（1≤i≤n，1≤j≤m）。

定义3 k-项集支持度：对支持矩阵R中的任意k列向量（除去第一列）进行对位（同行的元素）“与”运算，运算结果中“1”的个数称为k列向量的k-项集支持度。

根据 k-项集支持度的定义，结合 Apriori性质，可以得到以下性质。

性质 1 Xk是 k-项集，如果频繁（k-1）-项集 Lk-1中包含Xk的（k-1）-子项集的个数小于k，则Xk不可能是k维最大频繁项集。证明见参考文献[6]。

性质 2 设 k为 k-项频繁项集，若 T⊆I，且支持矩阵 R（m+2）×（n+1）中 T的事务数等于 k，由于 k-项集对于生成频繁（k+1）-项集没有作用，则求（k+1）-项集支持度时，该行事务T可删除。

性质 3 对于频繁 k-项集的集合 Lk，如果|Lk|＜k+1，则被挖掘的事务数据库最大频繁项集的次数为k。其中|Lk|是指 Lk的频繁 k-项集的个数。

证明：对于频繁（k+1）-项集 Ix={I1，I2，…，Ik+1}，一定有k+1个频繁k-项子集，若频繁k-项集的集合Lk元素个数小于k+1，则被挖掘的事务数据库不存在频繁（k+1）-项集。利用该性质可以提前终止搜索频繁集的循环。

2 多核并行编程技术

OpenMP是共享存储系统编程的工业标准，它具有简单、移植性好和可扩展等优点。OpenMP规范了一系列的编译制导、运行时库函数和环境变量来说明共享存储结构的并行机制。OpenMP实现的是线程级的并行，线程间通过读/写共享变量实现，使用Fork-Join的并行执行模式。

TBB是针对多核平台开发的一组开源的C++的模板库，基于GPLv2开源证书，支持可伸缩的并行编程[7-8]。TBB的编程模式通过使用模板来提供常见的并行迭代模式，使程序员即使在不具备很专业的同步、负载平衡、缓存优化等专门知识的情况下，也能够实现自动调度的并行程序，使得CPU的多个核心处于高效运转之中。TBB完全支持嵌套的并行，程序员可以很容易地创建自己的并行组件，进而构建大型的并行程序。TBB并行编程指定的是任务，而不是线程[9]，并以高效的方式将任务自动映射到线程，程序容易实现，且具有更优的可移植性和可扩展性。

3 关联规则挖掘算法的多核并行优化

本文在改进算法的同时，运用多核平台并行编程的优势，配合采用OpenMP的工作分区sections和并行库TBB的tbb_parallel_for，可以实现每个工作段都由多个执行核并行执行和负载均衡的并行执行固定数目独立循环迭代体，用于提高查找频繁项集的效率。基本流程如图2所示。

（1）并行扫描数据库 D，建立支持矩阵 R（m+2）×（n+1）。 TBB先初始化对象，再对包含m个事务n个项目的事务数据 库 D={T1，T2，… ，Tm}，项 目 集 I={I1，I2，… ，Im}，运 用OpenMP的工作分区sections并行优化扫描事务数据库D，建立支持 矩阵 R（m+2）×（n+1）。

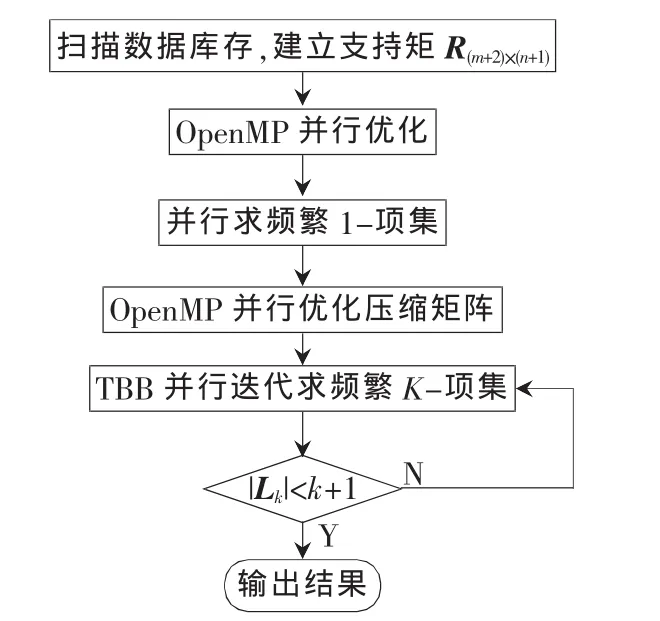
图2 并行优化流程图

（2）并行求频繁1-项集。k=1，计算最小事务支持度min_supsh=ceiling（min_sup×m），压缩矩阵的列，余下的项都是频繁1-项集。重新计算矩阵的sum_r列和sum_c行。

（3）k=2。

（4）并行压缩支持矩阵。按照性质1，先统计每个项目I1在频繁（k-1）-项集中出现的次数 bi，若 bi小于（k-1），则删除R中Ii对应的矩阵列。重新计算矩阵的sum_r列和sum_c行，按照性质2，删除不合条件的列和行，直到不能再压缩为止。

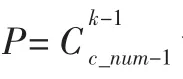
//R支持矩阵 Wp×k存放 P个 k维项组合对

4 实验及分析

为了验证基于多核并行技术的改进挖掘关联规则算法的性能，本文在Intel（R）Pentium（R）D CPU 3.0 GHz、1.86 GHz、1 GB内存的双核处理器系统上测试了参考文献[8]的BBM算法，改进的挖掘关联规则串行算法（以下称本文串行算法）及改进的挖掘关联规则的多核并行优化算法（以下简称多核并行算法）。从参考文献[10]选择数据集进行实验，事务数据库共100 000条事务，事务的平均长度为 12。实验测试结果见表 1，其中，加速比=本文串行执行时间/多核并行执行时间，CPU运行效率=加速比/核数。

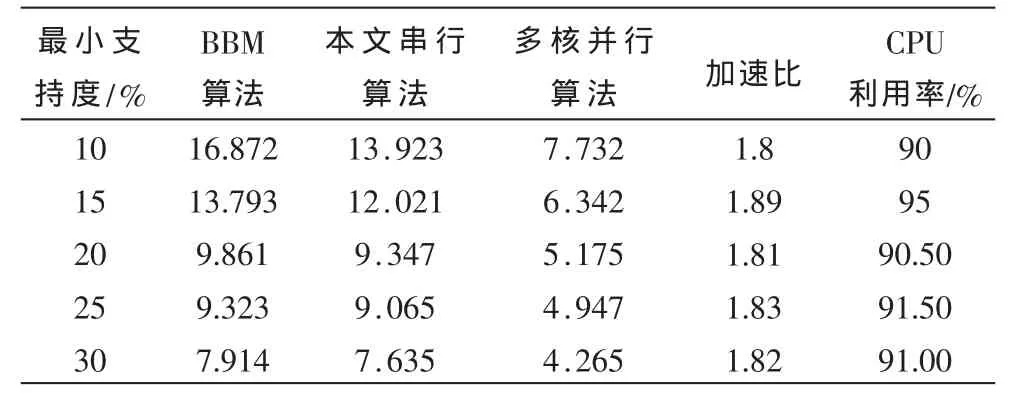
表1 三种算法执行时间比较

表1表明，支持度较高时，这三种算法的执行时间差别并不大；但当支持度逐渐降低时，与BBM算法相比，本文串行算法的执行时间要更短，而多核并行算法的执行时间几乎是本文串行算法的一半，具有高的并行挖掘效率。从加速比和CPU利用率分析，多核并行算法的多核CPU运行效率达到90%左右，充分调度了两个处理核心的资源，体现了计算机双核的优势。

关联规则技术是数据挖掘中的一种重要的基础算法，本文在深入研究Apriori算法的基础上，提出了一种改进的关联规则挖掘的多核并行优化算法，综合了布尔矩阵和多核并行编程的优点，节约了存储空间，减少了执行时间，具有较高的并行挖掘效率和多核CPU的利用率。本算法的设计方法对于相关算法的研究有较好的借鉴作用。

[1]何军，刘红岩，杜小勇.挖掘多关系关联规则[J].软件学报，2007，18（11）.

[2]Boeyen SX.509（2000）：4thEdition Overview of PKI&PMI Frameworks.http：//www.entrust.com.

[3]何中胜.基于向量的并行关联规则挖掘算法[J].计算机系统应用，2009，18（3）：42-45.

[4]曾万聘，周绪波，戴勃，等.关联规则挖掘的矩阵算法[J].计算机工程，2006，32（2）：45-47.

[5]张月琴.基于0-1矩阵的频繁项集挖掘算法研究[J].计算机工程与设计，2009，30（20）.

[6]张素兰.一种基于事务压缩的关联规则优化算法[J].计算机工程与设计，2006，27（18）：3450-3453.

[7]Reinders J.Intel threading building blocks[M].[s.l.]：O’REILLY 出版社，2007.

[8]胡斌，袁道华.TBB多核编程及其混合编程模型的研究[J].计算机技术与发展，2009，19（2）：89-101.

[9]Intel threading building blocks基于任务编程 [OL].http：//www.cppprog.com/2009/0401/96_2.html.

[10]ALMADEN I.Quest synthetic data generation code.http：//www.almaden.ibm.com/cs/quest/syndata.html.

Matrix compression based on multi-core TBB parallel algorithms for mining association rules

Wu Huaping，Zheng Xiaowei，Zhang Jianqiang

（College of Computer and Information Technology，Liaoning Normal University，Dalian 116081，China）

This paper analyzes the parallel algorithm for mining association rules exist，the paper proposes an improved multicore parallel association rule mining algorithm.The algorithm transforms the compression matrix of Apriori algorithm，and uses OpenMP and TBB technology under multi-core platform to complish cycle of serial procedures and task allocation in parallel of parallel design，to maximize the parallel association rule mining.

association rules；Apriori algorithm；frequent itemsets matrix；OpenMP；TBB；multi-core parallel

TP311

A

1674-7720（2011）01-0004-03

国家自然科学基金项目（No.60603047）

2010-09-05）

吴华平，男，1984年生，硕士研究生，主要研究方向：并行计算，多核计算机系统。

郑晓薇，女，1957年生，教授，主要研究方向：并行计算，多核计算机系统。

张建强，男，1981年生，硕士研究生，主要研究方向：并行计算，多核计算机系统。