地面探测雷达目标干扰问题的研究

叶春令

（国营8450厂，福建 三明 365001）

地面探测雷达目标干扰问题的研究

叶春令

（国营8450厂，福建 三明 365001）

讨论了主目标距离与干扰目标截面积之间的关系，结合工程实际应用，建立了干扰目标与主目标截面积比值，即主目标距离的数学模型。解决了主目标在不同距离时干扰程度的问题，并进行了仿真实验与结果分析。

地面探测雷达；CFAR；遮挡；干扰模型

噪声与杂波是雷达工作的固有环境，地面探测雷达要求在复杂的杂波与噪声背景下，保持恒定的虚警概率完成对动目标的自动检测，现代动目标检测（MTD）雷达大部分都采用参考单元（距离维）、恒虚警率（CFAR）处理技术来实现[1-2]。在大多数的应用场合下，由于CFAR在参考单元滑窗统计噪声时不可避免地存在杂波边缘与多目标干扰，尤其是近距离目标干扰，从而导致CFAR性能严重下降，甚至主目标被“遮挡”。

目前已经有大量文献[3-4]对CFAR技术在多（大）目标干扰环境下的检测性能进行了分析，并且得出CFAR技术在多目标环境中检测性能变差的结论；也有文献[5]对当CFAR技术失效时的干扰程度进行了一定的研究，但该文献[5]涉及的是一种理想状态，是基于各参考单元干扰目标的回波幅度一致的基础上进行的讨论，没有考虑因距离不同而引起的干扰强度的差异，因此只适用于主目标处于较远距离时刻。

本文就CA-CFAR和最小选择（SO）CFAR两种经典处理方法，结合实际工程应用，对目标干扰模型进行了数学推导与建模。给出了在雷达探测范围内，主目标被“遮挡”时干扰目标有效反射面积与距离之间的函数关系式，并对该数学推导模型进行了仿真验证。

1 CFAR技术介绍

CFAR检测器的结构框图如图1所示。输入的数据通过相参积累（FIR或FFT）处理后，为了减少系统损失提高多目标的发现概率，通常对各频道号信号分别做CFAR处理，图1描述的就是某一频道号进行滤波的结构框图。为了防止主目标信号泄露，通常在主目标前后相邻参考单元不参与噪声估计，图中Z1与Z2分别为主目标的前后m个单元的杂波噪声平均值，函数f（Z1、Z2）是对Z1、Z2进行进一步处理（求平均或选大或选小等），完成杂波噪声估值。

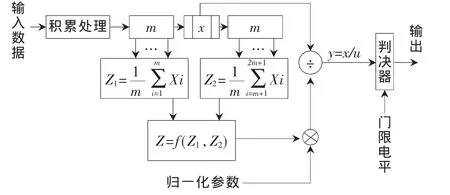
图1 CFAR结构框图

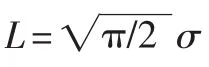
利用σ值对杂波估值进行归一化处理，主目标信号与归一化噪声的比值通过判决器，并根据给定的门限值完成目标的自动检测。

2 干扰目标δg-距离数学模型的建立

自由空间环境中，假设目标在距离R时雷达接收回波的信号功率为 Pr，则信号与杂波的功率可表示为P′r=Pr+X′，其中X′为杂波功率。单位时间内电磁波的行程S=Ct/2，其中C为光速，因此根据雷达方程得到：脉冲雷达第n个距离单元内目标信号的回波：

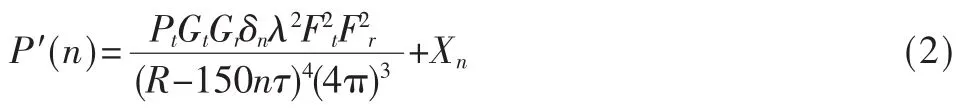
τ为距离单元延迟时间，单位 μs；n为自然数；Xn为第n个单元内的噪声功率。

通过CA-CFAR处理方法进行干扰目标强度模型推导，所有参考单元内信号回波功率估计：

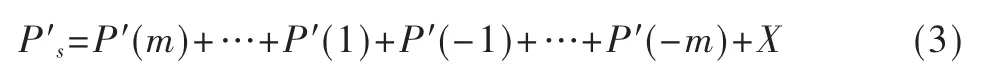
其中X表示2 m参考单元的噪声功率之和，P′（n）表示第n个单元内回波功率。

主目标没被“遮挡”而能被检测时所需满足的条件：

式（4）中，α为Rayleigh分布杂波的归一化参数，T为目标判决的门限电平。计算机按照式（4）进行自适应判决，当主目标的回波信号≥参考单元信号平均值与归一化门限的乘积时，认为有目标存在。

令D=PtGtGrλ2F2tF2r，对于同一部雷达参数 D都一致，回波大小在自由空间环境中主要与目标有效截面积（σ）和距离相关，由式（2）～式（4）整理后可得目标检测判决方程式：

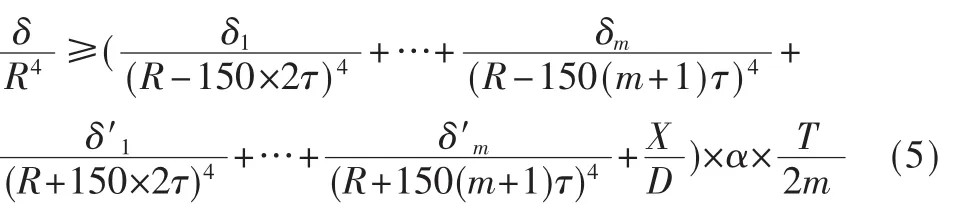
本文主要讨论主目标被其他大目标“遮挡”的问题，越靠近雷达的目标对主目标干扰程度越严重。所以主目标的前沿参考窗影响更为严重，而且参考单元中第一个参考单元的干扰目标影响最大，特别是在近距离处，雷达回波的信噪比很高，并且常常采用STC（灵敏度时间控制）来满足A/D采样动态以及收发机的动态要求，这样近距离噪声将非常小。因此为了简化计算以及便于仿真，故选择干扰最严重的情况进行讨论，即假设某相同频道号的干扰目标都集中在最靠近雷达的参考单元内，并且假设参考单元内的噪声与D比值为零，则式（5）可简化为：

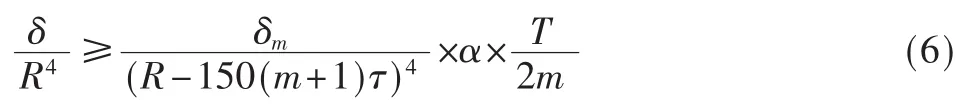
根据参考文献[5]，可知对于2m个独立同分布的参考单元，可获得满足恒虚警条件时雷达动目标的检测门限T如式（7）所示，其中Pfas为虚警概率。

在实际工程项目中，脉冲雷达一般都存在一定的近距离盲区，而且是与脉冲宽度成比例，其大小为 150×k×τ，其中 k为自然数，本文假设k＜m（地面探测雷达的近距离盲区要求都比较小）。可得到主目标不被“遮挡”的数学表达式：

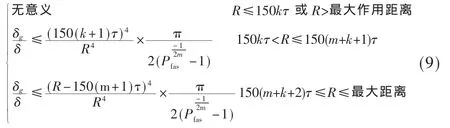
当信号处理机采用SO-CFAR处理方法时，主目标后沿参考窗口的信号估值更小，并且最靠近主目标的干扰目标影响最大，因此采用上述相同的推导方法可以得到单元平均选小SO-CFAR处理方法时，主目标不被“遮挡”应满足的数学表达式：

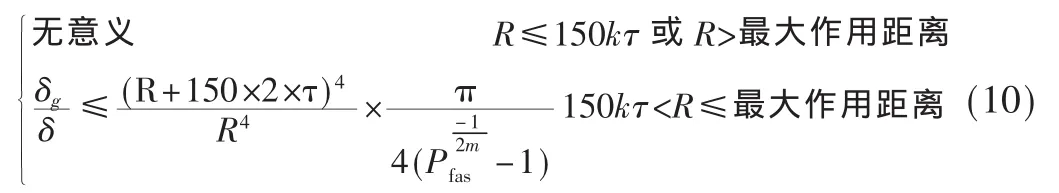
3 计算机仿真实验与分析

针对数学模型进行计算机仿真试验及分析，由于该数学模型是基于地面探测雷达工程实现过程推导，因此在仿真试验中对某些参数做如下假设：杂波和噪声的幅度为瑞利分布，雷达动目标检测的虚警概率Pfas=10-6，脉冲宽度为 0.2 μs，参考单元数 m依次取值为 8、16和 32三种参数，近距离盲区参数k取5。

图2所示为基于CA-CFAR处理方法的干扰模型，Δσ为干扰目标与主目标的截面积比值，R为主目标所处距离。当主目标在某一距离时，干扰目标比主目标至少大多少时可能“遮挡”主目标。图中目标的干扰情况在近距离表现得更为复杂，刚开始干扰目标要比主目标大很多（m=32时，Δσ大约为20 dB）才可能导致主目标被“遮挡”。随着距离的增加，两者截面积比值Δσ曲线也在不断下降，此时主目标变得很容易被“遮挡”（m=32时，Δσ最小将近-25 dB）。由于该距离段比较短，当距离达到150（m+k+1）τ时，干扰程度逐渐减弱，截面积比值 Δσ曲线快速上升。图中可以看出，在近距离干扰最严重的距离段，一个小目标就可能导致雷达“漏警”。

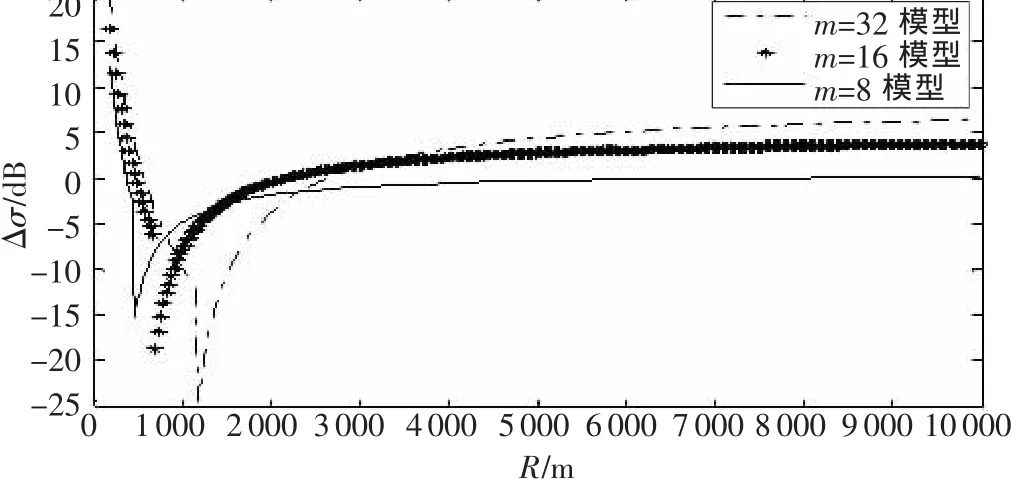
图2 CA-CFAR模型

图3所示为SO-CFAR处理模型时截面积比值Δσ与距离R的关系曲线图，从图中可以看出，随着距离增加，曲线呈下降趋势，到几公里后曲线趋于稳定，此时由于距离的差异而产生的的影响不大。

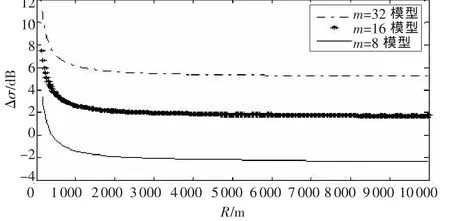
图3 SO-CFAR模型

由图2、图3可以看出SO-CFAR模型比CA-CFAR模型的抗干扰能力更强（特别是近距离），这也与众多的文献[7]研究结果相同。参考单元较多时，对于噪声功率估计更稳定，而且抗干扰能力较强，但是所涉及的距离越长越可能引入更多的干扰目标，同时参考单元越多所涉及的硬件开销越大。因此在工程应用中要综合考虑参考单元的数目。图2中也容易看出CA-CFAR处理方法，主目标在2 km以内很容易被干扰目标“遮挡”，由于式（2）中回波功率正比于目标有效截面积（Pr∝δ），因此可参考图2曲线，在原有的STC电路上，精心设计其控制曲线来降低近距离目标被干扰的可能性，提高目标的发现概率。

本文不仅从理论上，更侧重的是从工程实现的角度对问题进行建模、分析，结合 CA-CFAR与SO-CFAR处理技术，针对地面探测脉冲雷达进行研究，分析了目标距离与干扰目标之间的关系，并且进行仿真实验及结果分析，对从事雷达总体设计以及信号处理的研究起到一定的借鉴意义，也为雷达整机野外调试实验起到一些指导作用。

[1]刘敬兴.地面探测脉冲压缩雷达的动目标检测[J].电子技术应用，2010，36（1）：132-135.

[2]马晓岩，向家彬.雷达信号处理[M].长沙：湖南科学技术出版社，1998.

[3] MASHADEM B.M-sweepsdetection analysisofcellaveraging CFAR processors in multiple-target situations[J].IEE proc.-F，1994，141（2）：103-108.

[4]HUSSAINI E K，MASHADE M B.Performance of cellaveraging CFAR and order-statisticsdetectors processing correlated sweeps for multiple interfering targets[J].Signal Processing，1996，49（1）：111-118.

[5]杜朋飞，张祥军.单元平均恒虚警率检测中的一个新结论[J].现代雷达，2007，29（2）：60-62.

[6]郭仕剑，王宝顺.MATLAB7.X数字信号处理[M].北京：人民邮电出版社，2006.

[7]陈那.信号测试、处理与系统控制分析技术使用全书[M].北京：清华大学出版社，2005.

Study on the targets interfering problems of ground-based radar

Ye Chunling

（State-owned No.8450 Factory，Sanming 365001，China）

The connection between the distance of primary target and the cross-section of interference targets is discussed；to unite practical application of project，the mathematical model of cross-section ratio between interference targets and primary targetthe distance of primary target is established；the problem of degree of interference when primary target at different distance is resolved，and the experiment is simulated and the result is analysed.

ground-based radar；CFAR；mask；interference model

TN958.3

A

1674-7720（2011）01-0075-02

2010-06-10）

叶春令，男，1962年生，工程师，主要研究方向：地面雷达系统、光电结合系统总体分析与设计。