改进的遗传算法在神经网络结构优化中的应用

吴永明，吴 晟

（昆明理工大学 信息工程与自动化学院，云南 昆明 650051）

改进的遗传算法在神经网络结构优化中的应用

吴永明，吴 晟

（昆明理工大学 信息工程与自动化学院，云南 昆明 650051）

为了解决人工神经网络隐层节点数目难以确定的问题，针对三层BP神经网络提出了一种最大上限隐层节点数模型，并用改进的遗传算法对其优化。最后，将优化的神经网络对语音特征信号进行分类。仿真结果表明优化后的神经网络具有很好的泛化能力，验证了该方法的有效性。

遗传算法；神经网络；结构优化

人工神经网络[1]（ANN）和遗传算法[2]（GA）都是将生物学原理运用到智能计算研究中。人工神经网络是对人脑和动物神经的若干特点的人工模拟[3]，具有一个隐含层的神经网络就能逼近任意复杂的连续函数[4]。但在实际运用中，隐含层的节点数目、初始的权值或阈值的确定都依赖于使用者的经验[5-6]，隐含层的节点数太少，拟合的精度很难达到要求，反之，则可能出现过拟合现象，从而增加了训练的时间。遗传算法是从自然界生物的进化中得到启示，利用遗传算子进行全局搜索寻优。因此，利用遗传算法优化神经网络结构具有十分重要的意义。由于神经网络的初始化具有很大的随机性，输入和输出节点数一般根据具体问题而定，即便有确定的隐层节点数目，针对同一问题，得出的结论也可能不同。这是因为建立网络时，初始的权值或阈值都是系统随机分配的。近年来，许多研究者对神经网络的研究都是在随机性的基础上，这样就没有一个共同的初始权值和阈值的标准，参考文献[7]中提出用混合编码来优化神经网络结构，虽然同一起始权值或阈值条件得到了保证，但是对于高维输入的编码太长，不利于遗传优化计算。例如，输入、隐层、输出的节点数分别为 24、30、4，不加入阈值只对权值进行编码，编码的长度就达到了近千位。

为了统一起始权值和阈值标准，使节点数优劣的比较都局限在一个框架下，克服编码长度过长等问题，本文首先确定一个隐层节点数的上限，以隐层节点数上限建立一个初始网络，一旦网络初始化，网络节点数、权值、阈值被唯一确定在这个模型范围内，利用遗传算法在同一框架下优化后得到最优网络结构。

1 BP神经网络隐层节点的估计

在大量的BP应用实例中，对于三层的BP神经网络，输入和输出节点数目一般按照具体的情况而定，而隐层节点数目没有明确的理论依据[8]，大多数BP网络中隐层节点数的确定仍采用试凑的方式。根据Kolmogorov定理，最佳的隐层节点可以参考式（1）：

其中，l为隐层节点数，m为输入层节点数，n为输出层节点数，a为0～10之间的常数。在实际问题中，隐含层节点数的选择首先是参考公式来确定节点数的大概范围。为了使最佳隐层节点数落在模型的范围内，本文的思想是将这个范围适当扩大（即隐层节点数的上限）。在后面的仿真中，输入节点数为24，输出节点数为4，由式（1）得出l＜6+10=16。为了得出最好的测试效果，l取上限取值为30建立神经网络，然后用改进的遗传算法对其优化。

2 遗传算法优化BP神经网络的基本框架

遗传算法[9]是基于自然选择和生物进化的全局优化方法，通常由选择、交叉和变异三种基本操作组成。遗传算法优化BP神经网络的具体步骤如下：

（1）建立一个上限隐层节点数的BP神经网络，将网络的隐含层节点数用一个二进制字符串进行编码，用遗传算法求得最优隐层节点数目以及相应的节点在网络模型中的位置，提取相应的权值和阈值。

（2）将提取得到的最优节点数对应的权值和阈值建立BP神经网络，通过训练满足要求后得到最优的BP神经网络结构。遗传算法优化BP神经网络的算法流程如图1所示。

3 遗传算法的改进

3.1 编码与初始种群的产生

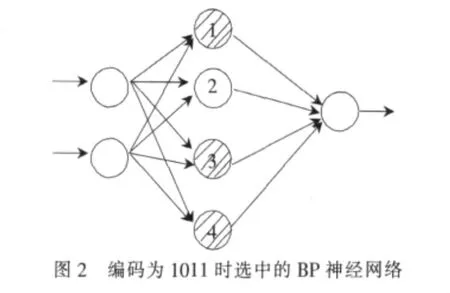
（1）编码。为了在确定的BP模型中找到最优的结构，本文采用二进制符号串d1d2…di…dn对神经网络的隐层节点编码，其中n为隐层节点数上限，di=1时表示该节点有效，di=0时表示该节点无效，如图2所示。设隐层上限节点数为4的BP网络，当编码为1011时，表明在网络中选择了第1、3、4个节点，即建立了含有隐层节点数目为3的BP神经网络，同时被选中的节点有关的权值或阈值有效。

（2）初始种群的产生。为避免随机方式产生初始个体在解空间上分布出现不均衡性，使搜索具有更高的全局性，本文采用式（2）产生初始种群：

其中，xi表示产生的第 i个个体中 1的个数，xL、xU分别表示个体中1的个数的下界和上界，m表示种群的大小，这样编码的好处在于：搜索过程中最优个体很容易被搜索到。

3.2 适应度函数

设种群的规模为m，即有m个个体，在遗传算法的每一代中，对每个个体译码提取相应的初始权值和阈值建立BP神经网络，输入N个样本对网络进行训练，设第 k个样本的实际输出和期望输出分别为：yk和 vk，k=1，2，3…N，均方误差 Ei的倒数作为适应度函数：

故个体函数的适应度fi可以定义为：

3.3 选择与交叉

进行选择操作时，按照适应度值的大小，采用轮盘赌算法进行选择，然后用父代中最优个体代替选择后的最差的个体，这样在每一代中都保留了上一代的最优个体，确保经过遗传运算得到的下一代最优个体的适用度不低于父代中最优个体的适用度，能避免进化过程中的振荡现象，同时也加快了搜索速度。交叉操作中，本文采用单点交叉方式，自适应动态交叉率，保留最优个体不进行交叉，并且回避适应度相近个体交叉。假设当代的平均适应度为favg，交叉的两个个体的适应度分别为ffirst、fsecond，设置交叉率的范围为 0.5～1，动态自适应交叉率采用式（5）：

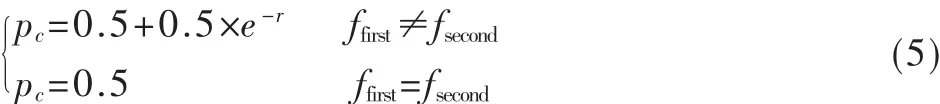
3.4 变异

在本算法中，为了使最优个体得到保护，将最优个体复制直接进入下一代。设总的遗传代数为M，连续出现N代没有产生新的最优个体，对变异率的改进如式（6）：

其中，a、b是很小的常数，可以根据具体情况调节 a、b的大小，N值越大，变异概率会增加，缩短了找到最优个体的时间。变异得到最优个体后，通过适应度函数计算出新的适应度值，对新的个体进行下一轮的选择、交叉和变异，直到找到最优解或者次优解。

4 实验仿真

本文将改进的遗传算法运用在语音信号特征分类中，并与没有经过优化的网络进行比较。本实验选取了民歌、古筝、摇滚和流行四种不同的音乐，每类音乐都用倒谱系数法提取500组24维语音特征信号，提取的语音特征信号如图3所示。

按第1节中隐层节点的估计，本实验隐层节点数的上限设置为 30，输入、输出节点数分别为 24和 4，遗传种群规模设为20，编码长度为30，遗传进化次数为100。每类语音信号有500组数据，样本总数为2 000，随机抽取1 500组数据用作网络训练，剩下的500组作为测试数据，对实验数据归一化后实验，遗传算法优化过程中最佳适应度以及平均适应度值的变化如图4所示。

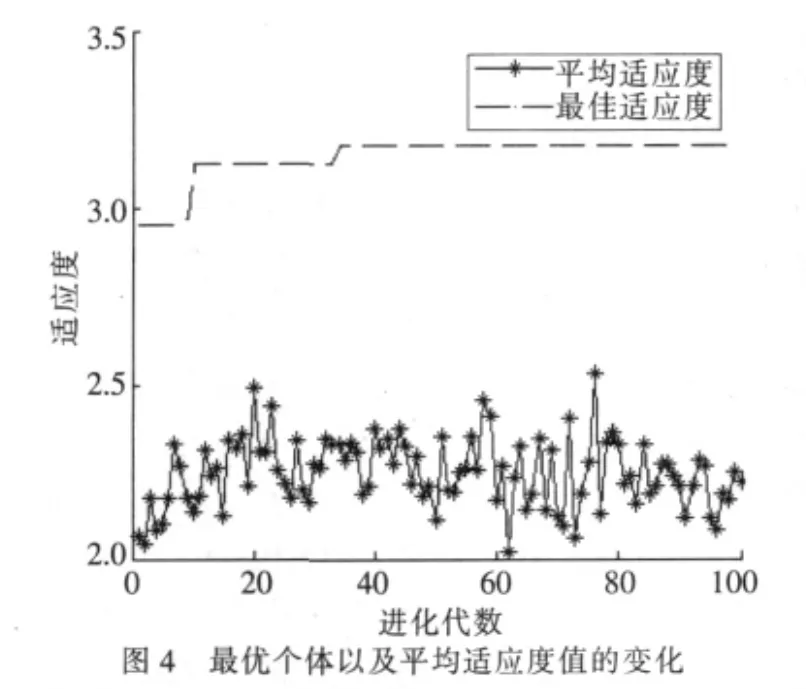
用改进的遗传算法对上限BP神经网络优化后，得到的最佳隐层节点数为12，经过训练后的BP神经网络对语音特征信号测试数据进行分类，先分别将民歌、古筝、摇滚、流行音乐编号为 1、2、3、4类，将预测的输出结果与期望分类编号比较（有负值的情况），得出分类误差如图5所示。

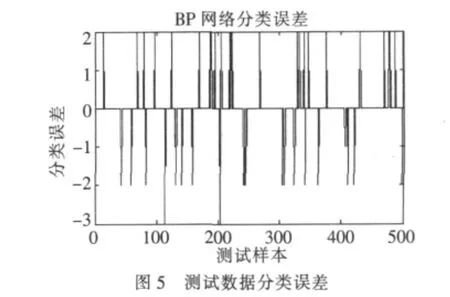
为了比较用遗传算法优化的神经网络与没有优化神经网络的性能，随机地从模型中选择隐层节点数为10、15、20、25、30 与节点数为 12 的 BP 神经网络的进行比较，初始的权值和阈值仍然来源于本实验中建立的上限隐层节点数BP神经网络，分类正确率如表1所示。

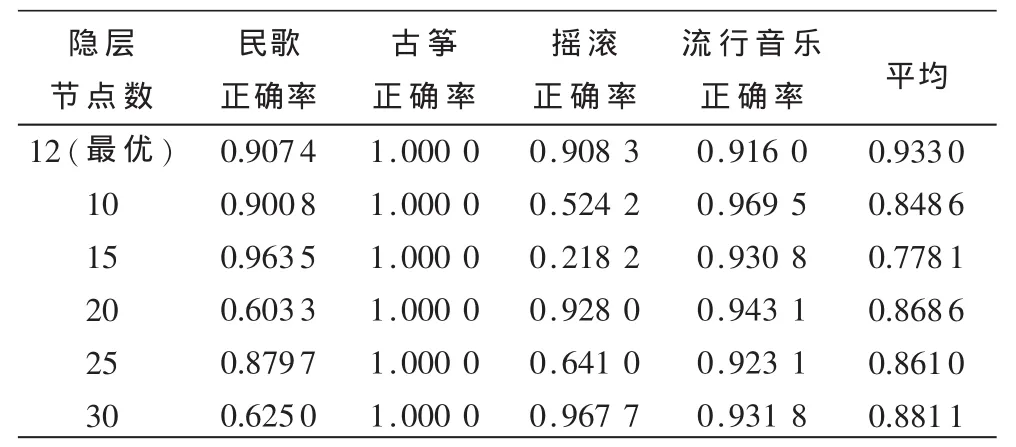
表1 不同隐层节点数正确识别率的比较

从表1的数据可以看出，在同一个上限隐层节点数的BP神经网络模型中，古筝的识别正确率都达到了100%，但优化后得出的隐层节点数目为12的BP神经网络的平均正确识别率高达93.3%，明显好于没有经过优化的网络，并且每一类的正确率比较均衡。

针对BP神经网络隐层节点数很难确定的问题，本文根据实际的问题建立了上限隐层节点数的BP神经网络，克服了每次建立BP神经网络分配权值和阈值的随机性，使评判的标准都统一在建立好的上限隐层节点数的BP网络模型范围内，并利用改进的遗传算法优化网络结构，最终找到网络结构的最优解或者次优解。该算法为选择隐层节点数提供了一种具有指导意义的方法，获得了更加合理的网络结构，运用到实际分类过程中也取得了较好的效果。

[1]TAKAHAMA S S.Structural learning of neural networks[J].IEEE International Conference on Systems. Man and Cybernetics.2004，12（1）：3507-3512.

[2]ZHOU Ming.Genetic algorithms：theory and application[M].Beijing：National Defence Industry Press，2001.

[3]ROVITHAKIS G A，CHALKIADAKIS I，ZERVAJIS M E.High-order neural network structure selection using genetic algorithms[J]. IEEE Transactions on Systems，Man and Cybernetics，2004，34（1）：150-158.

[4]HOMIK K M，STINCHCOMBE M. Multilayer feedforward networks are universal approximators[J].Neural Networks，1989，2（2）：359-366.

[5]KURKOVA V，KAINEN P C，KREINOVICH V.Estimates of the number of hidden units and variation with respect to halfspace[J].Neural Networks，1997，10（6）：1068-1078.

[6]MAIOROV V，MEIR R S.Approximation bounds for smooth functions in C（Rd）by neural and mixture networks[J].IEEE Transactions on Neural Networks，1998，9（5）：969-978.

[7]张伟栋，叶贞成，钱锋.基于混合编码的遗传算法在神经网络优化中的应用[J].华东理工大学学报，2008，34（1）：108-111.

[8]王建军，徐宗本.多元多项式函数的三层前向神经网络逼近方法[J].计算机学报，2009，32（12）：248-2488.

[9]范睿，李国斌，景韶光.基于实数编码遗传算法的混合神经网络算法[J].计算机仿真，2006，23（1）：161-164.

Application of structural optimization of artificial neural network based on improved genetic algorithm

Wu Yongming，Wu Sheng

（School of Information Engineering and Automation，Kunming University of Science and Technology，Kunming 650051，China）

It is difficult to determine the number of hidden layer of BP artificial neural network.In order to solve the problem，a maximum number of hidden nodes model is proposed in this paper for three layers BP neural network，and optimized by using improved genetic algorithm.Finally，The voice signature is classified by using optimized BP neural network.The results show the effectiveness of the algorithm.

genetic algorithm；neural network；structural optimization

TP305

A

1674-7720（2011）03-0079-03

2010-09-08）

吴永明，男，1982年生，硕士，主要研究方向：网络拥塞控制，人工智能。

吴晟，男，1960年生，教授，主要研究方向：人工智能，计算机网络，数据挖掘等。