底部钻具规则涡动轨迹的内摆线描述方法

马汝涛，纪友哲，贾 涛，韩 飞，朱英杰

(1.中国石油勘探开发研究院 研究生部，北京 100083;2.中国石油集团钻井工程技术研究院 机械所，北京 100195)

底部钻具规则涡动轨迹的内摆线描述方法

马汝涛1，纪友哲2，贾 涛2，韩 飞2，朱英杰2

(1.中国石油勘探开发研究院 研究生部，北京 100083;2.中国石油集团钻井工程技术研究院 机械所，北京 100195)

为了认识和控制钻井过程中的钻柱涡动，基于几何学原理提出内摆线描述方法。该方法将涡动视为规则运动，从分析钻柱外缘固定点的运动特性入手，求解底部钻具(BHA)与井壁的摩擦接触的运动轨迹方程，确定轨迹上各点的速度，分析钻柱自转和公转速度对底部钻具运动轨迹的影响。结果表明：底部钻具的涡动可能造成钻柱以远高于其自转速度的角速度沿着井壁快速公转，导致井下工具过早失效;钻柱规则涡动引起BHA外缘某点沿井壁的运动轨迹可用几何方法进行描述，轨迹方程证实线速度是影响井下工具磨损的重要参数;根据现场测试与室内试验所获得的钻柱规则运动轨迹可以反推涡动方程，从而掌握BHA的运动状态;利用内摆线描述法所得结果与文献试验数据吻合较好。

底部钻具;钻柱涡动;内摆线;运动轨迹;过程监测

底部钻具(BHA)的涡动现象普遍存在于钻井过程中［1-6］，可能引起钻铤偏磨、钻头磨蚀、随钻测量工具损坏等破坏性后果。为了认识BHA的涡动机制，须建立描述钻柱运动的合理方法。常见的方法有3类：基于机械振动原理建立BHA动力学模型，分析横向力对钻柱振动的影响规律［1，7-10］;通过室内试验测得特定结构BHA的运动参数，给出其轴线及外边缘的运动轨迹［3，11-12］;在钻井过程中采集钻压、转速、钩载等数据，根据运动学和动力学理论分析BHA涡动状态［2，13-15］。第 1类方法难以体现 BHA外缘与井壁的摩擦状况;第2类方法过程复杂且成本较高;第3类方法不能直观显示BHA运动状况。笔者将BHA涡动视为规则运动，引入内摆线方程直观、简洁地求解BHA外缘某一固定点的运动轨迹，通过分析轨迹特点了解钻柱涡动状况。

1 内摆线描述法基本方程

1.1 模型简化

考虑BHA与井壁发生接触的情况，如图1所示。图1中外圆为井壁，内圆为BHA截面的外壁。以井眼中心o为圆心建立平面直角坐标系oxy，ox轴与内圆交于点P，而P点同时也是内圆与外圆的接触点。将点P固定于内圆上，分析P点在oxy坐标系中的运动即可实现对钻铤的横向运动的描述。BHA的剖面可以选在任一位置，区别只是最终表达式相应的加入一项钻柱偏心量。

图1 BHA涡动示意图Fig.1 Sketch map of BHA whirling

1.2 几何内摆线方程

对于图1所示的几何模型，假定小圆沿大圆内侧做无滑动滚动，那么由小圆上一固定点P所形成的轨迹就称为内摆线，其参数方程为

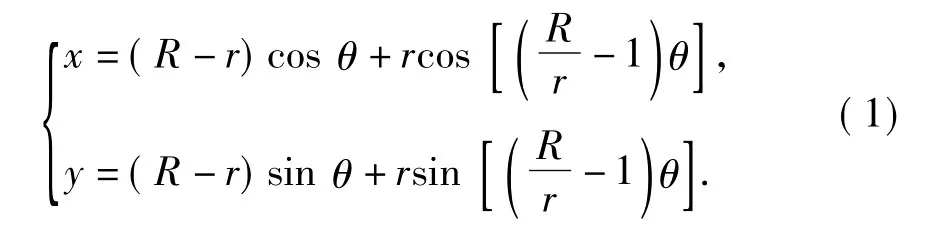
式中，R为外圆半径，m;r为内圆半径，m;θ为大圆中心o与小圆中心o'的连线沿逆时针方向摆动时与ox轴之间的夹角，rad。

若令R/r=k，则当k为整数时内摆线为封闭曲线，且曲线带有k个尖角;若k为有理数，令k=m/n为其最简形式，则内摆线具有m个尖角。

1.3 BHA涡动轨迹方程

BHA旋转过程中可能发生正向涡动(顺时针公转)或负向涡动(逆时针公转)，现以负向涡动为例求解固定点P的轨迹方程(图1)。为保证方程的合理性，假设：井壁为刚性，与BHA相互作用后不发生变形;井壁与BHA接触类型为点接触;BHA与井壁相对运动过程中始终保持相互接触。固定点P的参数方程为

式中，Ω为公转角速度，rad/s;ω为钻柱自转角速度，rad/s，自钻头上部向下看为顺时针方向，本文中取逆时针方向为正向，故ω前添加了负号;x和y分别为点P的横坐标和纵坐标。

对比分析方程(1)和方程(2)发现，如果令ω/Ω=R/r－1，则方程(2)即为标准内摆线方程。实际上，这种情况相当于钻铤沿井眼内壁做无滑动滚动，称为“负向纯滚动”。除去这种特殊情况，涡动都将伴随钻柱与井筒的相对滑动并磨损钻具。

若将ω和Ω作为变量处理，并考虑两者作用时间不一致，可引入参数t1和t2将方程(2)改写为

其中Rref=R－r－h(t)，h(t)是考虑到BHA可能脱离井壁的情况而引入的函数，其含义为BHA截面外缘到井壁的最短距离。实际应用中，可在钻铤的适当位置装入加速度计和位移计，测得BHA旋转和位移参数，代入方程(3)，即能描绘出合理的BHA运动轨迹图。

2 典型轨迹曲线

方程(2)是内摆线描述法的理论依据。根据方程特点可以判断当ω/Ω为某些特殊值时，P点轨迹应表现出与内摆线相似的性质。图2为R=120.65 mm，r=88.9 mm，ω=－12.56 rad/s时Ω取不同值对应的BHA外缘涡动轨迹。图2(a)中BHA只是围绕自身轴线旋转，旋转同时与井壁的一侧发生接触，此时的轨迹就是BHA的外缘轮廓。

图2(b)为Ω=ω时P点的运动轨迹，这种运动称为“正向同步涡动”，其特点是P点始终与井壁保持接触，沿井壁划出完整的圆形曲线。运动过程中，钻铤上除P点之外其他各点均未接触井壁。

图2(c)为Ω=ω/(R/r－1)=58.61 rad/s时P点的运动轨迹，此时Ω是ω的数倍，即钻柱以大大高于其自转速度的角速度沿着井壁快速公转。Johnson［11］通过试验认为，PDC钻头出现负向纯滚动的几率比正向涡动高许多;章扬烈［3］、Kesaven［5］等也在模拟试验中得出类似结论，说明这种运动状态较为常见。图2(c)的轨迹为标准内摆线，容易发现，函数在每个尖角处不可导，其物理意义表示尖角处P点线速度为0，而尖角之外的曲线上速度不为0，即在完成一条完整的内摆线时，BHA截面各点速度已经完成了多次周期性变化。BHA内应力的周期性变化势必对井下工具造成损伤。

图2 BHA外缘涡动轨迹Fig.2 Trajectories of BHA whirling

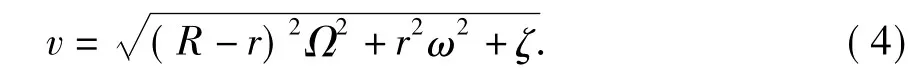
实际上，如果BHA发生了负向纯滚动，则不仅P点，其他所有与井壁接触的点的速度都可用式(4)计算。Shyu［16］也得到了与方程(5)相同的结果并将该速度作为关键参数分析了钻铤涡动对其磨损程度的影响。

其中

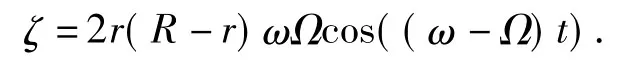
由ζ表达式可以发现，v为周期函数，其周期

3 内摆线描述方法的应用

Johnson［11］提出了一种提高PDC钻头横向稳定性的设计方法，为检验该方法的可靠性试制了多种专用钻头并进行室内试验。其中一种钻头用于校验涡动对钻进的影响，试验结果给出了一种典型的涡动轨迹(图3)。Johnson指出发生负向纯滚动时钻头切削齿外缘将生成瓣状切削痕迹，且瓣状曲线出现频率很高，但并未说明曲线的成因。

由图3可以看出，钻头滚动轨迹主要有如下特征：单一封闭曲线，自身没有交叉;具有15个波瓣;波瓣之间光滑连接。根据内摆线描述法可以作如下推理：曲线处于稳定状态，则公转与自转角速度之比Ω/ω为整数;波瓣数量说明井眼半径与钻头外径之比可以表示为R/r=15/n，其中n为与15互质的整数;波瓣中未出现尖角，严格来说并非达到无滑动的滚动效果，但考虑到实际试验条件对轨迹的影响，可以认为已经形成标准的内摆线。

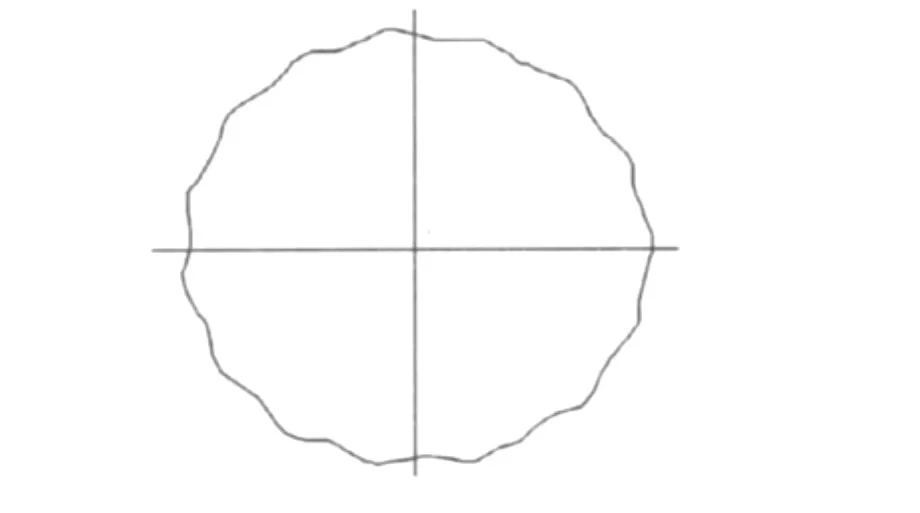
图3 典型的钻头负向纯滚动轨迹(由Jonhson原图修改)Fig.3 Typical locus of bit whirling(after Jonhson)

不妨验证一下给出的推理，令ω=－12.56 rad/s，则 Ω =rω/(R －r)=175.84 rad/s，而 Ω/ω =14 为整数，合乎推理。按上述参数绘制轨迹如图4所示，与图3有很大的相似性。

图4 推理得到标准内摆线Fig.4 Deduced hypocycloid curve

4 结论

(1)底部钻具的涡动可能造成钻柱以远高于其自转速度的角速度沿井壁快速公转，导致井下工具过早失效。

(2)钻柱规则涡动引起BHA外缘某点沿井壁的运动轨迹可以用几何方法进行描述，线速度是影响井下工具磨损的重要参数。

(3)根据现场测试与室内试验所获得的钻柱规则运动轨迹可以反推该点的涡动方程，从而掌握BHA的运动状态。

［1］JANSEN J D.Whirl and chaotic motion of stabilized drill collars［R］.SPE 20930，1992.

［2］REY-FABRET I，OUDIN N.Detecting whirling behaviour of the drill string from surface measurements［R］.SPE 38587，1997.

［3］ 章扬烈.钻柱运动学与动力学［M］.北京：石油工业出版社，2001：1-5.

［4］高德利，高宝奎.水平井段管柱屈曲与摩阻分析［J］.石油大学学报：自然科学版，2000，24(2)：1-3.

GAO De-li，GAO Bao-kui.Buckling and fractional analysis of drill string in horizontal well［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，2000，24(2)：1-3.

［5］KESHAVAN B.Jarring dynamics of drillstrings［D］.Cambridge：Massachusetts Institute of Technology，1993.

［6］ VANDLVER J K，NLCHOLSON W J，SHYU R-J.Case studies of the bending vibration and whirling motion of drill collars［R］.SPE 18452，1990.

［7］ MANSURE A J，FINGER J T，KNDSEN S D.Interpretation of diagnostics-while-drilling data［R］.SPE 84244，2003.

［8］HEISIG G，NEUBERT M.Lateral drillstring vibrations in extended-reach wells［R］.IADC/SPE 59235，2000.

［9］WU S X，PAEZ L，PARTIN U.Decoupling stick-slip and whirl to achieve breakthrough in drilling performance［R］.IADC/SPE 128767，2010.

［10］DUPRIEST E F，SOWERS F S.Maintaining steerability while extending gauge length to manage whirl［R］.SPE/IADC 119625，2009.

［11］JOHNSON S.A new method of producing laterally stable PDC drill bits［R］.SPE 98986，2006.

［12］ LANGEVELD C J.PDC bit dynamics［R］.SPE/IADC 23867，1992.

［13］MASON J S，SPRAWLS M.Addressing BHA whirl-the culprit in mobile bay［R］.IADC/SPE 35034，1996.

［14］MENAND S，SELLAMI H，SIMON C.How drillstring rotation affects critical buckling load? ［R］.IADC/SPE 112571，2008.

［15］NEUBERT M，HEISIG G，FORSTNER I.Verification of an advanced analysis model with downhole bending moment measurements［R］.SPE 93864，2005.

［16］SHYU R-J.Bending vibration of rotating drill strings［D］.Cambridge：Massachusetts Institute of Technology，1989.

Hypocycloid method for describing regular whirling of bottom hole assembly

MA Ru-tao1，JI You-zhe2，JIA Tao2，HAN Fei2，ZHU Ying-jie2
(1.Post Graduate School of Research Institute of Petroleum Exploration ＆ Development，PetroChina，Beijing 100083，China;2.Department of Drilling Machinery of Drilling Research Institute，CNPC，Beijing 100195，China)

On the basis of geometry，a hypocycloid method was proposed to identify and control drillstring whirling.Treating the whirling as a regular pattern，this method was used to describe motion characteristics of a fixed point on drillstring circumference，to solve equations representing bottom hole assembly(BHA)motion trajectories，to define velocities of each point on the trajectory，and to analyze the impacts of rotation and revolution speeds on BHA whirling.The results show that whirling might cause drillstring rolling around borehole wall with a revolution speed much higher than rotating，inducing downhole tools premature failures.The regular motion patterns of a fixed point on BHA circumference can be expressed by geometry measures，and the trajectory equation indicates that the linear velocity plays an important role in tool wear.The whirling equations representing BHA motion can be worked out from inversions of field and laboratory tests and the results properly match documented tests.

bottom hole assembly;drillstring whirling;hypocycloid;motion trajectories;process monitoring

TE 243

A

10.3969/j.issn.1673-5005.2011.03.015

1673-5005(2011)03-0076-03

2010－08－30

国家“863”高技术研究发展计划项目(2006AA06A107)

马汝涛(1982－)，男(汉族)，山东青岛人，博士研究生，从事套管钻井工作机制研究和井下工具研发工作。

(编辑 李志芬)