差分跳频与常规跳频抗部分频带干扰的性能比较

朱毅超

(中国舰船研究院，北京 100192)

差分跳频与常规跳频抗部分频带干扰的性能比较

朱毅超

(中国舰船研究院，北京 100192)

在差分跳频抗部分频带干扰比特误码率(BER)的理论分析结果基础上，将差分跳频系统与常规快跳频系统抗部分频带干扰的BER联合—切尔诺夫界进行了比较。在差分跳频采用维特比译码，且两系统均采用加权能量度量，并具有相同频谱效率的情况下，比较结果表明:在加性白高斯噪声(AWGN)与瑞利信道下，差分跳频的抗部分频带干扰性能明显优于快跳频系统。在AWGN信道下，当差分跳频的每跳传输比特数与快跳频系统的每符号比特数均为1，且BER大于10－6时，差分跳频系统达到相同BER所需的信干比(SJR)较快跳频系统低6 dB。

差分跳频;快跳频;部分频带干扰;切尔诺夫界

0 引言

差分跳频是近十年来所提出的一种新型跳频体制［1－2］。与常规跳频系统不同，由于差分跳频系统的发送频率不是通过伪随机码控制的，而是直接由信息数据经G函数变换确定，因此，差分跳频系统接收端无需进行复杂的伪随机码同步过程，从而实现了短波信道中的高速数据传输。

窄带人为干扰是制约常规跳频系统与差分跳频系统性能提高的重要因素之一。研究常规跳频与差分跳频的抗干扰性能，以及提高其抗干扰性能的方法，均是常规跳频与差分跳频领域的重要研究内容［3－6］。本文根据作者在该领域所得到的研究成果［3－5］，对传统快跳频与差分跳频抗部分频带干扰的性能进行全面、深入地比较与分析，并定量地给出差分跳频技术在抗部分频带干扰性能方面所具有的优势。

1 系统模型

差分跳频系统与快跳频系统如图1所示。

图1 差分跳频与快跳频系统框图Fig.1 Block diagrams of DFH system and FFH system

在图1(a)中，当前跳输入信息数据符号经G函数编码后，确定当前跳的发送频率号，MFSK调制器根据该频率号生成对应的频率并发送。在接收端，非相干能量检测器对所有可用频点上的能量进行检测，维特比译码器利用该能量检测结果对发送数据符号进行维特比译码。在图1(b)中，输入信息数据先进行重复编码，其编码输出经MFSK调制后，再进行伪随机码跳频，且每跳传输1个编码符号。在接收端，解跳后的信号先进行非相干能量检测，再对各编码符号的能量检测输出进行分集合并，最后根据合并结果对发送数据符号进行判决。

部分频带干扰可以模拟为加性高斯噪声。在差分跳频系统中，假设所有可用频率数为M，干扰机将总的噪声功率均匀地分布在Q(Q≤M)个跳频子频带内，于是在任一特定频率上存在干扰的概率为ρ=Q/M，而不存在干扰的概率为1－ρ。令NJ为差分跳频总带宽内的平均干扰单边功率谱密度，则在存在干扰的子频带内，干扰单边功率谱密度为NJ/ρ。在常规跳频系统中，令ρ表示干扰带宽与系统总带宽之比，并且假设每个跳频子频带要么整体位于干扰频带内，要么整体位于干扰频带外。同时，若考虑信道中存在衰落，则将其建模为频率非选择性瑞利慢衰落信道，此时各跳信号的幅度服从相互独立的瑞利分布，且各跳信号间不存在符号间干扰。

2 两系统抗部分频带干扰的性能

对差分跳频与快跳频的抗部分频带干扰性能比较将基于两系统在部分频带干扰下的比特误码率(BER)联合－切尔诺夫界。在比较中，假设2种系统均具有相同的信息比特传输速率。然而，由于常规跳频系统采用伪随机码确定跳频图案，而差分跳频系统采用输入信息与G函数确定跳频图案，二者的跳频机制不同，因此，在信息比特传输速率相同的前提下，2种系统可能具有不同的跳频总带宽。为了合理地进行比较，假设2种系统跳频总带宽内的平均干扰单边功率谱密度NJ相同，同时，还假设背景热噪声不存在，且2种系统均具有精确的干扰状态信息，从而可以采用加权能量度量。

差分跳频维特比译码的性能与其G函数网格图的最小自由距离dfree紧密相关。在维特比译码过程中，由于译码算法将发送频率序列作为一个整体进行最大似然序列译码，其BER性能由dfree跳的接收信号联合确定，因此，可以认为它具有分集合并的效果。对于传统快跳频系统，每个信息符号在多跳中传输，每跳的干扰状态相互独立，在接收端对多跳信号进行合并接收，则其也可视为采用了分集技术。显然，将采用序列译码的差分跳频系统与快跳频系统进行比较是合理的。为了设定比较的参数，本文根据文献［7］中所提出的“频谱效率”的概念，定义差分跳频系统的频谱效率为信息比特传输速率与系统总带宽的比，定义快跳频系统的频谱效率为信息比特传输速率与解跳后带宽的比，且在比较中假定两系统具有相同的频谱效率，则

式中:bD为差分跳频系统的每跳传输比特数;bF为快跳频系统每符号比特数;d为快跳频系统每符号所传输的跳数，即快跳频系统的分集重数。

利用式(1)便可确定两系统性能比较中所用的各种参数。

下面给出两系统在部分频带干扰下的BER联合－切尔诺夫界。对于差分跳频系统，文献［5］给出了在莱斯衰落信道下，采用加权能量度量的抗部分频带干扰BER联合－切尔诺夫界。由于在莱斯信道下信号幅度由直通分量和散射分量组成，当散射分量为0时，信道转化为无衰落的AWGN信道，而当直通分量为0时，信道转化为瑞利衰落信道，因此，AWGN信道与瑞利衰落信道均可视为莱斯信道的特殊情况。差分跳频系统在AWGN与瑞利信道下抗部分频带干扰的BER联合－切尔诺夫界，可由其在莱斯信道下的BER联合－切尔诺夫界得到。

差分跳频系统抗部分频带干扰的BER联合－切尔诺夫界可表示为

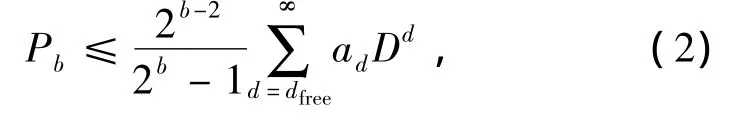
式中:Pb为比特误码率;dfree为G函数网格图的最小自由距离;ad为G函数网格图中所有长度为d的错误路径所对应的输入符号错误数;b为系统每跳传输比特数，切尔诺夫参数

在莱斯衰落信道及部分频带干扰下，采用加权能量度量的差分跳频系统，其切尔诺夫参数D的表达式为［5］

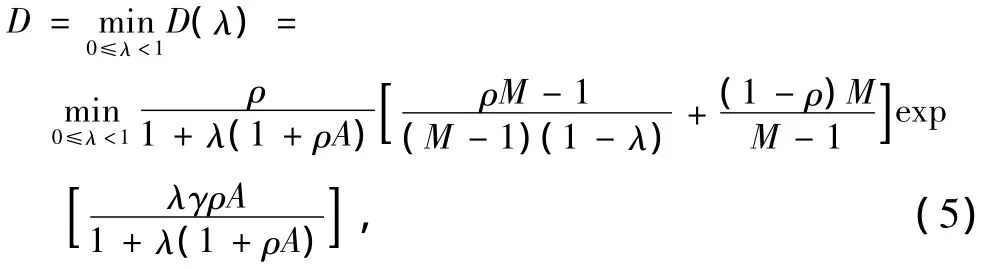
通常，使D最小的λ值可通过将D(λ)的表达式对λ求导并令其为0，从中解出λ而得到。但在莱斯信道下，式(5)中的D(λ)对λ求导将得到1个三次方程，而无法求解出λ的闭合表达式，此时，λ的值只能通过计算机搜索得到。

如前所述，AWGN信道相当于莱斯信道中散射分量为0时的特殊情况，因此，在式(5)中令γ趋于无穷大，则 A的值趋于0，而 γA的值趋于bb/NJ。于是在AWGN信道下，D(λ)的表达式化为

式中，Eb为比特能量。

同样地，该式对λ求导仍将得到一个三次方程，因此只能通过计算机搜索确定λ的值。

由于瑞利信道是莱斯信道中直通分量为0时的特殊情况，因此，在式(5)中令γ=0，则A的值变为b E—b/NJ。于是在瑞利信道下，D(λ)的表达式化为

当ρ≠1/M或1时，将式(7)对λ求导并令其为0，可得方程

该方程是1个一元二次方程，可以从中解出，

对接收机而言，若将D视为ρ的函数，则可对ρ的M个可能的取值，确定D的最大值，

将Dwc代入式(2)中，便可得到接收机的最坏情况BER上界。

对于快跳频系统，在AWGN信道及部分频带干扰下，其BER的联合切尔诺夫界为［6］

式中:b为每符号比特数，它等价于差分跳频系统的每跳传输比特数;d为快跳频的分集重数，它等价于差分跳频系统G函数网格图的最小自由距离，且

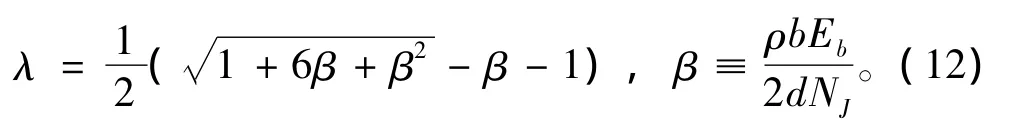
对于0＜ρ≤1，均有1个最坏情况干扰因子ρwc，使得 BER 达到最大值 Pb，wc。当bEb/dNJ≥3 时，

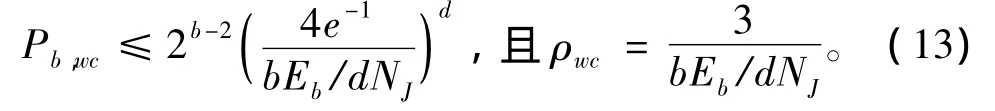
当 bEb/dNJ≤ 3，Pb，wc仍由式(11)及式(12)给出，且 ρwc=1。

在瑞利衰落信道下，其BER的联合切尔诺夫界为［6］

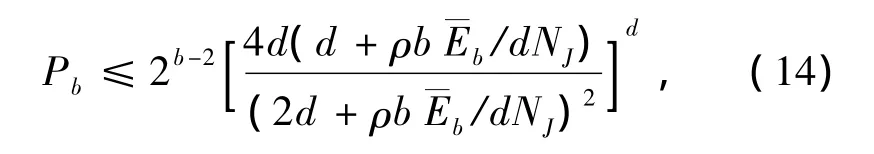
此时，最坏情况干扰因子ρwc=1。

3 性能比较

当差分跳频系统的每跳传输比特数bD与快跳频系统的每符号比特数bF均为1时，在AWGN信道下，对于不同的差分跳频系统可用频率数M，以及快跳频系统分集重数d，差分跳频系统与快跳频系统抗最坏情况部分频带干扰的性能比较如图2所示。

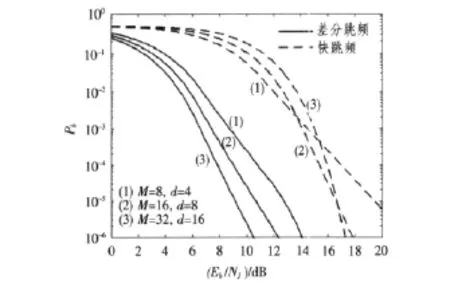
图2 AWGN信道下，bD=bF时，差分跳频与快跳频的Pb与Eb/NJ关系曲线Fig.2 BER upperbounds of DFH and FFH under AWGN channels for bD=bF

图2中，M与d的关系由式(1)确定。从图中可见:差分跳频系统的性能明显优于快跳频系统，当BER＞10－6时，差分跳频系统达到相同BER所需的信干比(SJR)比快跳频系统约低6 dB。

当差分跳频系统的可用频率数M等于快跳频系统MFSK调制的总频率数2bF时，在AWGN信道下，对不同的M，差分跳频系统与快跳频系统抗最坏情况部分频带干扰的性能比较如图3所示。

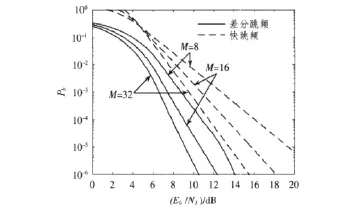
图3 AWGN信道下，M=2bF时，差分跳频与快跳频的Pb与Eb/NJ关系曲线Fig.3 BER upperbounds of DFH and FFH under AWGN channels for M=2bF

图3中，假设差分跳频系统每跳传输比特数bD仍为1，则由式(1)，d=bF=log2M。从图中可见:在这种情况下，差分跳频系统的性能仍优于快跳频系统。当BER＞10－3时，差分跳频系统达到相同BER所需的SJR比快跳频系统约低4 dB;而当BER＜10－3时，差分跳频系统达到相同BER所需的SJR比快跳频系统约低6 dB。

当差分跳频系统的每跳传输比特数bD与快跳频系统的每符号比特数bF均为1时，在瑞利信道下，对不同的差分跳频系统可用频率数M，以及快跳频系统分集重数d，差分跳频系统与快跳频系统抗最坏情况部分频带干扰的性能比较如图4所示。

图4 瑞利信道下，bD=bF时，差分跳频与快跳频的 Pb 与b/NJ 关系曲线Fig.4 BER upperbounds of DFH and FFH under Rayleigh fading channels for bD=bF

图4中，M与d的关系仍由式(1)确定。从图中可见:与AWGN信道下的情况不同，在瑞利信道下，当BER＞10－8时，差分跳频系统的性能优于快跳频系统;而当BER＜10－8时，快跳频系统的性能优于差分跳频系统。然而，在差分跳频系统性能占优势的BER范围内，其优势依然明显，例如，当BER=10－4时，差分跳频系统达到相同BER所需的SJR比快跳频系统仍约低6 dB。

当差分跳频系统的可用频率数M等于快跳频系统MFSK调制的总频率数2bF时，在瑞利信道下，对不同的M，差分跳频系统与快跳频系统抗最坏情况部分频带干扰的性能比较如图5所示。

图5中，假设差分跳频系统每跳传输比特数bD仍为1，由式(1)，d=bF=log2M。从图中可见:此时与AWGN信道下的情况相同，差分跳频系统的性能仍优于快跳频系统。当BER＞10－6时，差分跳频系统达到相同BER所需的SJR比快跳频系统约低3 dB。

图5 瑞利信道下，M=2bF时，差分跳频与快跳频的 Pb与b/NJ关系曲线Fig.5 BER upperbounds of DFH and FFH under Rayleigh fading channels for M=2bF

4 结语

基于差分跳频抗部分频带干扰BER的理论分析结果，将差分跳频系统的抗干扰性能与传统快跳频系统抗部分频带干扰的联合－切尔诺夫界进行了比较。比较结果表明:1)在AWGN与瑞利信道下，差分跳频系统的抗部分干扰性能明显优于快跳频系统;2)在AWGN信道下，当差分跳频的每跳传输比特数与快跳频系统的每符号比特数均为1，且BER＞10－6时，差分跳频系统达到相同BER所需的SJR比快跳频系统约低6 dB。

［1］HERRICK D L，LEE P K.CHESS a new reliable high speed HF radio［A］.MILCOM'96 Conference Proceedings［C］.Washington，DC:IEEE，1996:684 －690.

［2］HERRICK D L，LEE P K，LEDLOW L L，Jr.Correlated frequency hopping-an improved approach to HF spread spectrum［A］.1996 Tactical Communication Conference Proceedings［C］.Fort Wayne，IN，IEEE，1996:319 －324.

［3］朱毅超，甘良才，熊俊俏，等.短波差分跳频系统抗部分频带干扰性能分析［J］.电波科学学报，2006，21(6):885－891.

［4］朱毅超，甘良才，郭见兵，等.卷积码差分跳频系统抗部分频带干扰的性能［J］.通信学报，2009，30(12):85 －92.

［5］ZHU Y C，GAN L C，LIN J，XIONG J Q.Performance of differential frequency hopping systems in a fading channel with partial-band noise jamming［C］.WiCOM 2006，2006:1－4.

［6］SIMON M K，OMURA J K，SCHOLTZ R A，et al.Spread spectrum communications handbook［M］.北京:人民邮电出版社，2002.

［7］MILLS D G，EGNOR D E，EDELSON G S.A performance comparison of differential frequency hopping and fast frequencyhopping［A］.MILCOM 2004 Conference Proceedings［C］.Monterey，CA，IEEE，2004:445－450.

Performance comparison of differential frequency hopping and conventional frequency hopping against partial-band jamming

ZHU Yi-chao
(China Ship Research and Development Academy，Beijing 100192，China)

Based on the theoretical bit error rate(BER)results of differential frequency hopping(DFH)against partial-band jamming，this paper compares the union-chernoff BER bounds of DFH and conventional fast frequency hopping(FFH)against partial-band jamming.In comparison，Viterbi algorithm is used by DFH and weighted energy metric is used by both DFH and FFH.Furthermore，equal spectrum efficiency is assumed for both systems.Comparison results show that DFH has significantly better antijamming performance compared with FFH.If DFH transmits 1 bit per hop，FFH transmits 1 bit per symbol，and BER is larger than 10－6，DFH requires 6 dB less signal-to-jamming ratio(SJR)than FFH to achieve the same BER.

differential frequency hopping;fast frequency hopping;partial-band jamming;chernoff bounds

TN914.41

A

1672－7649(2011)06－0061－05

10.3404/j.issn.1672－7649.2011.06.015

2011－05－06

国家自然科学基金资助项目(60832006)

朱毅超(1980－)，男，博士，工程师，主要从事抗干扰通信理论与技术的研究。