基于粒子群优化的多路径规划方法研究

王 丹

(中国舰船研究院，北京 100192)

基于粒子群优化的多路径规划方法研究

王 丹

(中国舰船研究院，北京 100192)

借鉴遗传算法求解多峰函数优化问题的思想，开展了基于粒子群优化的多路径规划方法研究。给出了多路径规划算法的基本思想和算法流程，讨论了算法中粒子群的多样化方法以及多种群的隔离进化策略，并针对多个仿真环境进行了仿真实验。仿真结果表明，本文设计的多路径规划算法能针对不同的环境模型进行环境划分，正确、有效地规划出多条运动路径。

粒子群优化;多路径规划;多种群进化

0 引言

全局路径规划是船舶智能化航行的关键技术之一，其主要任务是在对环境已知的情况下，使船舶避开环境中的障碍物，按照某一最优指标安全到达预定的位置［1－2］。在通常的路径规划算法中，对规划路径优劣的评价完全是依靠适应值评价函数来进行的，算法求得的最优路径的性能与评价函数密切相关。但在实际使用过程中，由于路径规划问题本身的复杂性、船舶运动的复杂性以及外部环境的复杂性，采用任何一个单一的评价函数都是不完善的，很难用一个统一的适应值评价函数把所有要考虑的重要因素都包括进去。而且，人的思维总有一定的片面性，不能兼顾到所有的限制因素。因此，本论文借鉴遗传算法求解多峰函数优化问题的思想［3－5］，在标准粒子群优化算法的基础上设计了多路径规划算法，并通过对多个不同环境的仿真实验，验证了算法的正确性和有效性。

1 多路径规划算法的基本思想

多路径规划的目的是同时寻找多个最优及次优可行路径，供决策者选择使用。也就是说，规划算法不仅要搜索到全局最优解，同时还要获得若干个次优解。由此看来，多路径规划问题也就是多峰函数优化问题。本文设计的多路径规划算法的思想是以标准粒子群算法为基本算法，借鉴并结合遗传算法多峰函数优化求解中的适应值共享技术和多种群进化策略，从而实现群体的多样性，同时获得若干最优和次优解。

2 多路径规划算法设计

多路径规划算法流程如图1所示。算法主要分为粒子群多样化和多群体隔离进化2个阶段，每个阶段的算法均在文献［6］给出的标准粒子群算法模型的基础上改进得到。

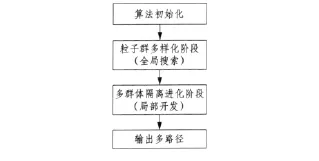
图1 多路径规划算法基本流程Fig.1 Basic flow chart of multi-path planning method

粒子群多样化阶段主要是进行全局搜索，通过在标准粒子群算法的基础上引入聚类分析和适应值共享等策略，从而确保粒子的充分多样化，产生大量符合不同特性的子群体;多群体隔离进化阶段主要是进行局部开发，通过在多个子群体间采用隔离进化策略，从而确保多路径的快速生成。

3 粒子群的多样化

粒子群的多样化阶段算法流程如图2所示。算法首先对所有粒子进行聚类分析，形成多个子群体;然后对各粒子进行适应值评价与共享，并采用标准粒子群算法进行位置、速度更新;当粒子位置更新后，得到子代粒子，在子代粒子和父代粒子中进行粒子选取。算法重复执行，直到满足多样化结束条件为止。

下面对粒子群多样化过程中的几个主要内容进行详细说明。

3.1 粒子聚类分析方法

粒子聚类分析的目的是要按照各粒子所代表路径的不同特点将整个粒子群划分为多个子群体，从而保证具有不同特性的各子群体均能被充分的多样化。该方法将各粒子所代表的路径之间是否存在障碍物作为聚类分析的判据。若2个粒子所代表的路径之间不存在障碍物，则这2个粒子属于同1个子群体;若2个粒子所代表的路径之间存在障碍物，则这2个粒子属于不同的子群体。这样，所有的粒子就按其所对应路径的空间分布被聚类为多个子群体。

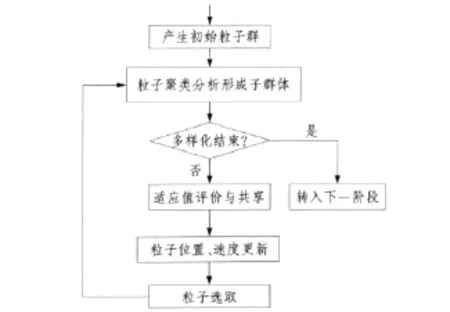
图2 粒子群多样化阶段算法流程Fig.2 Algorithm flow chart of particle swarm diversified moment

假设粒子群 C 表示为{c1，c2，…，cN}，其中，N 为粒子个数，ci(i=1，2，…，N)为粒子群中的任意粒子。粒子群聚类后形成的子群体表示为Z={Z1，Z2，…，ZpopNum}，其中，popNum 为聚类个数，Zi(i=1，2，…，popNum)代表聚类后的各子群体。则粒子群聚类分析的具体过程如下:

1)取第1个粒子c1，令其属于聚类Z1，即 c1∈Z1。

2)计算c2与Z1中任意粒子所代表的路径之间是否存在障碍物，若不存在障碍物，则c2∈Z1;否则，形成新聚类 Z2，即 c2∈Z2。

3)假设在2)中，粒子c1和c2分别属于不同的聚类Z1和Z2。取粒子c3，计算该粒子与Z1和Z2中任意粒子所代表的路径之间是否存在障碍物，若均存在障碍物，则形成新聚类Z3，即c3∈Z3;否则，粒子c3属于聚类Z1或Z2。

4)按上述过程判断剩余所有粒子。

重复上述过程，直至整个粒子群C中所有的粒子都已经被划分进相应的子种群为止。同时计算子种群的个数和每个子种群中所拥有个体路径的数量。

3.2 多样化结束条件

粒子群多样化的目的是为了确保生成的粒子能尽可能多的反映不同特性的路径。在上面的内容中我们已经知道，每个子群体代表一类具有相同特性的路径，因此，多样化结束的选取条件如下:

1)粒子群经聚类分析后得到的子群体稳定，且没有丢失。

2)每个子群体中的粒子数量要大于某一数值cNum(本文仿真实验中取为20)。

3.3 粒子更新策略

在标准粒子群优化算法中，每次粒子位置更新和速度更新后，父代粒子被直接转化为子代粒子。因此，算法寻优过程的每一迭代步中，粒子群的总数是不变的。而本文讨论的用于求解多路径规划问题的粒子群优化算法需要充分实现粒子群的多样化，子群体的数目是不定的，而且每个子群体中均要保证生成一定数量的粒子，因此，无法采用标准粒子群优化算法中的粒子更新策略。

在粒子群多样化阶段，粒子更新策略如下:

1)在每一迭代步粒子进行位置更新后，父代粒子要被保存，与子代粒子共同竞争，形成新的粒子。算法维持总的粒子数目取为1.5*popNum*cNum。其中，popNum为子群体个数，cNum为多样化结束时每个子群体需要达到的粒子数目。

2)在每一迭代步中，若父代粒子与子代粒子的总和大于算法所要维持的总粒子数，则按适应值大小从高到低选取适量粒子保存即可;若父代粒子与子代粒子的总和小于算法所要维持的总粒子数，则保存所有粒子，待下一迭代步中再做判断。

3.4 适应值评价与共享

适应值评价与共享首先采用适应值评价函数对各粒子所代表的路径进行优劣评估，得到各路径的适应值;然后采用适应值共享方式对各粒子适应值进行再处理，从而改善粒子群优化算法的全局搜索能力，保持粒子的多样性。本文算法采用的适应值评价函数FitBase(c)和适应值共享处理函数Fit(c)分别如式(1)和式(2)所示:

式中:S(c)为路径的安全性因素，用路径到障碍物的最短距离来评估;D(c)为路径的快速性因素，用路径的总长度来评估;M(c)为路径的适航性因素，用路径的平滑程度来评估;w1，w2，w3分别为各因素的权值;Ni为粒子c所属的第i个子群体中所含有的粒子数目;popNum为子群体的个数。

4 多群体的隔离进化

在粒子群多样化阶段结束后，算法进入多群体隔离进化阶段。多群体隔离进化阶段的算法流程如图3所示。

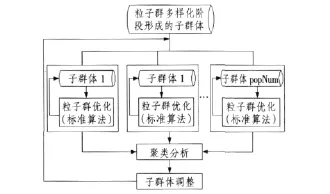
图3 多群体隔离进化阶段算法流程Fig.3 Algorithm flow chart of evolution moment of multi-population segregation

由于粒子群多样化后形成的每个子群体是围绕在1个局部最优周围形成的小环境，每个子群体应只含有1个最优解，没有陷入局部最优的顾虑，因此，对于每个子群体采用标准粒子群算法进行求解。

由于算法在经过位置更新后，很有可能会跳出当前的子群体，从而产生不属于该子群体的粒子。因此，在各子群体寻优一定代数后(本文取为10)，需要对所有粒子进行重新聚类分析。聚类分析的方法与第1.1节中所述方法相同。

在进行聚类分析后，新形成的各子群体中的粒子数会发生变化，需要进行子群体调整。对于粒子数大于cNum的子群体，按粒子适应值大小保存适应值最高的cNum个粒子;对于粒子数小于cNum的子群体，采用高斯变异方法生成新的粒子。算法如此循环，直至满足总的迭代次数，或者各子群体收敛到各自的最优解。

5 算法仿真及分析

为测试本文提出的多路径规划算法的正确性和有效性，使用VC++6.0实现算法，在不同的环境下进行仿真实验。

在算法运行过程中，粒子群初始规模设置为50个粒子。惯性权值w采用线性递减策略，在粒子群的多样化阶段，惯性权值w的变化范围取为wmax=0.5，wmin=0.2;在多群体隔离进化阶段，惯性权值w的变化范围取为wmax=0.95，wmin=0.2。参数c1和c2在算法中取相同数值2。粒子群多样化阶段的结束条件设置为每个子群体中的粒子数目不少于20个。多群体隔离进化阶段的结束条件设置为算法外循环迭代100次或各子群体均收敛。即若在100次迭代过程中，各子群体均收敛到各自最优解，则算法退出，否则，算法迭代100次后退出。

图4给出了多路径规划仿真实验的结果。

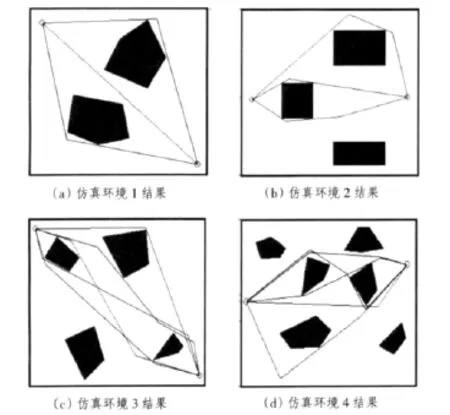
图4 多路径规划算法仿真实验结果Fig.4 Simulation experimentation result of multi-path planning method

由该仿真结果可以看到，本文设计的基于粒子群优化的多路径规划方法能正确有效的规划出多条路径。但同时也看到，当障碍物离环境边界较近或者环境较复杂时(例如仿真环境2～仿真环境4)，算法较难规划出绕过边界障碍的路径。这一问题的出现一方面原因是当障碍物离环境边界较近时，很难得到绕过障碍物和环境边界的可行路径，这就导致无法得到对应的子群体，因此无法规划出相应路径;另一方面原因是在评价路径的适应值评价函数中，往往将路径长度设置为主要的评价标准，而绕过边界障碍的路径一般会较长，因此无法得到与其相对应的路径。

6 结语

本文针对船舶全局多路径规划问题展开研究，在基本粒子群优化算法的基础上，引入聚类分析、隔离进化等策略实现多路径规划方法，给出了算法的设计思想、基本流程和主要设计内容，并针对多个仿真环境进行了仿真实验，得到结论如下:

1)基于粒子群优化的多路径规划方法能针对不同的环境模型进行环境划分，正确、有效的规划出多条运动路径。

2)当障碍物离环境边界较近或者环境较复杂时，算法较难规划出绕过边界障碍的路径，还有待进一步深入研究。

［1］张京娟.基于遗传算法的水下潜器自主导航规划技术研究［D］.哈尔滨:哈尔滨工程大学，2003.1－30.

［2］刘利强.蚁群优化方法研究及其在潜艇导航规划中的应用［D］.哈尔滨:哈尔滨工程大学，2007.8－25.

［3］MILLER B L，SHAW M J.Genetic algorithms with dynamic niche sharing for multi-modal function optimization［C］.Proc 3rdIEEE Conf.Evolutionary Computation.Piscataway，NJ:IEEE Press.1996.786 －791.

［4］刘铁男，陈广义，刘延力，徐宝昌.模拟生物种族形成的进化算法与多峰函数优化［J］.控制与决策，1999，14(2):185－188.

［5］SPEARS W M.Simple sub-population schemes［C］.proc.of the third annual conference on evolutionary programming.San Diego，1994.296 －307.

［6］KENNEDY J，EBERHART R C.Particle swarm optimization［A］.Proceedings of IEEE International Conference on Neural Networks.Piscataway，1995.193 －197.

Research on multi-path planning method based on particle swarm optimization

WANG Dan
(China Ship Research and Development Academy，Beijing 100192，China)

Based on the idea of genetic algorithm to solve the multi-modal function optimization，research of multi-path planning method based on particle swarm optimization has been carried out.Basic idea and algorithm flow of multi-path planning algorithm were given，methods of particle swarm diversified and evolution strategy of multi-population segregation were discussed，and simulation experiments aimed at multiple simulation environments were performed.Simulation result shows，multi-path planning algorithm in this article can make environment division aimed at different environmental models and plan multiple motion paths rightly and efficiently.

particle swarm optimization;multi-path planning;multi-population evolution

O221

A

1672－7649(2011)06－0156－04

10.3404/j.issn.1672－7649.2011.06.036

2011－05－06

王丹(1983－)，女，硕士，助理工程师，研究方向为导航、制导与控制。