乔列斯基分解应用于偏相干问题的可行性研究

章林柯，江 涌，何 琳

（1海军工程大学 振动与噪声研究所，武汉 430033；2防化研究院，北京 102205）

乔列斯基分解应用于偏相干问题的可行性研究

章林柯1，江 涌2，何 琳1

（1海军工程大学 振动与噪声研究所，武汉 430033；2防化研究院，北京 102205）

在应用传统的偏相干方法进行噪声源识别时，计算条件输入和耦合较为繁琐、复杂。文章首先通过对偏相干和乔列斯基分解的分析，得到两者之间的关系；进一步运用数学归纳法，从理论上证明了乔列斯基分解应用于偏相干问题的可行性；然后指出对归一化互谱矩阵进行乔列斯基分解，可直接得到各源的贡献比大小；最后给出了应用乔列斯基分解解决偏相干问题的一般步骤。舱段试验验证了该方法的可行性和实时性。

偏相干；噪声源识别；多输入/输出模型；乔列斯基分解

1 引 言

多输入/输出（MIMO）模型因其结构简单，且考虑了各点之间的相互关系，在噪声源的测量与分析中得到了广泛的应用[1-3]。对于MIMO模型，可以将其看成是由多个多输入单输出（MISO）模型构成的，所以在下面主要以MISO为例进行阐述。当各噪声源之间相互独立时，常相干方法就能够得到各源的贡献比大小。但当噪声源之间存在耦合时，常相干法会过高地估计各源的贡献比大小。而偏相干法能够扣除一定的耦合，正确地估计出各源的贡献比大小[4-5]。

偏相干方法要求首先对输入源进行排序，然后计算条件输入、输入和输出之间的耦合。计算条件输入和耦合的传统方法较为繁琐、复杂，影响了工程上的实时性。国内学者张宝成首先提到可用乔列斯基分解来解决偏相干问题[6]，但并未给出详细的理论证明。在输入源排序正确的前提下，本文将利用数学归纳法，得到乔列斯基分解的结果和偏相干解之间的关系，从理论上证明了可以利用互谱矩阵的乔列斯基分解得到各噪声源的贡献比大小。最后，舱段试验验证了该方法可以提高偏相干方法的实时性，方便偏相干方法的工程应用。

2 偏相干和乔列斯基分解的基本理论

2.1 偏相干法

偏相干分析的本质在于对输入进行一次线性变换，使得变换后的条件输入之间互不相关。在正确排序下，变换后的第一输入为原第一输入；变换后的第二输入为原第二输入扣除它与原第一输入相关分量的剩余，因而它与第一输入相互独立；以此类推，变换后第i输入为原第i输入扣除它与原第1，2，…，i-1输入相关分量的剩余，它与变换后1，2，…，i-1输入相互独立[1]。其变换前后的原理框图分别如图1和图2所示：

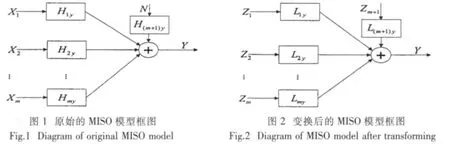
2.2 乔列斯基分解

在满足偏相干法的假设下，该矩阵是对称正定的，满足乔列斯基分解的条件[8]。分解使得Sxe=R′*R，其中R为上三角矩阵[9]，即

3 可行性证明

由（2）、（3）式可知，条件输入自谱Zii和耦合Lij必须循环迭代计算。即必须先计算Z11，才能计算L1j，然后才能计算Z22、L2j，如此反复。所以下面将用数学归纳法，得到乔列斯基分解结果和偏相干方法之间的联系，证明可用乔列斯基分解对偏相干问题进行求解。

由（6）式出发，可得

即上三角矩阵对角线上第一个元素的平方等于偏相干中第一条件输入的自谱。

由（2），（9）式可知，偏相干方法中第一个条件输入的自谱

当 i=1 时，由（7）式可得

对上式两边同时除以R11，结合（10）式可得

由上式可知，将上三角矩阵R的第一行元素除以其对角线上的元素R11，即可求得偏相干中输入和输出之间的耦合。即乔列斯基分解求得第一输入的贡献大小与偏相干求得第一条件输入的贡献大小相等。

假设i=l时，两种方法（乔列斯基分解、偏相干）得到的输入自谱和耦合相等，即

由（3）、（12）式可知，当i=1时，偏相干中输入和输出之间的耦合表示为

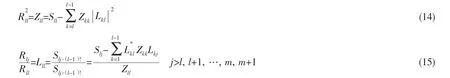
则当i=l+1时，由（8）式可知，乔列斯基分解可得

由（15）式可知，上式可改写成

由上式可知，上三角矩阵R对角线上第l+1个元素的平方等于偏相干中第l+1个条件输入的自谱。且当i=l+1时，由（7）式可知，乔列斯基分解可得

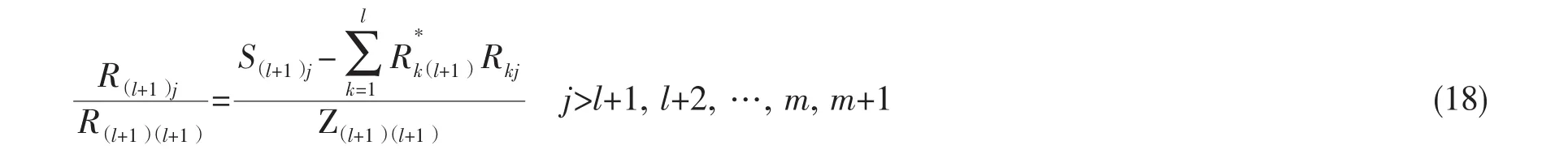
在偏相干方法中，条件互谱

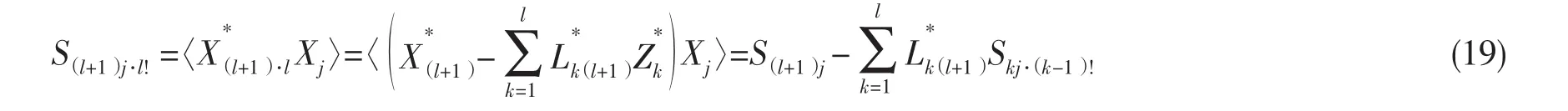
其中〈〉表示集平均。由（15）式可知

将（22）式代入（18）式中，可得

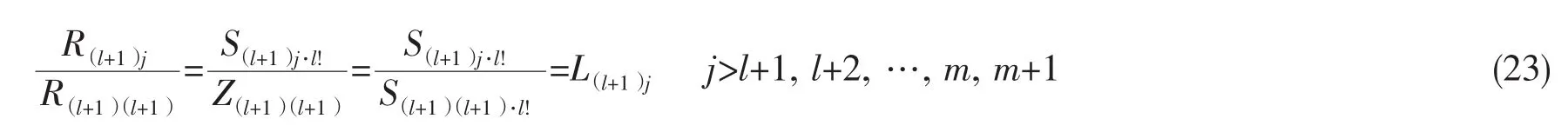
由上式可知，将上三角矩阵R第l+1行元素除以其对角线上的元素，即可得第l+1个条件输入与其他输入输出之间的耦合。综上所述，对输入输出的互谱矩阵进行乔列斯基分解，可求得偏相干中条件输入的自谱和耦合。

4 归一化的乔列斯基分解

4.1 一般的乔列斯基分解

由文献[10]可知，乔列斯基的分解式可以改写成

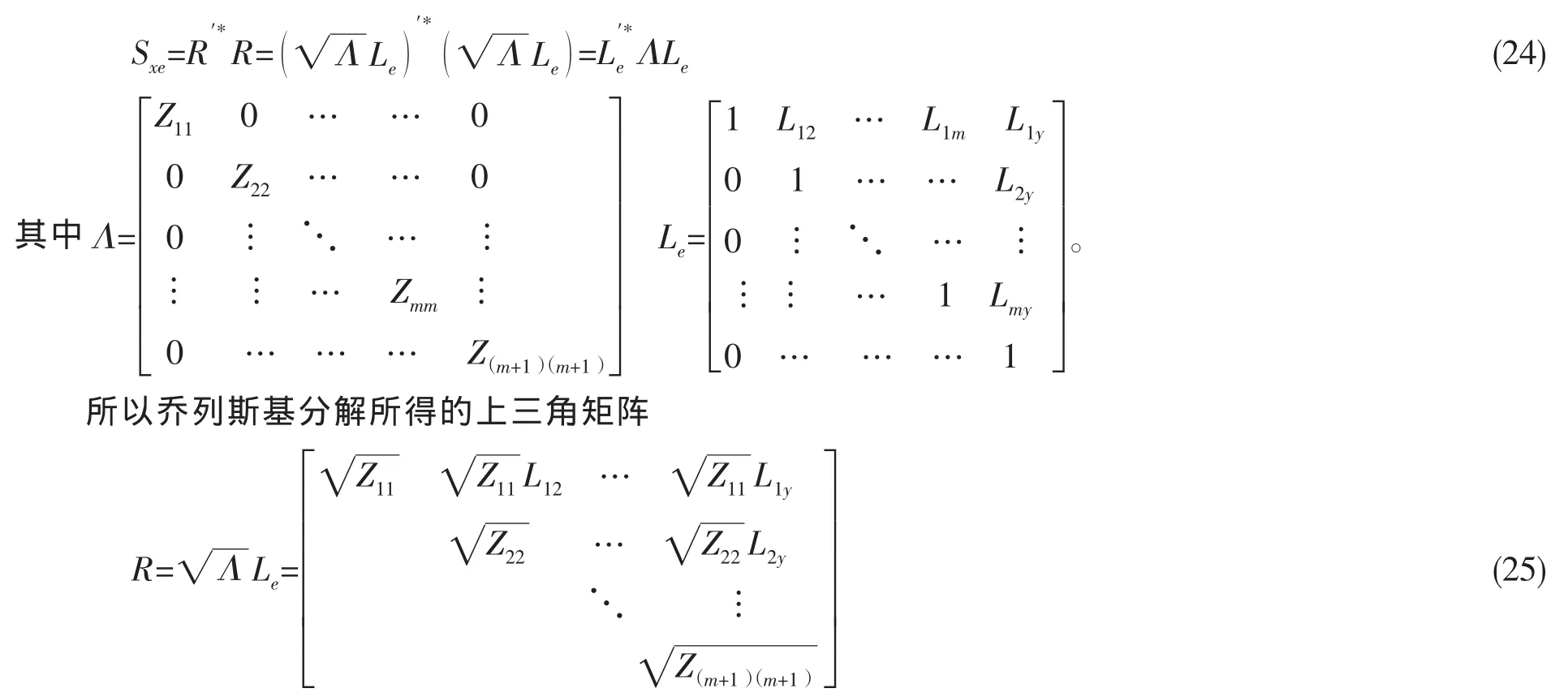
由偏相干可知，矩阵R最后一列元素的模的平方和等于输出自谱。因此，直接将矩阵R最后一列对应元素的模的平方除以输出自谱，即可得到对应输入的贡献比大小。

4.2 归一化的乔列斯基分解

与一般的乔列斯基分解不同，归一化的乔列斯基分解要求在分解前，先对互谱矩阵作归一化处理，即：将互谱矩阵的每一元素除以对应行对角元素的平方根和对应列对角元素的平方根，使得归一化的互谱矩阵的对角元素为1。即

G就称为归一化的互谱矩阵，其中rij为对应输入之间或输入输出之间常相干函数的平方根。

由上式可知，对上三角矩阵P最后一列对应元素取模、求平方，即可得到对应输入的贡献比大小，即pc（i）=（i=1,2,…,m,m+1 ）。且它们的和为1，其中最后一项为噪声的贡献比大小。因此，归一化分解的结果直观，易于理解。

4.3 乔列斯基分解求解偏相干问题的步骤

通过以上分析，总结出应用乔列斯基分解求解偏相干问题的步骤如下所示：

（1）对原始输入、输出数据时延补偿，然后计算其互谱矩阵Sxe；

（2）求取Sxe对角线上每一元素的均方根，构成矩阵d；

（3）计算归一化互谱矩阵G=d-1Sxed-1，然后对G进行乔列斯基分解，得到上三角矩阵P；

（4）对矩阵P最后一列的每一元素，计算其模的平方，就可以得到各输入源的贡献比大小。

通过以上步骤可以确定各源贡献比大小，当然这是在输入源的正确排序假设下。

5 试验研究

为验证上述算法的可行性和实时性，在舱段模型中进行了噪声源识别试验，模型如图3所示。在模型内安装有三个噪声源设备，分别为激振器、电机和海水泵。在设备的基座和内、外壳体上布置相应的加速度传感器，其中内壳上4个，外壳体6个。

激振器的频率360Hz，激励电压由150mV开始，每隔15mV递增一个工况到420mV。其中当激励电压增加到330mV时，将电机关闭。海水泵保持状态不变，总共工况为19个。采样频率为2 048Hz，采样时间为8s。

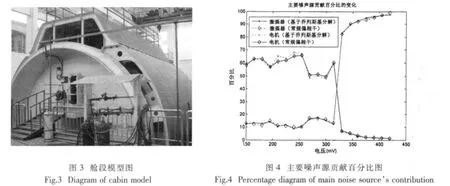
把设备基座上的测点作为输入，内、外壳上的测点作为输出。在对原始输入、输出数据时延补偿后，分别利用（2）、（3）式进行常规的频域偏相干分析，（26）、（27）式和（29）式进行基于乔列斯基分解的频域偏相干方法分析。其中外壳上16号测点作为输出时，主要噪声源贡献比大小如图4所示（为便于分析，只画出激振器和电机的贡献大小）。

由图4可知，两种方法（基于乔列斯基分解和常规的偏相干方法）得到主要噪声源的贡献比大小相互吻合，验证了乔列斯基分解应用于偏相干方法的可行性。

在电机关闭以前，激振器的贡献比随着激励电压的增大是振荡变化的。主要原因是在这些工况中，电机始终是主要噪声源。电机贡献比的变化导致激振器的贡献比发生相应的变化。当电机关闭后，激振器上升为主要噪声源。且其贡献比大小随着激励电压的增大而增大，说明该方法可用于噪声源贡献比的动态识别。

把内、外壳上的所有测点都作为输出，形成3输入10输出的MIMO模型。分别采用两种方法在PC机（CPU P4 2.4GHz）上进行分析，所用时间如表1所示。

表1 两种方法所消耗时间的比较Tab.1 Comparison of time consumption between two methods

由上表可知，基于乔列斯基分解的偏相干方法与常规的偏相干方法相比，时间节省了近2s。尤其是当实艇内、外壳体上部有大量的传感器时，基于乔列斯基分解的偏相干噪声源识别方法将可以提高源识别的实时性。

6 结 论

偏相干方法可以扣除输入源之间的一定耦合，在舰艇、汽车等的噪声源识别中得到了广泛的应用。本文运用数学归纳法，从理论上证明了乔列斯基分解应用于偏相干求解的可行性。并指出对归一化互谱矩阵进行乔列斯基分解，可直接得到各噪声源的贡献比大小。舱段试验验证了基于乔列斯基分解的偏相干噪声源识别方法的可行性和实时性。

由于上述结论是在各输入源正确排序下得到的，因此，输入之间的因果性检测（判断输入之间耦合产生的根本原因）就十分关键。由于只利用了信号的二阶统计信息，偏相干法只能解决同一频带上的单向耦合问题。对于同一频带上的双向耦合噪声源识别，因为盲信号处理可利用信号的高阶统计量，将是一个值得期待的方向。

[1]王之程,陈宗岐,于 氵风,刘文帅.舰船噪声测量与分析[M].北京:国防工业出版社,2004.

[2]陈声皖,章林柯,何 琳等.潜艇缓变声学故障预报研究[J].中国舰船研究,2010,5(3):18-21.

[3]陈心昭.噪声源识别技术的进展[J].合肥工业大学学报（自然科学版）,2009,32(5):609-614.

[4]左泽敏,李舜酩,郑娟丽.相关分析在机械振动信号处理中的应用[J].机械制造于维修,2009,38(1):75-79.

[5]陈茉莉,李舜酩.信号源识别的相干函数法[J].中国机械工程,2007,18(1):95-100.

[6]张宝成,徐雪仙.源贡献的时域分析方法[J].船舶力学,2001,5(4):54-60.

[7]贝达特J S.相关分析和谱分析在工程中的应用[M].凌福根,译.北京:国防工业出版社,1983.

[8]Bendat J S.Solutions for the multiple input/output problem[J].Journal Sound and Vibration,1976(44):311-325.

[9]何汉林,魏汝祥,李卫军.数值分析[M].武汉:湖北科学技术出版社,1999.

[10]张宝成,徐雪仙.舰船水下噪声相干测量和分析的发展过程—单输入/单输出和多输入/单输出比较[J].船舶力学,1999,3(5):68-79.

Study on the feasibility of applying Cholesky decomposition to partial coherence

ZHANG Lin-ke1,JIANG Yong2,HE Lin1
(1 Institute of Noise and Vibration,Naval University of Engineering,Wuhan 430033,China;
2 Institute of Chemical Defense,Beijing 102205,China)

The computation of conditional inputs and couplings is complicated when using traditional partial coherence methods to identify noise sources.In this paper,a simpler calculating method for engineering practice is presented.Firstly,the relationship between Cholesky decomposition and partial coherence was derived.Secondly,the feasibility of applying Cholesky decomposition to partial coherence calculation problems was validated by mathematical induction method.Then the percentage of each source’s contribution was determined after Cholesky decomposition of the normalized cross-spectral matrix.The process of applying Cholesky decomposition to partial coherence problems was proposed lastly.The feasibility and real time capability of this method was validated by cabin test.

partial coherence;noise source identification;multiple input/output model;Cholesky decomposition

TB567

A

1007-7294（2011）05-0556-07

2010-08-13 修改日期：2011-03-24

国家自然科学基金资助项目（50775218）；国防预研基金（9140A0050506JB11）

章林柯（1977-），男，海军工程大学博士，Email:zhanglk1999@gmail.com。