二阶灰色神经网络在船舶横摇预报中的应用
刘丽桑,彭侠夫
(厦门大学 自动化系,福建 厦门 361005)
二阶灰色神经网络在船舶横摇预报中的应用
刘丽桑,彭侠夫
(厦门大学 自动化系,福建 厦门 361005)
为了提高船舶的耐波性和适航性、对船舶横摇进行有效准确预报,提出了将灰色系统理论和神经网络进行有机结合的二阶灰色神经网络预报模型。介绍了二阶灰色预报模型,采用神经网络映射的办法构建灰色神经网络预报模型,并介绍了神经网络学习机制。另外,以某舰船横摇运动时间序列预报为例对模型进行仿真验证,有效改善了二阶灰色模型较大的预报偏差。仿真结果表明,GNNM(2,1)模型能准确预报船舶横摇运动,具有更高的预报精度和更好的数据稳定性。
灰色神经网络;船舶横摇;预报;GNNM(2,1)
1 引 言
灰色系统理论自80年代由邓聚龙[1]教授提出以来,已经在社会、经济、农业等领域取得了广泛的应用,并取得了一系列成果。它的特点是用灰色数学来处理不确定量使之量化,充分利用已知信息寻求系统运动的规律。其主要建模思想是将原始信息数据序列通过一定的数学方法处理后,将其转化为微分方程来描述原系统的客观规律。灰色理论在船舶运动预测上也取得了一定的成绩,如王淑娟[2]将MGM(1,n)模型用于舰船纵摇—升沉非线性运动预报;沈继红[3]用函数变换型GM(1,1)模型对船舶纵摇进行预报等。他们都是采用一阶灰色模型,通过对原始数列进行不同的预处理来提高预测精度,因而对预处理方法和原始数据要求较高。
本文将二阶灰色预测模型(GM(2,1)模型)与神经网络模型有机结合起来,建立一种新的二阶灰色神经网络预报模型(GNNM(2,1)模型),并在构建组合模型的基础上运用该模型对某船舶横摇运动进行预报;同时在模型预报速度方面和单纯神经网络预报、灰色模型预报及串联灰色神经网络预报等进行了分析比较。研究结果表明,二阶灰色神经网络模型比二阶灰色预测模型具有更高的精度和更好的数据稳定性,同时也具有较好的快速性。
2 二阶灰色神经网络数学模型
2.1 二阶灰色预测模型
由于船舶的摇动是一个往复摆动的过程,而GM(1,1)只有一个指数分量,随着时间的发展过程是单调的,反映不出摆动的情况。因此,为了能大致描绘船舶摇动数学模型,本文选择二阶灰色预测模型(GM(2,1))。 GM(2,1)具有两个特征根,也就是两个指数分量,能反映单调的、非单调的和摆动的(振荡的)情况[4]。

对应的白化方程为:

(2)式对应的齐次特征方程为 λ2+α1λ+a2=0,设 λ1、λ2为方程的两个不等实根,则 GM(2,1)常微分方程的解为:

(3)式也称为离散时间响应函数。
2.2 二阶灰色神经网络模型
人工神经网络具有强大的自学习、自组织和自适应能力以及处理非线性信息的能力。根据神经网络与灰色系统的融合方法的不同,目前可将灰色神经网络模型分为串联型、并联型和嵌入型3种结构[5-6]。传统的灰色模型采用最小二乘法来求解模型参数a1、a2和b,继而求解特征方程来得到模型预测值。本文采用神经网络映射的办法来求解模型[7]。将(3)式作以下变换:
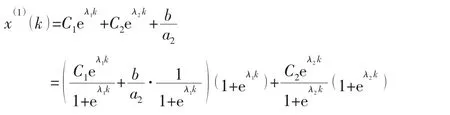
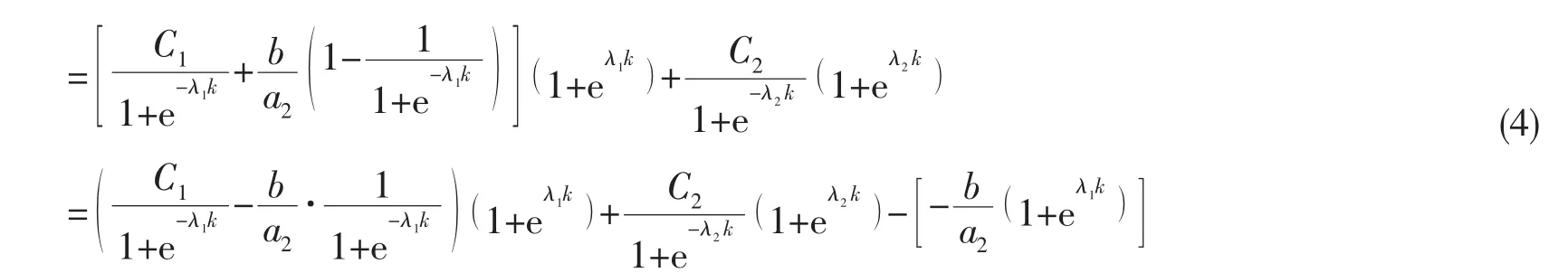
将(4)式映射到神经网络中,得到神经网络结构图(如图1)。如图所示,该网络结构为1-2-3-1,U、V、W 分别为 1×2、2×3、3×1 的权系数矩阵。 对于每一组(k, y(k )),k=1,2,…,n都有如下的BP神经网络学习步骤:
①输入网络初始权值和初始阀值:
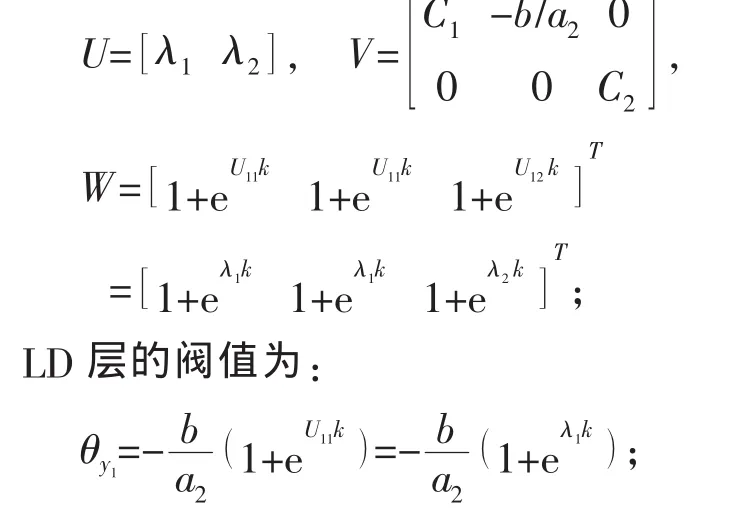

②计算各层的输出值:

⑤ 再次循环,s=s+1,重复上述②、③、④步骤,直至训练误差满足精度要求为止。
更新输入样本,直到所有样本训练结束,则训练好的网络可用于预测。
3 GNNM(2,1)的应用
以某舰船横摇运动为例,分别用灰色神经网络预测模型和二阶灰色预测模型进行预测。舰船特征数据如下:船长98m,船宽10.2m,正常排水量1 457.26t,平均吃水3.1m,初稳心高1.15m,横摇周期7.8s。图2是该舰在2级海况下,以12kns航速横浪航行时的横摇时间序列(取930个数据)。
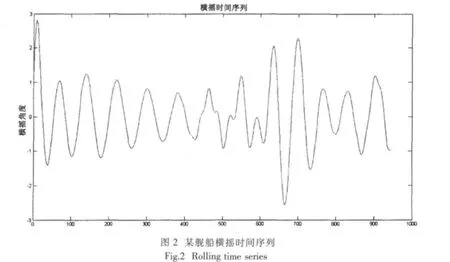
灰色神经网络预测模型以该横摇序列为训练样本和检验数据,分组进行训练,经反复论证,选取每组10个,并预测下5个;网络学习速率在0.01~0.8之间,惯性系数取0.9。二阶灰色预测模型则选取每组7个,预测下3个,同时选取新陈代谢因子为3,即第1~7个数据预测第8~10个,接着第4~10个数据预测11~13个,……以此类推,不断进行数据“新陈代谢”建模及预测,以便得到尽可能小的“尖刺”。设训练目标误差为10-4,输入层激活函数为tansig函数(也称S型函数),输出层激活函数为purelin函数。部分预测结果如图3所示。
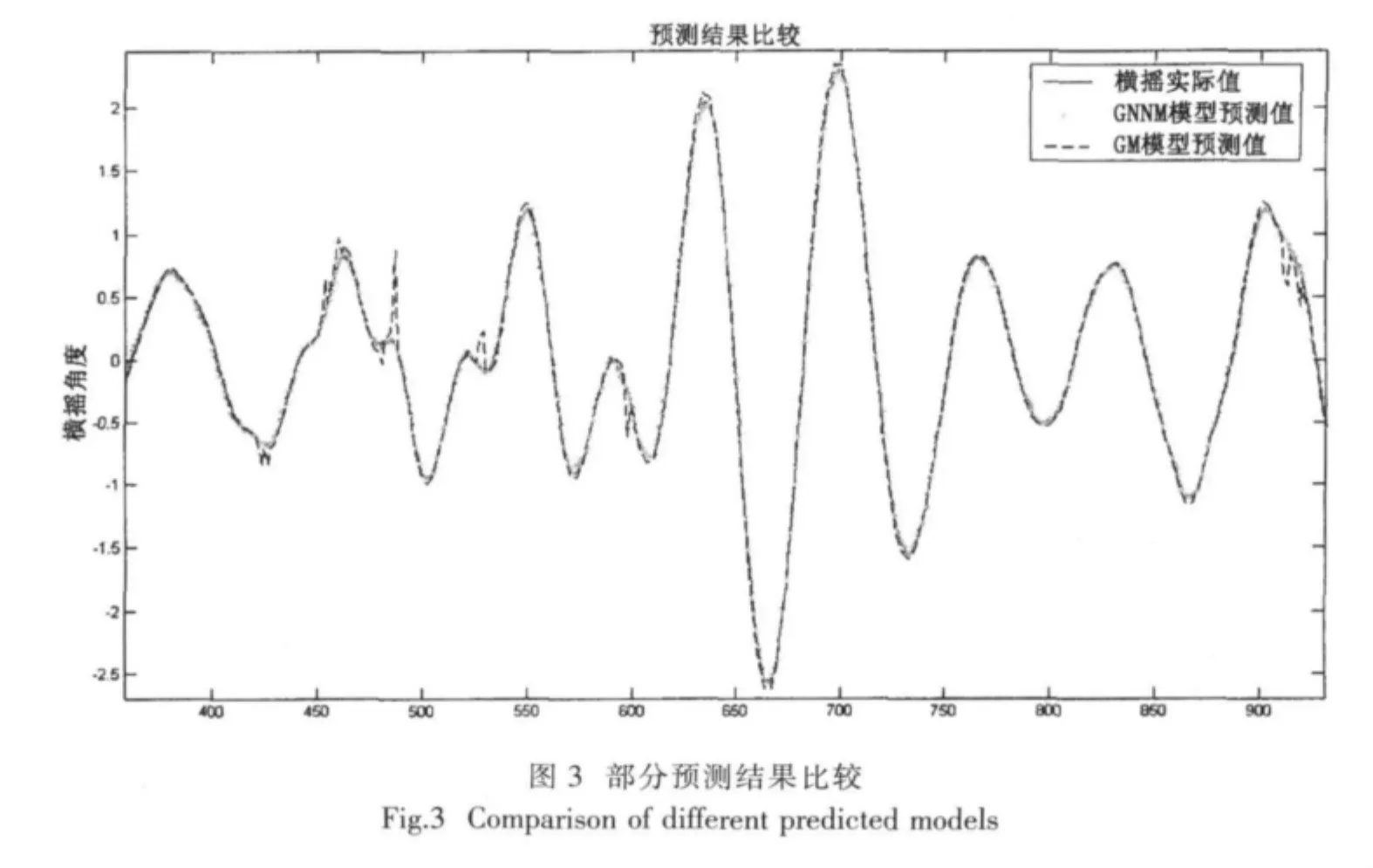
在这一时间序列预测仿真中,GNNM(2,1)模型和二阶灰色模型对前400个数据的预测精度基本相等,但二阶灰色模型对后半段数据的预测精度明显不如GNNM(2,1),甚至出现较大的偏差。从图3可以看到,GNNM(2,1)模型的预测精度要优于灰色模型的预测精度;在幅值和频率突变处,GNNM(2,1)能有效改善 GM(2,1)模型出现的“尖刺”现象。在同一误差精度要求下,GM(2,1)模型预测值的偏差的方差为0.35%,而GNNM(2,1)模型预测值的偏差的方差为0.17%,抖动幅度大大减小。
在预测速度方面,分别用灰色神经网络预测(GNNM)模型、二阶灰色预测(GM)模型、神经网络预测(NN)模型以及用BP神经网络补偿GM模型误差的组合模型(GM-NN)进行预测。从表1的比较可以容易得出,GNNM模型的预测速度要优于神经网络模型的预测速度,也要优于GM-NN组合模型的预测速度,可满足工程需求。
注:该程序执行时间均在同一PC机上单任务独立运行所得。

表1 不同模型的预测速度比较Tab.1 Comparison of running time
4 结 论
本文将灰色系统理论和神经网络有机结合起来,建立了灰色神经网络(GNNM(2,1))模型,同时有效地对船舶横摇运动进行建模及预测。仿真结果表明,GNNM(2,1)模型克服了二阶灰色预测模型在幅值和频率突变时有较大预测误差的不足,同时有效减小预测值的抖动偏差,预测结果更具有稳定性。
[1]邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.
[2]王淑娟.基于灰色多因素预测模型MGM(1,n)的舰船非线性运动预报[D].哈尔滨:哈尔滨工程大学,2007.
[3]沈继红.舰船纵摇运动函数变换型GM(1,1)模型研究[J].哈尔滨工业大学学报,2001,33(3):291-294.
[4]刘思峰,党耀国,张岐山.灰色系统理论及其应用[M].北京:科学出版社,1991.
[5]袁景凌,钟 洛,李小燕.灰色神经网络的研究及发展[J].武汉理工大学学报,2009,31(3):91-93.
[6]Zhong Luo,Yuan Jingling,Xia Hongxia,et al.A study on Gray Neural Network Modeling[C]//Proceedings of the First International Conference on Machine Learning and Cybernetics.Beijing,China,2002:2021-2023.
[7]Song Huazhu,Han Bo.Neural network modeling study of one dimension gray problem GNNM(1,1)[C]//Info-tech and Info-net Proceedings ICII.Beijing,2001(3):491-497.
Second order Gray Neural Network in ship roll forecast
LIU Li-sang,PENG Xia-fu
(Department of Automation,Xiamen University,Xiamen 361005,China)
To enhance the ship’s seakeeping capacity and seaworthiness,a second order Gray Neural Network forecasting model is presented to forecast roll motion accurately.The gray system and its gray model are introduced,then using neural network mapping approach to build the second order GNNM(2,1)model.On the other hand,the learning algorithm is presented.Further more,GNNM(2,1)is applied in a sample of ship roll series and effectively improves large prediction error of second order gray model.The simulation results prove that the new model is more accurate and stable than tradition models.
Gray Neural Network;ship roll;forecast;GNNM(2,1)
U661.3
A
1007-7294(2011)05-0468-05
2011-01-05
985工程学科建设项目(0000-x07204)
刘丽桑(1984-),女,厦门大学自动化系博士研究生,主要从事船舶运动控制,虚拟现实技术等研究,Email:liulisang@163.com;
彭侠夫(1963-),男,教授,博导,主要从事控制理论及应用、船舶运动综合控制技术等研究,Email:pengxiafu@163.com。

