基于RANS方程的对拍翼推进器推进性能分析
于宪钊,苏玉民,王兆立
(哈尔滨工程大学 水下机器人技术国防科技重点实验室,哈尔滨 150001)
基于RANS方程的对拍翼推进器推进性能分析
于宪钊,苏玉民,王兆立
(哈尔滨工程大学 水下机器人技术国防科技重点实验室,哈尔滨 150001)
文章基于RANS方程,应用动网格技术,数值计算分析了一种基于地效应原理的对拍翼推进器的推进性能,探讨了来流速度,拍动频率、振幅对推进性能的影响。计算结果表明拍动频率越高、拍动振幅越大则推进器的推力越大,而推进效率则会随来流速度以及拍动振幅的增大而呈现先增大后减小的趋势;同时对比分析了双翼对拍与单翼拍动产生的推力和推进效率;这种推进器构造简单,仅通过简单的相对拍动就可产生垂直于机翼轴向的推力,通过机翼的旋转就可产生任意方向的推力,能够满足水下机器人做六自由度运动的推力需求。
推进性能;仿生推进器;拍动翼;动网格
1 引 言
水下机器人作为水下高技术设备的集成体,在海洋科学研究、军事、商业领域都有着广阔的应用前景。微小型水下机器人更以其体积小、机动灵活、隐蔽性强、噪声低的特点成为目前研究的热点,而具有良好推进性能的推进装置是这些特点的重要保障[1]。
鱼类和鸟类经过长期的自然选择和进化拥有了非凡的水中游动能力和空中飞翔能力,其运动的高效率、低噪声、高速度、以及高机动性引起了各国学者的关注,尤其是水下机器人领域的学者更将其作为模仿的对象。1994年麻省理工学院模仿金枪鱼制造的RoboTuna,开始了研究鱼类高效游动奥秘的工作[2]。中国科学院生物运动力学实验室提出了以理论模化方法对昆虫飞行和鱼类游动进行生物外部流体力学研究[3];美国Cornell University研究了空气中昆虫的拍翼模型,数值分析结果表明二维拍翼模型产生的起动力优于三维模型[4];南京航空航天大学进行了仿生扑翼飞行机器人翅型的研究,探讨了扑翼机构的流体试验平台的构建[5];1996年Jones等人采用面元法分析了拍动翼尾迹中放置机翼对推力性能的影响,并进行了相关的实验研究[6];1997~1999年Jones采用二维面元法计算了拍动翼的推进性能,并进行了相关的实验研究,结果表明双翼对摆较单翼摆动能提供更高的推力,而且效率更高[7-8];2002年Jones和Platzer又对基于地效应机理的拍动翼的推进性能进行了实验和数值计算上的研究[9];最近的研究是2005年刘鹏飞采用三维面元法计算了对摆式推进器的推力和效率,系统地讨论了频率、振幅、双翼间距、展弦比对推进性能的影响,同时证明了双翼对拍较单翼拍动具有更高的效率[10]。
由于机械设计上的困难,大多数的仿生推进器都采用了摆动式,而对对摆式推进器则研究相对较少,同时由于对摆式推进器需要较大的翼展才能保证推力的要求,因而增大了机械设计和布置的困难使这种推进方式难于实际应用,但不同于传统的螺旋桨(推力方向平行于轴向),这种新型的推进器仅通过简单的相对拍动就能产生垂直于机翼轴向的推力,通过机翼的旋转就可以产生任意方向的推力,其良好的操纵特性和简单的传动方式能够满足水下机器人做六自由度运动对推力器的要求,具有一定的研究和应用价值。
目前对于对摆式推进器的研究多集中在采用面元法,而不考虑粘性的影响。随着计算技术的迅速发展,计算机性能的提高,CFD(Computational Fluid Dynamics)的发展日趋成熟,数值求解粘性Navier-Stokes方程的精度也越来越高,种类繁多的计算流体力学软件更以其通用性和易操作性被广泛应用在工程开发、科学研究的各个领域。哈尔滨工程大学苏玉民、杨亮、王兆立等就采用计算流体力学软件对鱼类的尾鳍、胸鳍的水动力性能进行了详细的数值计算和实验研究,获得了良好的效果[11-12]。
本文首先建立了一种对拍翼推进器模型;然后采用Standard k-ε二方程模型求解RANS方程,计算了该推进器的推进性能;最后分析了来流速度、拍动频率和振幅对推进性能的影响。通过与Jones、Platzer和刘鹏飞的工作相对比,验证了文中采用方法的正确性和准确性,同时通过数据对比分析进一步验证了这种对拍翼推进器的良好推进性能。
2 数值计算基本原理和方法
2.1 数值计算模型和运动规律的提出
计算采用的拍动翼翼型为NACA0014翼型,采用适应性较强的非结构网格离散计算区域,网格数量分别为23 374,51 018,网格布置内密外疏,以同时保证机翼表面附近网格密度和整体网格的弹性,如图1所示。

式中h0为拍动翼拍动振幅,y0为对拍翼平衡位置的间距,ω为机翼拍动圆频率,ω=2π f;为同文献[8,10]相比较,取 h0=0.4c,y0=1.4c,机翼弦长 c=0.064m,介质粘度υ=1.57*e-5,坐标系统如图2所示。
2.2 数值计算方法
采用Standard k-ε模型求解RANS方程,封闭后的方程组为:

拍动双翼的运动规律相同,速度相反,其运动方程为:
式中湍流粘度定义如下:

模型中的常数取值如下:Cμ=0.09,C1ε=1.44,C2ε=1.92,σk=1.0,σε=1.3。
采用SIMPLE算法求解压力速度耦合方程组,对流项以二阶迎风格式离散,用标准壁面函数求解机翼表面边界层内的流动。由于拍动翼振幅较小,频率较大,因此需要很小的时间步长,以保障网格质量,进而保证计算的精度,对应不同的拍动频率,本文中每个周期迭代5 000~10 000步。
本文采用动网格方法,基于弹簧变形原理实现了机翼对拍非结构网格的变形移动和网格光顺,保证了机翼表面附近的网格质量。
基于弹簧原理的网格光滑方法,其基本思想是将连接任何两网格节点的网格边理想化为弹簧。根据虎克定律,节点上的力可表示为:

式中Δxi,Δxj为节点i以及它的相邻节点j的位移,ni为节点i的相邻节点数,kij是节点i,j间弹簧的刚度系数,定义为:

节点位移则按下式迭代更新:

在计算时将弹簧刚度系数设置为0,这样在机翼运动过程中,机翼附近的网格不变(单翼拍动)或变化很小(双翼相对拍动),而仅是机翼远端网格变形,这样保证了网格质量和计算精度;对于双翼对拍的情况,双翼间距随时间变化,网格质量会变差,因此加大了双翼间的网格密度,以保证网格质量。
3 数值计算结果
3.1 单翼拍动和双翼对拍的推力性能分析
首先计算了频率为8Hz时单翼拍动的推力系数Ct,Ct及侧向力系数Cl定义如下:

式中V∞为自由来流速度,ρ为介质密度,ρ=1.225kg/m3,pl为dl段拍翼受力。
从图3可见,随着来流速度的增大单翼拍动产生的推力系数在减小,同Jones、Platzer以及刘鹏飞面元法的计算结果规律一致,但由于计算中考虑了粘性的影响,采用求解RANS方程的方法的计算结果要比面元法的小。
图4对比了拍动频率为8Hz时单翼拍动和双翼对拍的推力系数,数值计算的结果同实验结果显示出了同样的规律,计算结果清晰地显示了对拍双翼较单翼拍动产生了更大的推力,同时随着来流速度的增大,推力系数减小,说明在低速下对拍翼的推进性能更优。
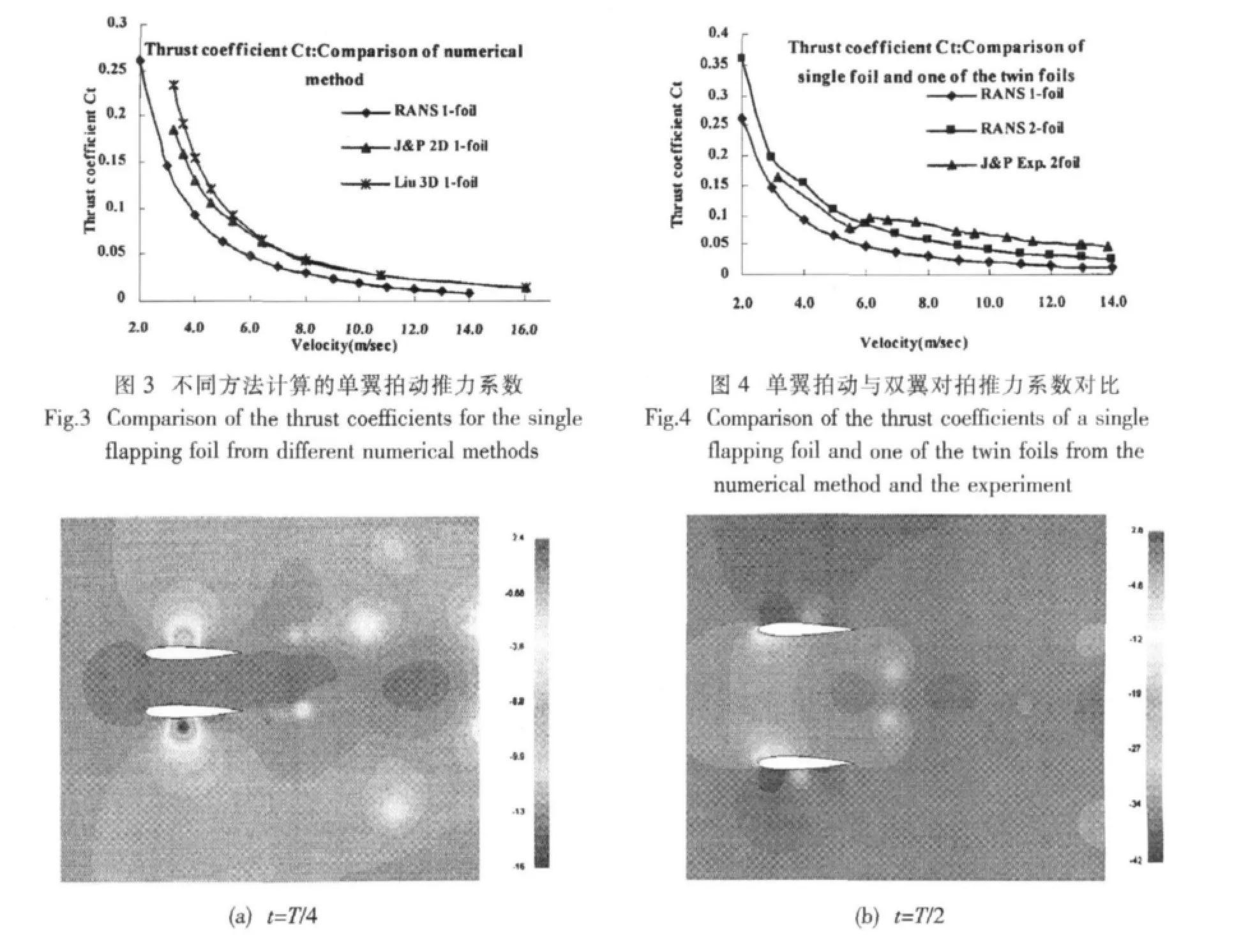
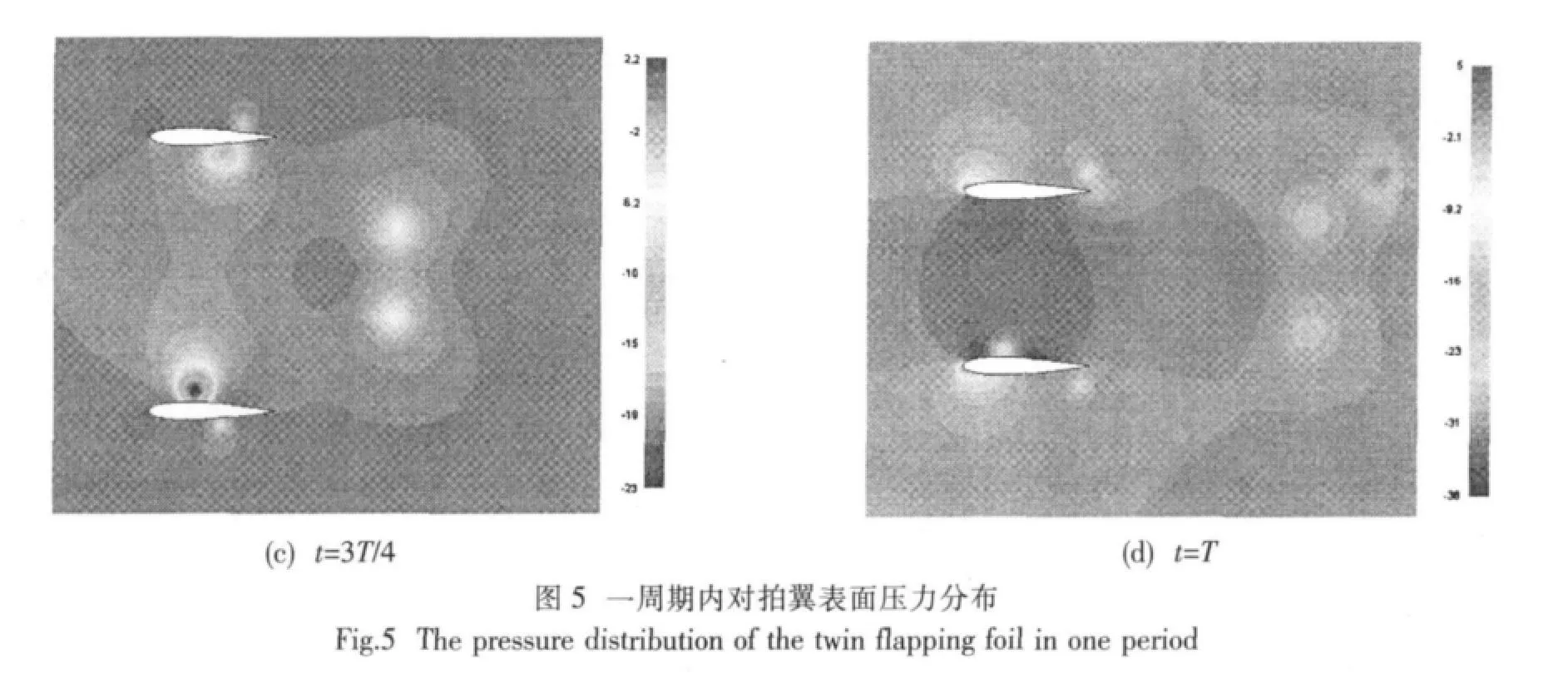
对拍双翼在一个拍动周期内机翼表面压力分布如图5所示,图中显示了机翼拍动过程中尾涡的形成和脱落过程。
双翼对拍的推力系数和侧向力系数曲线如图6、7所示,从中可以看出推力系数和侧向力系数均呈正余弦规律变化,随着来流速度的增大,推力系数和侧向力系数都在减小,同时推力系数的变化周期约为侧向力系数变化周期的一半。

3.2 单翼拍动和双翼对拍的推进效率分析
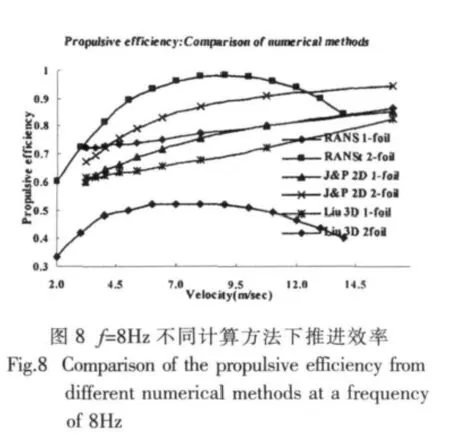
拍动频率为8Hz时,不同的数值计算方法计算的单翼拍动和双翼对拍的推进效率如图8所示。
推进效率采用(13)式计算:

其中f为机翼拍动频率,Δs为每一时间步长内机翼的位移。
同Jones、Platzer以及刘鹏飞面元法的计算结果相对比,可见面元法的计算结果认为随着来流速度的增大,推进效率在增大,但求解RANS方程的结果则是随来流速度的增大推进效率先增大后减小,在来流速度为10m/s附近存在效率的最大值,在这一点上,主要是由于采用不同的数值方法分析这一问题时,计算效率的公式也都不尽相同,但不同的数值方法都显示了双翼对拍的推进效率要明显高于单翼拍动的推进效率,这是研究的主要方面。
3.3 拍动振幅改变时单翼拍动和双翼对拍的推进性能分析
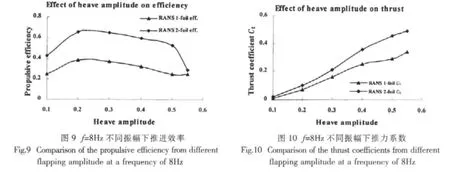
图9、图10显示了拍动频率为8Hz,来流速度为2m/s,不同拍动振幅下的推力系数和推进效率,比较计算了振幅为0.1~0.55倍弦长时的推进性能。由图可见,随着拍动振幅的增大,推力系数在增大,推进效率则是先增大后变小,在振幅为0.2倍弦长附近有推进效率的最大值,同时双翼对拍产生的推力和推进效率都明显高于单翼拍动的结果。
3.4 拍动频率变化时双翼对拍的推进性能
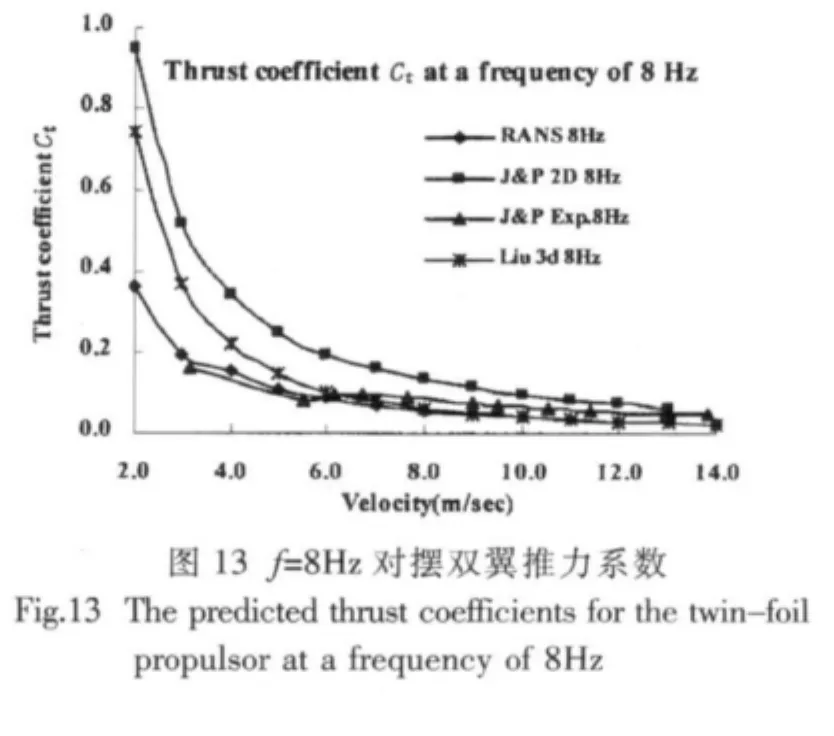
为了使该推进器能更好地用于水下机器人的运动仿真和控制,针对其特点本节重点研究了在不同拍动频率下双翼对拍的推力性能。图11~13显示了拍动频率分别为4Hz,6Hz,8Hz时双翼对拍产生的推力情况,并同Jones、Platzer的二维面元法、实验以及刘鹏飞的三维面元法结果相对比。

通过上述对比分析得知,随着拍动频率的增加,拍翼产生的推力也在增大,同时由于粘性的影响,求解RANS方程方法的结果较面元法的结果小,且更接近实验结果。
通过上述大量数值模拟得知该计算方法能够较好地模拟该推进系统的水动力性能,计算结果可以用于微小型水下机器人的推进系统开发和研究。
4 结 论
本文采用动网格技术,求解RANS方程,计算了一种对拍式推进器的推进性能,比较了来流速度、拍动频率和拍动振幅对推进性能的影响,通过与Jones、Platzer的二维面元法和实验结果以及刘鹏飞的三维面元法的计算结果相对比,验证了这种新型推进器的优良推进性能。计算结果表明双翼对拍产生的推力和推进效率都明显高于按照相同规律运动的单翼拍动;随着来流速度的增大,双翼对拍产生的推力系数在下降,推进效率先增大而后减小;同时拍动频率越高,相应产生的推力也越大;拍动振幅越大,产生的推力就越大,但推进效率却呈现是先增大后减小的趋势。
[1]苏玉民,万 磊,李 晔,庞永杰,秦再白.舵桨联合操纵微小型水下机器人的开发[J].机器人 ROBOT,2007,29(2):151-154.
[2]Trian Tafyllou M S,Trian Tafyllou G S.An efficient swimming machine[J].Scientific,1995,272(3):64-70.
[3]童秉纲,陆夕云.关于飞行和游动的生物力学研究[J].力学进展,2004,34(1):1-8.
[4]JaneWang Z,Birch J M,Dickinson M H.Unsteady forces and flows in low Reynolds number hovering flight:two-dimensional computations vs robotic wing experiments.Journal of Experimental Biology[J].2004,207:449-460.
[5]王姝歆,陈国平.仿生扑翼飞行机器人翅型的研制与实验研究[J].实验力学,2006,21(3):315-321.
[6]Jones K D,Dohring C M,Platzer M F.Wake structures behind plunging airfoils:A comparison of numerical and experiment results[J].AIAA Paper No.96-0078,1996.
[7]Jones K D,Platzer M F.Numerical computation of flapping-wing propulsion and power extraction[J].AIAA Paper No.97-0826,1997.
[8]Jones K D,Platzer M F.A experimental and numerical investigation of flapping-wing propulsion[J].AIAA Paper No.99-0995,1999.
[9]Jones K D,Castro B M,Mahmoud O,Platzer M F.A numerical and experimental investigation of flapping-wing propulsion in ground effect[J].AIAA Paper,No.2002-0866,2002.
[10]Liu Pengfei.Propulsive performance of a twin-rectangular-foil propulsor in a counterphase oscillation[J].Journal of Ship Research,2005,49(3):207-215.
[11]王兆立,苏玉民,李彦丽,杨亮,王晓飞.非定常流场中机械胸鳍的水动力性能分析[J].哈尔滨工程大学学报,Journal of Harbin Engineering University,2009,30(5):536-541.
[12]杨 亮,苏玉民.粘性流场中摆动尾鳍的水动力性能分析[J].哈尔滨工程大学学报,2007,28(10):1073-1078.
Propulsive performance analysis of a twin-flapping-foil propulsor based on RANS equations
YU Xian-zhao,SU Yu-min,WANG Zhao-li
(State Key Laboratory of Autonomous Underwater Vehicle,Harbin Engineering University,Harbin 150001,China)
In this paper,the propulsive performance of a twin-flapping-foil propulsor in ground effect was calculated based on the RANS equations;dynamic mesh method was applied in numerical calculation.The calculation included the effects of the number of foils(single versus double),freestream velocity,flapping frequency and amplitude to the propulsive performance.Numerical calculations showed that the thrust increased with the increasing of flapping frequency and amplitude,but when the freestream velocity or the flapping amplitude increased,the propulsive efficiency increased first and decreased then.The thrust and propulsive efficiency were also compared of single foil with twin foils.This simple thruster can generate thrust perpendicular to the foil’s shaft by flapping without pitching motion,a thruster vector of any direction can be generated by rotating the foils,which can satisfy the thrust requirement of the underwater vehicle in six degree of freedom motion.
propulsive performance;biological propulsor;flapping foil;dynamic mesh
U661.33+6
A
1007-7294(2011)05-0449-07
2010-03-03 修改日期:2010-10-27
国家自然科学基金资助项目(50879014,50579007)
于宪钊(1983-),男,博士生,研究方向为微小型水下机器人在复杂流场中的运动性能分析;
苏玉民(1960-),男,教授,博士生导师。

