玻璃模具型腔等离子喷焊机器人运动仿真研究

王 倩，周一丹，周自强，张兴国

（1. 南通大学 机械工程学院，南通 226019；2. 常熟理工学院，常熟 215500）

玻璃模具型腔等离子喷焊机器人运动仿真研究

王 倩1，周一丹1，周自强2，张兴国1

（1. 南通大学 机械工程学院，南通 226019；2. 常熟理工学院，常熟 215500）

根据玻璃模具型腔等离子喷焊的工作条件和任务要求，对用于玻璃模具型腔等离子喷焊的机器人进行了参数设计，讨论了该机器人的运动学问题。在MATLAB环境下，用 Robotics toolbox对该机器人的正运动学、逆运动学、轨迹规划进行了仿真。通过仿真，观察到了机器人各个关节的运动，并得到了相关数据，表明了设计参数的合理性。

玻璃模具型腔；等离子喷焊；机器人；轨迹仿真；MATLAB

0 引言

目前企业在玻璃模具生产中的一个重难点是要进行玻璃模具型腔关键部位的等离子喷焊以提高其耐磨、耐腐蚀和抗氧化等性能[1]，而现有的操作都是人工完成，工人需要将经过预热的玻璃模具（温度高达650℃～700℃，重约15Kg）搬上或搬下焊机工作台，导致了工人劳动强度大，工作效率低且存在着极大的安全隐患。为解决这一问题，拟采用机器人代替人工操作，对其进行了参数设计、运动学和轨迹规划的仿真，尤其是对于小批量多品种（有时甚至是单件）的玻璃模具来说，提出了基于玻璃模具的CAD图形直接生成喷焊机器人的运动轨迹而省略了现有的机器人示教或离线编程工作，将大大简化了机器人的工作方式，提高了生产效率。这也符合信息集成的理念。

1 玻璃模具等离子喷焊机器人参数设计

根据企业玻璃模具等离子喷焊的整个过程要求，提出了玻璃模具型腔全过程自动喷焊系统方案，其由等离子喷焊机、机器人、玻璃模具电感加热炉、供料传送带和成品存放区构成，如图1所示。

根据图1所示系统布局方式和机器人所要完成的工作任务，机器人的结构方案采用柱面坐标式机器人，如图2（a）所示。主要由底座、立柱、水平手臂和末端执行器构成。水平手臂装在立柱上，能水平方向上自由伸缩，并可沿立柱上下运动。立柱安装在底座上，并与水平手臂一起能在底座上转动。其中前两个为移动关节，最后一个为转动关节，这三个关节确定了末端执行器的位置。在手臂末端的手腕处还有两个转动自由度，实现末端执行器的姿态—俯仰和旋转。此机器人取名为“robot-glass mould”。该柱面坐标式机器人位置精度高，控制简单。其动作过程如图3所示。

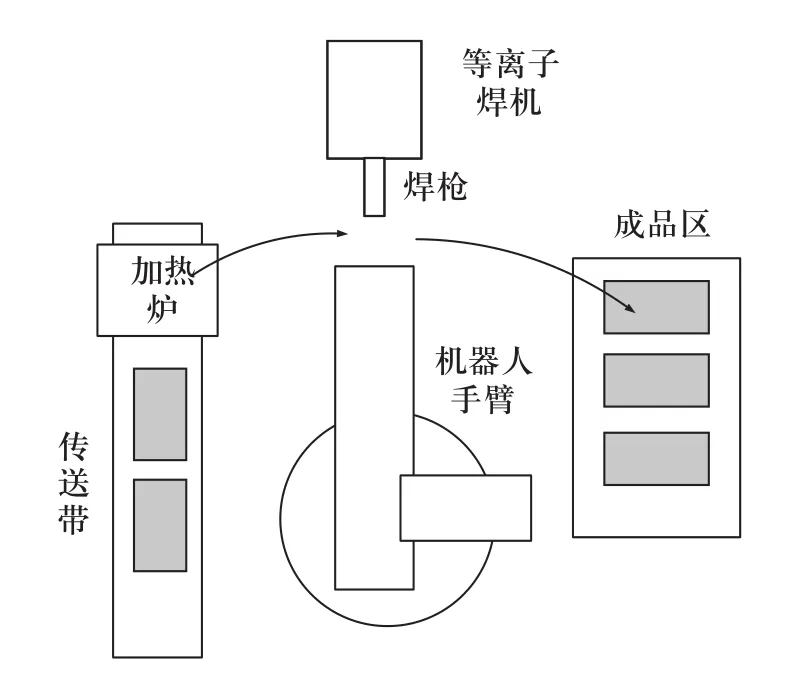
图1 等离子喷焊机器人系统平面布局示意图

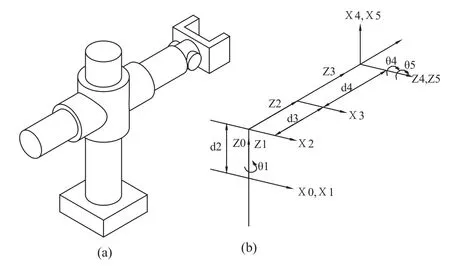
图2 “robot-glass mould”的实体模型及连杆坐标系

图3 等离子自动喷焊机器人动作流程图

按照机器人的整个动作过程和模具型腔全过程自动喷焊系统布局方案，表1给出了“robotglass mould”的连杆参数。其中，具体的参数d2，d3及d4是由预定的工作任务决定的，其余均按D-H变换[2]的定义进行设计。

表1 “robot-glass mould”的连杆参数

2 玻璃模具型腔等离子喷焊机器人运动学仿真算法

2.1 机器人运动学正问题

所谓运动学正问题[2,3]就是对于一机器人，给定杆件的几何参数和关节的位移，求解末端连杆坐标系相对于基坐标系的位姿。

为求解运动学方程式，用齐次变换矩阵i－1Ti来描述第i坐标系相对于（i－1）坐标系的位置和方位，记作：

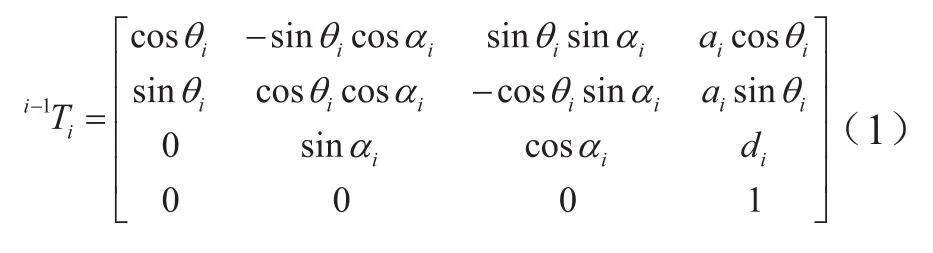
现在，将机器人的参数代入式（1），得到第i坐标系相对于机座坐标系位姿的齐次变换矩阵0Ti，表示为：

特别的当i＝5时，可求得0T5，它确定了机器人的末端相对于基坐标系的位置和姿态。表示为：

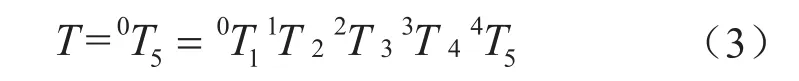
其中

2.2 机器人运动学逆解

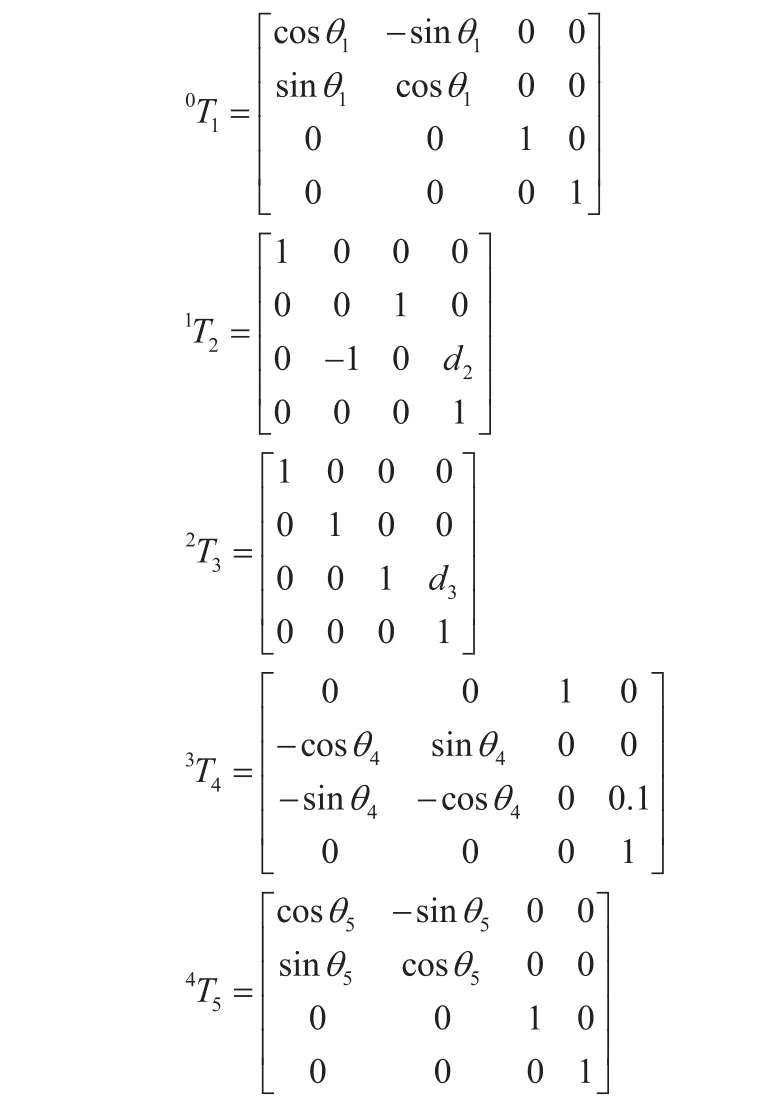
机器人运动学逆问题就是已知末端连杆的位置和方位，求得机器人的各个关节变量，对于上述的“robot-glass mould”，需要求解的变量为q1，d2，d3，q4，q5。

机器人运动学逆问题的求解方法是：将运动方程式（3）的两端依次左乘各T矩阵的逆矩阵，并使两端相等矩阵的对应元素相等，即可求得各关节变量。

求解关节变量的方程式如下：

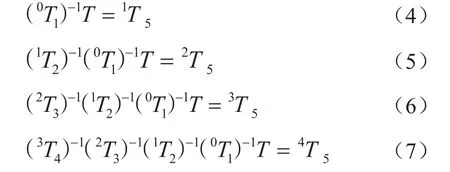
3 玻璃模具型腔等离子喷焊机器人轨迹规划

机器人轨迹规划是根据机器人要完成的任务设计机器人各关节的运动规律。例如，对一般的工业机器人来说，操作员可能只输入机械手末端的目标位置和方位，而规划的任务便是要确定出达到目标的关节轨迹的形状、运动的时间和速度等。这里所说的轨迹是指随时间变化的位置、速度和加速度。轨迹规划主要有两种方案[3]：1）点到点运动（PTP）轨迹规划；2）连续路径运动（CP）的轨迹规划。对于连续路径运动，不仅要规定机械手的起始点和终止点，而且要指明两点之间的若干中间点 （称路径点），必须沿特定的路径运动（路径约束）。

玻璃模具型腔等离子喷焊机器人将玻璃模具从预热部位（设为点A）移动到等离子焊机下（设为点B），喷焊完成后再将其放到货架区(设为点C)的运动路径没有要求，属于PTP规划。在喷焊过程中喷焊轨迹要沿着焊缝，因此属于CP规划。

4 MATLAB运动仿真

4.1 运动仿真

1）在对上述规划轨迹进行仿真前，先使用link函数和robot函数建立机器人模型，用r.name为机器人命名为“robot-glass mould”。

命令如下：

2）按预定PTP轨迹进行仿真（由于篇幅有限，仅对A点到B点进行仿真示例），A点可表示为qA=[0 0 0 0 0]，即表示机器人的各个关节都处于零位置处。机器人在B点相对于基坐标系的位姿可用TB表示。然后，按运动学逆问题的解决方法，可以求得A到B的各个关节变量。下面用Robotics toolbox的逆运动学命令ikine( )来求解：

%说明机器人由A到B，关节1需正向转动1.5708rad，关节2和3需向前移动0.2m和0.5m，最后两个关节需分别逆向转动3.1416rad和正向转动1.5708rad。

3）用命令plot（ ）对机器人由A 到B 的运动进行仿真（取仿真时间为2s，采样间隔时间为0.056s），这时就可以看到机器人各关节的具体运动情况，图4给出了机器人运动到B时的三维图。命令如下：

图4 “robot-glass mould”运动到B点时的三维图

4）按预定CP轨迹进行仿真

现有机器人可以通过示教喷焊区域的特征点，经过轨迹规划算法和逆运动学计算，得出喷焊区域的机器人喷焊仿真和实际喷焊操作，但是对于目前多品种小批量的玻璃模具来说，直接通过玻璃模具的AutoCAD图纸文件得出机器人的喷焊操作将会大大提高生产效率，其设计思想流程见图5所示。

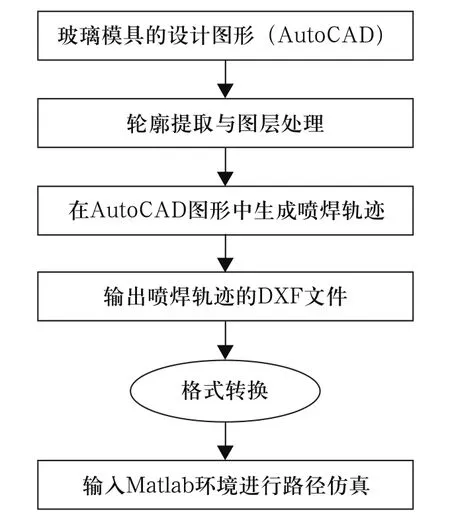
图5 焊缝喷焊轨迹规划仿真思路流程图

由于MATLAB从7.0版本就提供了一个实用的用户图形界面开发程序guide，它完全支持可视化编程，类似于Visual basic，因此，用户可以十分方便地设计出高质量的图形用户界面（GUI），设计的玻璃模具型腔等离子喷焊机器人的仿真界面如图6所示。

图6 玻璃模具型腔等离子喷焊机器人仿真界面

4.2 仿真结果分析

从运动仿真的前两步，可以看出机器人前三个关节的运动可以满足通常三自由度柱面坐标机器人的运动要求，即手臂可以实现水平方向上的自由伸缩，绕立柱的转动和沿立柱的上下运动，从而验证了连杆1，2，3的连杆参数设计的合理性。机器人后两个关节的运动可以使末端关节具有不同的姿态（实现俯仰和旋转），也说明了设计的参数是合理的。

在运动仿真的第（3）步，我们观察到机器人由A运动到B时各个关节的运动情况（文中无法显示这一运动过程），且各个关节运动情况均为正常，各连杆没有运动错位的情况，从而验证了所有连杆参数的合理性，且各参数的设计能够实现预定的目标。

在图6所示的仿真界面中，逆运动学仿真得到的5个关节的运动情况也是合理的。

5 结束语

根据玻璃模具型腔等离子喷焊的工作环境和工作任务，对机器人进行了参数设计，分析了它的运动学问题和轨迹规划问题。在MATLAB环境下，编制简单的程序语句，对该机器人已规划好的轨迹进行了运动学仿真，验证了参数的合理性，达到了良好的效果。

[1] 叶宏. 玻璃模具的激光合金化处理[J]. 激光杂志, 2000(4)： 48-49.

[2] 蔡自兴. 机器人学[M]. 北京： 清华大学出版社, 2000.

[3] 朱世强. 机器人技术及其应用[M]. 浙江： 浙江大学出版社, 2001.

[4] 陈世健, 张铁. 基于Matlab的喷涂机器人运动学分析[J].机电产品开发与创新, 2008, 21(5)：4-5,18.

[5] 王素玲. BC31环境下DXF图像文件实体数据的提取[J].新乡师范高等专科学校学报, 1999, 13(1)： 113-115.

[6] 樊炳辉. C语言构造DXF图形交换文件的应用[J]. 微型电脑应用, 1998(3)： 86-89.

Study on the simulation of glass mould plasma spray welding robot motion

WANG Qian1, ZHOU Yi-dan1, ZHOU Zi-qiang2, ZHANG Xing-guo1

TP24

A

1009-0134(2011)5(下)-0116-04

10.3969/j.issn.1009-0134.2011.5(下).35

2010-12-18

苏州市科技计划项目：基于工业机器人技术的玻璃模具等离子喷焊加工流水线（ZXG0914）； 江苏省普通高校研究生科研创新计划项目

王倩（1985－），女，江苏徐州人，硕士研究生，研究方向为先进制造工艺及自动加工技术。