大数定律的几个应用

宁小青,刘吉定

(武汉工程大学 理学院，湖北 武汉 430074)

利用概率论思想解决数学分析中的问题，历来受到人们的关注.数学分析中的某些问题如果仅用数学分析的方法来解决，有可能会使问题变得相当复杂，事倍功半.但若适当引入概率论的思想来解决问题或许有意想不到的收获，甚至事半功倍.文献[1-2]给出了几个这方面的结果,下面介绍利用大数定律的其它应用.

为了证明主要结果，先证明两条引理.

引理1 设f(x)与g(x)在[0,b]上有界可积，c>0为常数，f(x)≥0,g(x)≥cx.若n≥2，则 ∀k=1,2,…,n-1，

收敛.

证明因为当0≤x≤b时，有f(x)≥cx，且：

收敛，所以当n≥2时，

收敛.

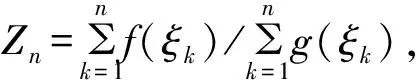
E(Zn2)

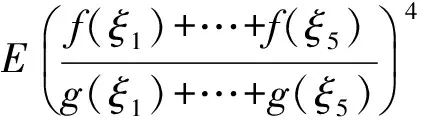
下面给出主要结果及其证明，并利用这一结果证明两个推论.

定理1 设f(x)与g(x)在[0,b]上有界可积，c>0为常数，g(x)≥cx，则：

证明因为f+(x)=max{0,f(x)}，f-(x)=max{0,-f(x)}在[0,b]上有界可积，所以不妨设f(x)≥0.

首先证明：当n∈{5k|k=1,2,…}时，定理1成立.

设ξ1,ξ2,…相互独立，ξi～U[0,b](i=1,2,…).由Kolmogorov强大数定律[4]，知:

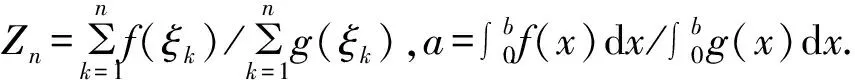
则有:

EZn=E(ZnIAn)+E(ZnIAncB)+E(ZnIAncBc)=E(ZnIAn)+E(ZnIAncB1)+E(ZnIAncBc)+E(ZnIAncB2).

(1)

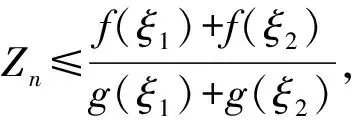
(2)

由P(B1)=0，知E(ZnIAncB1)=0.

(3)

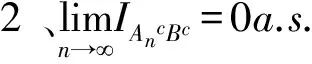
(n→).

(4)

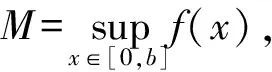
于是：

(E(Zn-5)+3ME(1/(g(ξ6)+…+g(ξn))))P(B).

(5)

由Kolmogorov强大数定律[4]与Lebesgue控制收敛定理[3]，知：

(6)

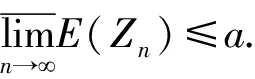
(7)

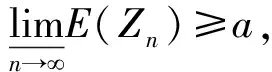
(8)

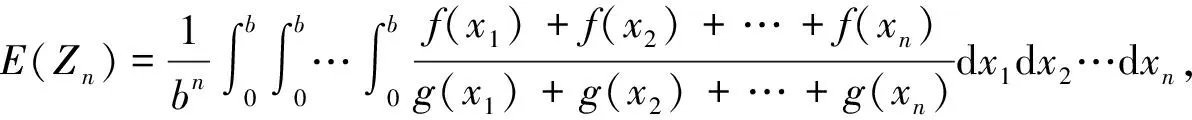
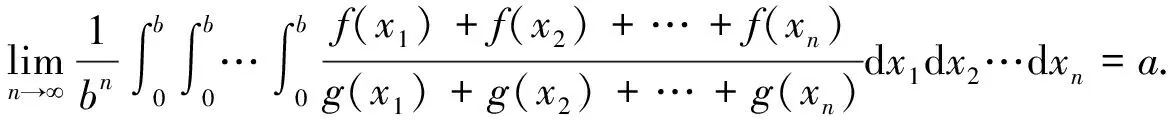
对于其它的n=5k+m,1≤m≤4，根据上述证明，并由：

及式(6)，知：

这就完成了定理1的证明.

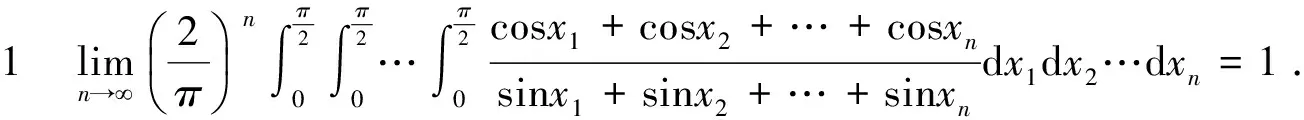
证明由sinx≥(2/π)x(0≤x≤π/2)及定理1，知推论1成立.

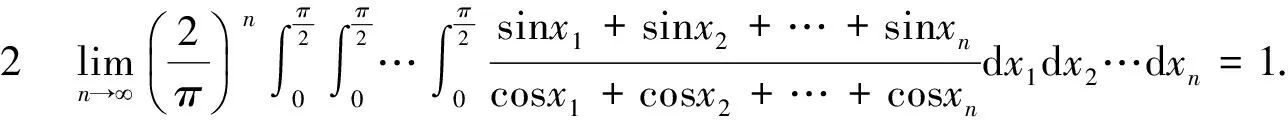
证明令yi=π/2-xi,i=1,2,…,n，并由推论1知推论2成立.

[1] 姚志健.概率论的思想方法在证明数学不等式中的应用[J].甘肃联合大学学报，2009，23(6)：85-88.

[2] 郑淑红.概率论在积分中的应用[J].和田师范专科学校学报，2007，27(5)：16-18.

[3] 严加安.测度论讲义[M].2版.北京：科学出版社，2004:51-68.

[4] 林正炎,陆传荣,苏中根.概率极限理论基础[M].北京：高等教育出版社，2003:95-96.