极限求解中等价无穷小量替换条件的推广

蹇小平

(湖北民族学院 理学院，湖北 恩施 445000)

极限是整个分析学科的工具，极限求解方法众多，其中等价无穷小量代换法求极限是一类重要的切实可行的求解极限的方法，在文献[1-5]中均给出了等价无穷小量求极限的充分条件，受文献[1-8]的启发，本文将上述充分条件进一步推广，从而减弱了利用等价无穷小量替换求极限的条件.

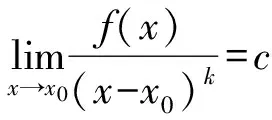
则称f(x)为当x→x0时的k阶无穷小量，记作rx→x0(f(x))=k.

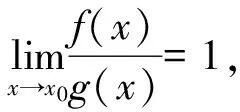
定义3 设f(x)在U(x0)内n阶可导且存在正整数K使得：

f(x0)=f′(x0)=f″(x0)=…=f(k-1)(x0)=0，f(k)(x0)≠0

则称f(x)在x0处满足K阶条件.

例如g(x)=1-cosx则有g(0)=g′(0)=0，g″(0)=1≠0故g(x)满足2阶条件.

关于高阶无穷小量的运算的两个常见结论：

结论1[1-2]xp=ο(xq)(x→0),(p≥q>0)

结论2[1-2]ο(xp)ο(xq)=ο(xq),(p≥q>0)

定理1[1,3,4]若g(x)=ο(f(x))(x→x0) 则有ο(f(x))±ο(g(x))=ο(f(x))，对任给的x∈U°(x0)均成立. 特别地，有ο(xp)±ο(xq)=ο(xp)(x→0)(其中q≥p>0，p,q∈N*)

定理2 设f(x),f0(x);g(x),g0(x);h(x)均为当x→x0时的无穷小量，且f(x)～f0(x)，g(x)～g0(x)，则:

成立的充分必要条件为：

rx→x0(h(x))≤min{rx→x0(f(x)),rx→x0(g(x))}.

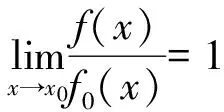
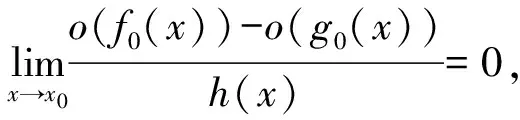
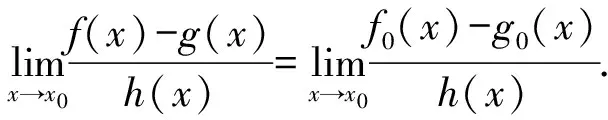
即:

从而由定理1有rx→x0(h(x))≤min{rx→x0(f(x)),rx→x0(g(x))}成立.

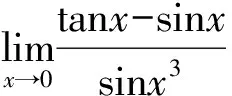
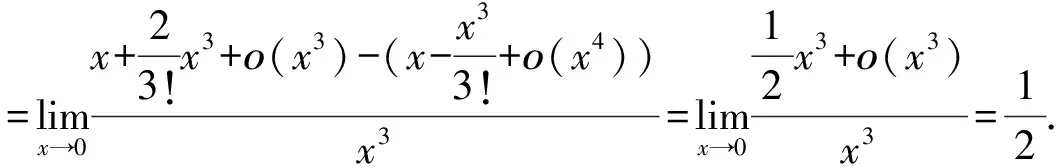
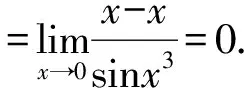
分析因为rx→0(x3)=3>rx→0(tanx)=rx→0(sinx)=1显然不能进行等价无穷小量替换.

下面给出一个等价无穷小量可以进行加减替换的易于判断的充分条件：

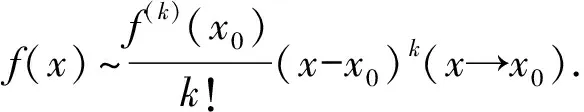
证明由f(x)在U(x0)内n阶可导知：

由f(x)在x0处满足K阶条件，从而有:

于是成立：

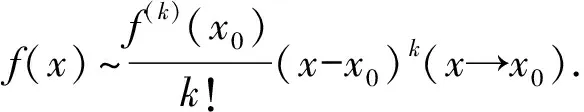
例如g(x)=1-cosx则g(0)=g′(0)=0，g″(0)=1≠0，从而有：

引理2 若f(x),g(x)在x0处满足K阶条件，则：

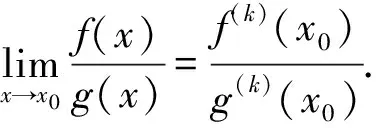
证明由引理1有：

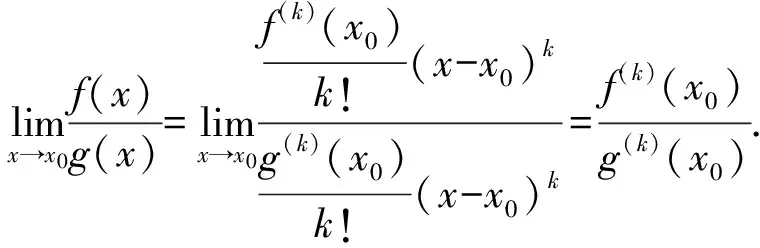
引理3 若f(x)～f0(x)(x→x0) 且在x0处满足K阶条件，则：

f(k)(x0)=f0(k)(x0)

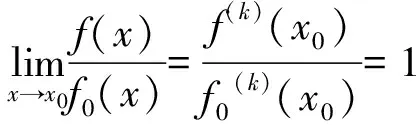
定理3 若f(x)，f0(x)，g(x)，g0(x)及p(x)均在x0处均满足K阶条件，且f(x)～f0(x)，g(x)～g0(x)(x→x0)，则有：

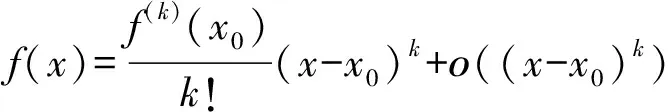
又由引理3得：

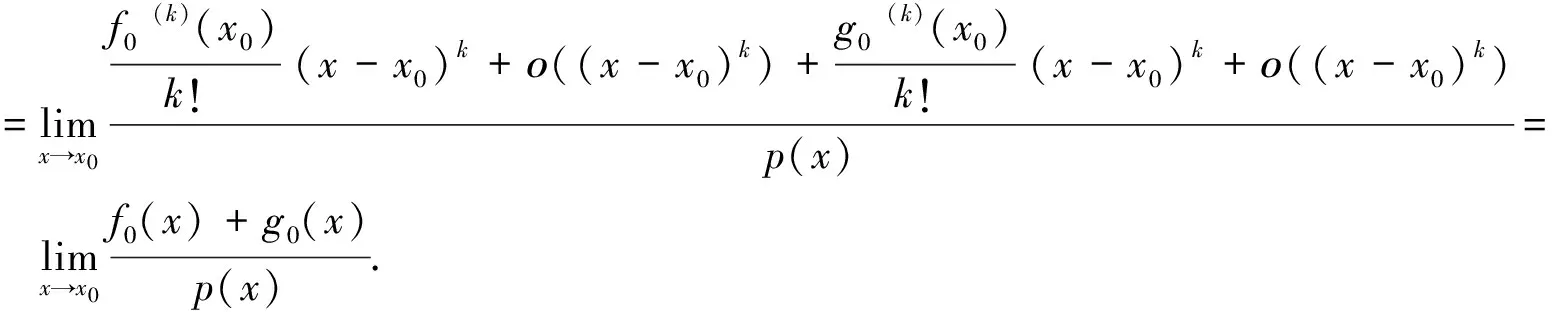
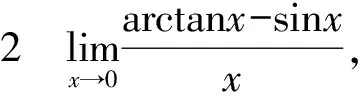
易验证f(x)，g(x)，p(x)在U(0)内满足1阶条件，且有:f0(x)=x～f(x)(x→0)，g0(x)=x～g(x)(x→0) 也满足1阶条件，故:

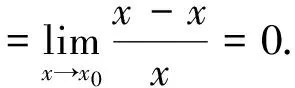
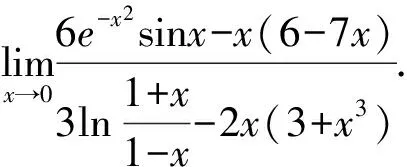
分析若用洛必达法则求解，必须多次求导，且导数越求越复杂，若能正确利用等价无穷小量替换求解却很简单.

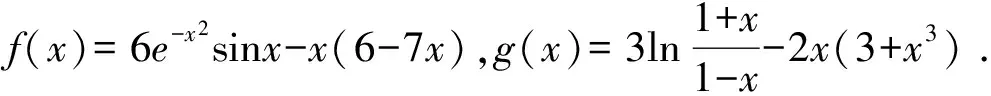
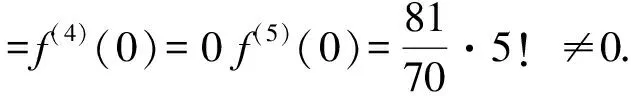
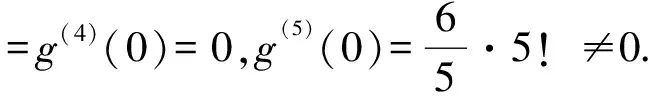
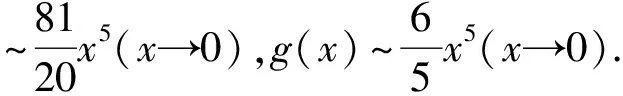
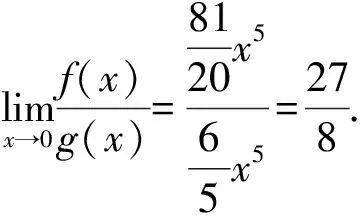
本文的所有结论都是以x→x0的极限过程展开的，事实上本文的结论对于所有极限过程都成立.

[1] 许绍溥.数学分析教程[M].南京：南京大学出版社，2004:60-67.

[2] 陈纪修.数学分析[M].北京：高等教育出版社，2004:100-108.

[3] 刘景麟.微积分[M].北京：国防工业出版社，2006:60-66.

[4] 裴礼文.数学分析中的典型问题与方法[M].北京：高等教育出版社，2001:121-122.

[5] Xiang H L,Qin W J,Liu Z J,et al.Permanence and positive periodic solutions of a difference competitive system with non-linear disturbance[C]// Proceedings of the 7thconference on biological dynamic system and stability of differential equation,Chongqing, P.R. China,May,2010:17-20.

[6] 蹇小平.保谱反乘法映射[J].湖北民族学院学报:自然科学版，2002，16(4):14-16.

[7] 蹇小平.Hilbert空间中几种重要算子[J].湖北民族学院学报:自然科学版，2006，24(1):35-36.

[8] 蹇小平.Euclid空间中几个不等式之新证[J].湖北民族学院学报:自然科学版，2011，29(2):140-142.