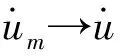
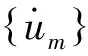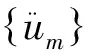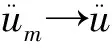一类轴向力与非线性外力混合作用下梁系统的整体解

彭国荣

(湖北民族学院 预科教育学院，湖北 恩施 445000)

1 引言

由杆或梁所组成系统的动力学问题早已成为非线性演化方程领域的一个研究焦点，且已有较多成果.比如J.M.Ball[1]于1973年在一维区间(0,l)上研究了一类非线性屈曲梁:

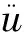
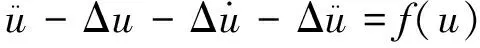
的初边值问题存在全局吸引子.本文在前人基础上考虑非线性外力与轴向力混合作用下粘弹性梁方程在Ω⊂RN上的初边值问题:

(1)

(2)

(3)

其中α>0，β≥0皆为常数，Ω为Rn中一有界凸区域且具有光滑边界∂Ω，‖·‖为通常意义下的L2(Ω)范数，Δ为Laplace算子，为梯度算子，非线性函数f∈C1(R)且满足下列条件：

∀s∈R

(4)

|f′(s)|≤C0(1+|s|p)，∀s∈R

(5)

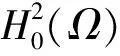
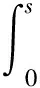
那么，由式(4)可推出，存在正常数λ<λ1及C1,C2满足：

f(s)s≤λs2+C1，∀s∈R

(6)

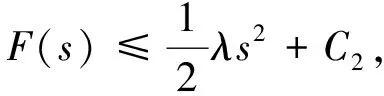
(7)

本文通过Galerkin逼近法，证明了问题整体L解的存在与唯一性.

2 主要结果

u∈L

u满足条件(2)且方程(1) 在L(0,T;L2(Ω))中成立.

3 定理证明

1)构造近似解

设u是Ω上的函数，为简单起见，定义如下的记号：

；

令{ωj(x)}是L2(Ω)一组标准正交向量函数，满足：

Δ2ωj=λj(-Δωj)，

ωj|∂Ω=0，ωj|∂Ω=0，2ωj|∂Ω=0，3ωj|∂Ω=0，j=1，2，…，

λj为与特征函数ωj相对应的第j个特征值，不妨设：

0<λ1<λ2<…<λj<…，λj→(j→)，

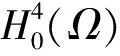
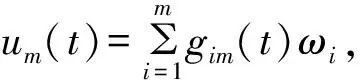
(8)

则对于任意1≤j≤m，um(t)必然还满足：

(9)

且当m→时，令：

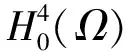
(10)

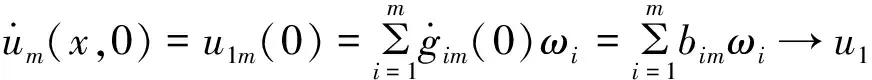
(11)

2)估计

(12)

对上式从0到t积分，记：

可得：

Em(t)≤Em(0).

(13)

据式(7) ，有：

而：

‖um‖2=((-Δ)um,um)≥λ1(um,um)=λ1‖um‖2，

再结合式(12)可得：

(14)

这里C表示一个与m，t无关的正常数，以下C在不同的地方表示不同的正常数且均与m及t无关，不再特别说明.

‖

(15)

由式(10)与式(11)知：‖Δ2um(0)‖，‖Δum(0)‖，‖(0)‖对任意正整数m皆有界.再由f的连续性及式(8)，得：

(16)

由Schwarz不等式，广义Hölder不等式，Sobolev-Poincaré不等式，Gronwall不等式，式(5)、(14)、(15)及(16)有:

(17)

再由Sobolev-Poincaré不等式，有：

‖

(18)

由Lagrange中值定理与Sobolev-Poincaré不等式，结合式(5)知：

‖f(um)‖

(19)

继而有：

‖Δ2um‖，‖Δum‖

(20)

由于上述有界均关于t一致有界，故上述有界性对任意T>0，在t∈(0,T)内成立.

3)收敛性

由上述有界性式(14)至式(20)，知：

{um}在L中有界；

{‖um‖2Δum}在L(0,T;L2(Ω))中有界；

{f(um)}在L(0,T;L2(Ω))中有界；

{um}在H2(Q)中有界.

因为可分赋范线性空间的一致有界线性泛函序列中必可取出一个弱*收敛的子序列，故可选取{um}的子序列，不妨仍记为{um}，再由相关理论，得：

um→u在L中弱*收敛；

‖um‖2Δum→‖u‖2Δu在L(0,T;L2(Ω))中弱*收敛；

f(um)→f(u)在L(0,T;L2(Ω))中弱*收敛；

um→u在H1(Q)中强收敛且几乎处处收敛.

对式(8)两边取L(0,T;L2(Ω))中的极限，有：

成立.

容易证明u满足初始条件及唯一性.

[1] Ball J M.Initial-boundary value problems for an extensible beam [J].Journal of Mathematical Analysis and Applications, 1973, 42: 61-90.

[2] 谢永钦, 钟承奎. 非线性弹性杆中应变孤波的长时间行为的研究[M].兰州：兰州大学,2007.

[3] Silvano D B Menezes, Eliane A de Oliveira,Ducival C Pereira,et al.Existence, uniqueness and uniform decay for the nonlinear beam degenerate equation with weak damping[J]. Applied Mathematics and Computation,2004,154:555-565.

[4] MikhlinS G. Variational Methods in Mathematical Physics[M].Oxford:Pergamon Press,1964.

[5] 杨万必.内积H-Z-空间及其性质[J].湖北民族学院学报：自然科学版，2008，26(4)：383-385.

[6] 谢炜，陈以平，公维凤，等.Banach空间中常微分方程初值问题解的存在性与可解性[J].湖北民族学院学报：自然科学版，2005，23(3)：216-220.

[7] Tokio Matsuyama,Ryo Ikehata.On Global Solutions and Energy Decay for the Wave Equations of Kirchhoff Type with Nonlinear Damping Terms[J].Journal of Mathematical Analysis and Applications,1996,204:729-753.