高效率中点钳位型光伏逆变器拓扑比较

马 琳 孙 凯 Remus Teodorescu 金新民

（1. 北京交通大学电气工程学院 北京 100044 2. 清华大学电力系统及大型发电设备安全控制和仿真国家重点实验室 北京 100084 3. 奥尔堡大学能源技术系 奥尔堡 9220）

1 引言

近年来，分布式发电系统得到了快速的发展。与传统的集中式发电系统相比，分布式发电距离用户更近，发电灵活性更高，能够更充分地利用可再生能源。随着微电网技术的进步，分布式发电系统必将得到更进一步的发展。而光伏并网发电系统正是其中最具典型性的一类，近年来得到了越来越多的关注[1-3]。

图1所示为典型的光伏并网发电系统，主要包括：光伏电池阵列、光伏逆变器、控制器以及储能元件等，其中光伏逆变器是重要的核心部件。光伏阵列产生的低质量直流电，需经过光伏逆变器转换为高质量的交流电传送至电网。太阳能光伏电池板的造价较高，而能量转换效率又较低。因此，为了提高太阳辐射能的利用效率、降低光伏发电的成本，光伏发电系统对于光伏逆变器拓扑的效率有着很高的要求。同时，由于光伏并网发电系统的用户多属于中小型用户，甚至是家庭用户，因此对于光伏发电系统的体积、安装使用的简易程度，以及人身安全性都提出了更高的要求。

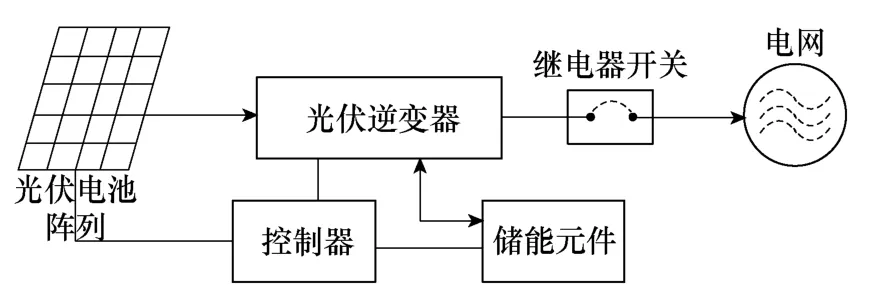
图1 典型的光伏并网发电系统结构Fig.1 Configuration of typical PV generation system

为满足上述需求，近年来研究人员开发了多种无变压器型光伏逆变器拓扑，不仅降低了装置的体积和成本，而且提高了系统的效率和可靠性[4-8]。这些拓扑从原理上来讲可以分为两大类：①H桥改进型拓扑，如H桥直流旁路拓扑[6]、HERIC电路[7]、H5电路[8]等；②三电平中点钳位型（NPC）拓扑，如二极管 NPC[9]、有源 NPC（ANPC）[10-11]、Conergy NPC[12]等。

二极管NPC三电平拓扑最早由A. Nabae等人以论文的方式系统地提出[9]，并已广泛应用于电力传动领域。相对于传统的两电平H桥逆变器，三电平NPC逆变器具有一系列优点：①开关损耗小，效率高。②开关动作时 dv/(dt) 小，引起的电磁干扰（EMI）小。③输出电压波形为三电平，谐波含量少，所需的滤波电感量小，有利于降低系统成本和功率损耗。因此，三电平NPC逆变器非常适用于光伏发电系统。而更为重要的是，当三电平NPC逆变器输入端接光伏阵列时，光伏阵列输出端对地杂散电容上的电压为恒定值，不存在共模电压的问题，即该装置无对地漏电流，避免了对人身的伤害，提高了系统的安全性。

基于上述分析，在未来的光伏发电系统中，三电平NPC拓扑将得到更为广泛的应用。

本文以三种典型的 NPC拓扑（二极管 NPC、有源NPC和Conergy NPC）为研究对象，分析了各自的拓扑结构和调制原理，并采用 MatlabPLECS仿真模块对三种拓扑的功率损耗及分布情况进行了计算。在此基础上，对三种拓扑的性能特点进行了比较分析，并通过实验测试了三种电路的效率。最后，根据比较结果给出了相应的使用建议。

2 二极管NPC调制原理与损耗分析

传统的单相半桥二极管NPC拓扑如图2所示。NPC拓扑的基本工作原理为：当处于正半周期时（参考电压调制信号Sr＞0），在有源供电状态下S1、S2导通，在续流状态下S2、S3同时导通；当处于负半周期时（参考电压调制信号Sr＜0），在有源供电状态下S3、S4导通，在续流状态下S2、S3同时导通。这样的开关状态可以保证在功率因数不为1时，系统仍可正常工作。具体的开关动作如表1和图3所示，表1中“1”代表导通，“0”代表关断。

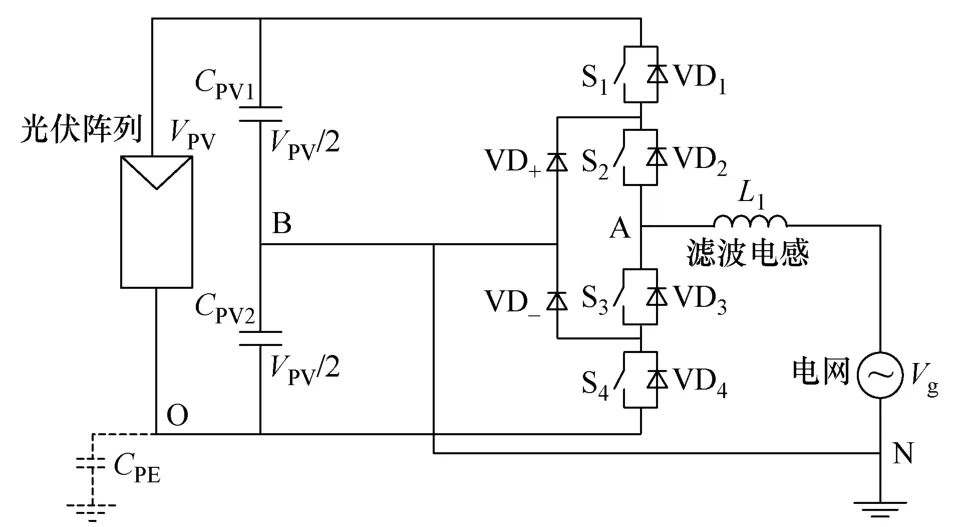
图2 单相半桥二极管NPC拓扑Fig.2 Single-phase half-bridge diode NPC topology

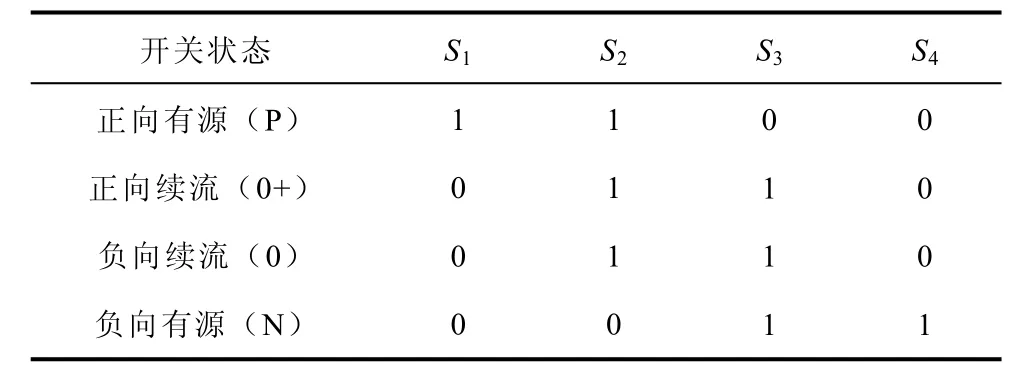
表1 二极管NPC拓扑开关状态表Tab.1 Switching states of diode NPC topology

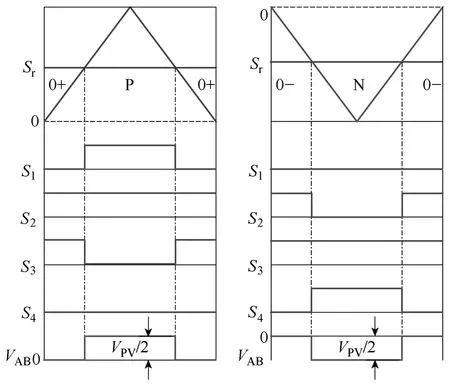
图3 二极管NPC拓扑调制原理Fig.3 Modulation strategy of diode NPC topology

二极管NPC拓扑的两个主要的缺点在于：①在输出电压相同的情况下，输入直流母线电压是传统H桥拓扑的2倍。②开关器件的功率损耗分布不平衡。

一般来说，二极管NPC拓扑的开关器件损耗分布与调制比和功率因数有很大的关系。调制比决定了有源状态和续流状态的比例，理论上高调制比（较低的中间直流电压）可以降低开关损耗。功率因数决定是由反并联二极管承担通态损耗还是由 IGBT承担通态损耗。但调制比和功率因数均是根据外部电源、负载或电网的要求而确定的，在二极管NPC拓扑的运行过程中不能随意调节。因此，一旦电路的输出功率、调制比和功率因数确定后，二极管NPC的功率损耗分布也就确定了，无法调整。

从表1可知，二极管NPC拓扑中内管（S2、S3）不承担高频开关损耗，而外管（S1、S4）承担了几乎所有的开关损耗。因此，在开关频率较高的情况下，即使内管和外管的通态损耗差异不大，两者的总功率损耗也会产生明显的不平衡。而二极管NPC拓扑一般用于大功率电力电子系统。损耗分布不平衡，器件发热不均，使得散热设计困难，影响系统的稳定性和可靠性。这已成为二极管NPC拓扑的一个主要缺点。

为了说明上述问题，本文采用Matlab/Simulink与PLECS模块，对二极管NPC拓扑的开关器件功率损耗进行了仿真计算，如图4所示。仿真中，输出功率为5kW，开关频率16kHz，所用开关器件的型号为PM75DSA120，所有开关器件的结温均固定为 125℃，开关器件总的功率损耗为 35.8W。所有仿真过程中，在测算系统损耗时，为了避免控制所带来的干扰，电网采用纯电阻代替（开环控制）；同时为了保证控制可靠，也进行了并网仿真验证。由仿真结果可以看出，内管（S1）和外管（S2）的开关损耗差别非常大，造成了二者总功率损耗的不平衡。

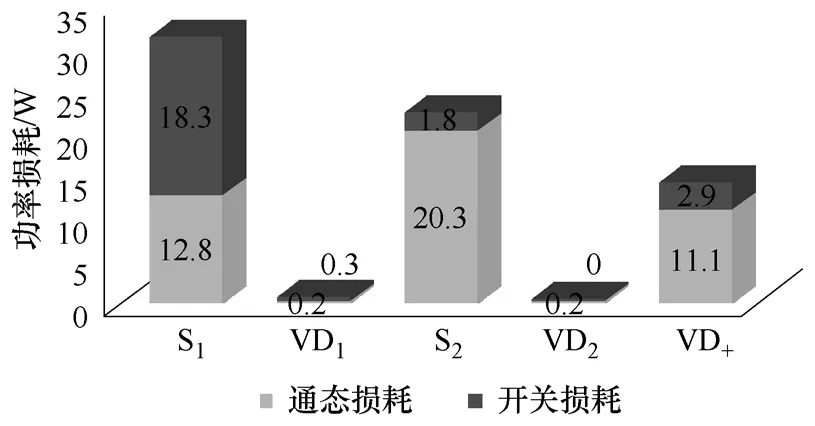
图4 二极管NPC拓扑功率损耗分布Fig.4 Power loss distribution of diode NPC topology

3 有源NPC调制原理与损耗分析

为了解决二极管 NPC拓扑中功率损耗分布不均的问题，文献[10-11]中给出了一种有效的解决方案，即图5所示的有源 NPC（ANPC）拓扑。该拓扑与传统的二极管NPC拓扑相比，具有更多的零续流状态，使得其 PWM调制方式更为灵活。二极管NPC的零续流状态见表1，对于一定流向的续流电流只有一条续流通路。而ANPC则利用两个可控开关器件，将续流回路扩展为两条，大大提高了系统的控制自由度，使得开关器件的功率损耗分布调节成为可能。

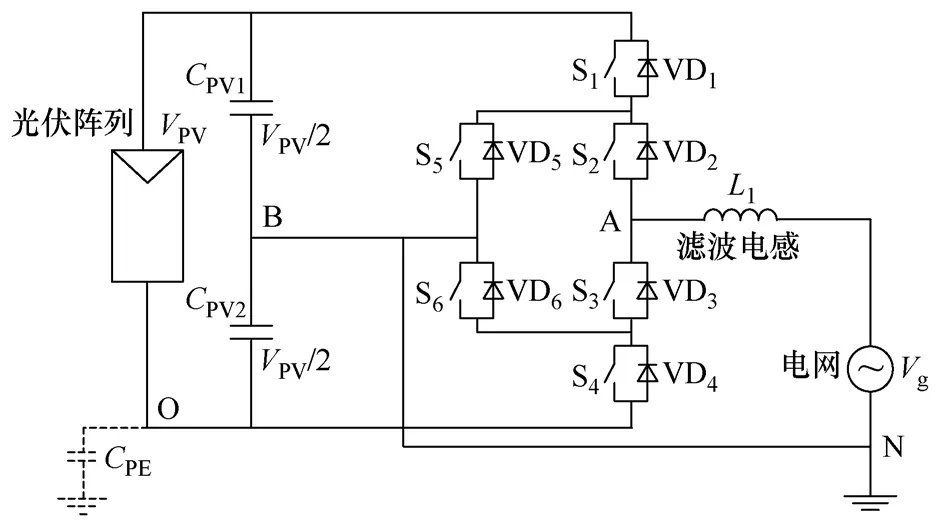
图5 单相半桥ANPC拓扑Fig.5 Single-phase half-bridge ANPC topology

在对 ANPC的控制中，本文采用了一种倍频PWM（DF-PWM）调制方式[12]，其基本原理如表2和图6所示。与传统NPC半桥拓扑采用单极性调制波有所不同的是，在ANPC调制过程中采用的是双极性调制波。

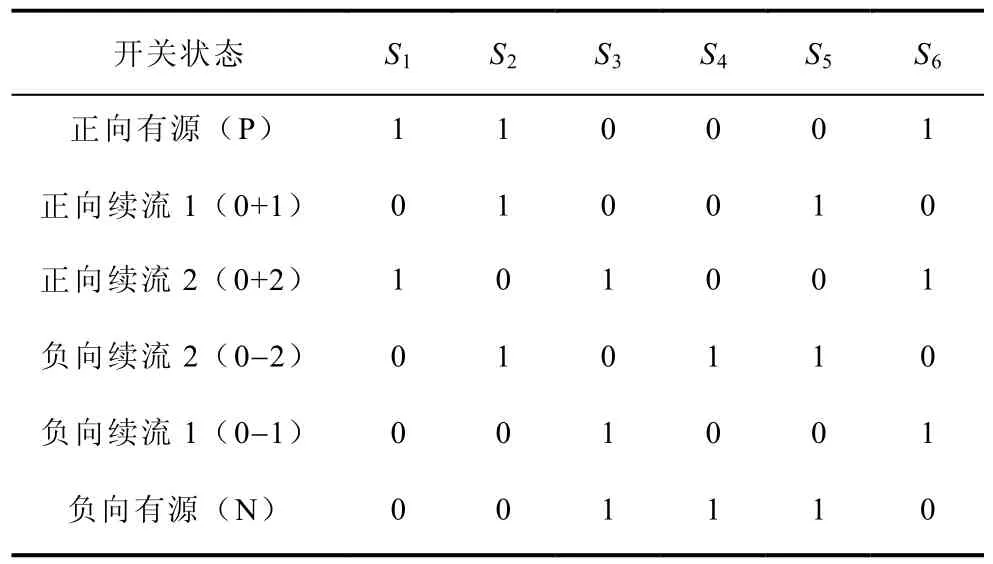
表2 ANPC拓扑开关状态表Tab.2 Switching states of ANPC topology

图6 ANPC拓扑调制原理Fig.6 Modulation strategy of ANPC topology

这种 PWM方式将内管和外管的开关损耗平均分配，以此来实现开关器件总功率损耗的平衡分布。以正半周期为例，从正向续流状态1向正向有源状态换流的过程中，S1、S6导通，S5断开，其中 S5与 S6的动作均属于软开关过程，只有 S1承担了开通损耗；从正向有源状态向正向续流状态2换流过程中，S3导通，S2断开，S2承担了关断损耗，在正向续流状态2下，电流通过S3、S6回路续流；从正向续流状态2向正向有源状态换流的过程中，S2导通、S3断开，其中S3的动作为软开关过程，S2承担了开通损耗；最后，从正向有源状态向正向续流状态1换流，完成一次开关周期的动作，S5导通，S1、S6断开，只有S1承担了关断损耗，在正向续流状态1下，电流通过S2、S5回路续流。从正半周期内一个开关周期的换流过程可以看出，内管和外管各自承担了一半的开关损耗。

为了验证上述分析，本文利用 PLECS模块对ANPC拓扑的功率损耗进行了仿真计算，如图7所示。仿真中，输出功率为 5kW，开关频率 8kHz，所用开关器件的型号为PM75DSA120，所有开关器件的结温均固定为 125℃，开关器件总的功率损耗为135.0W。

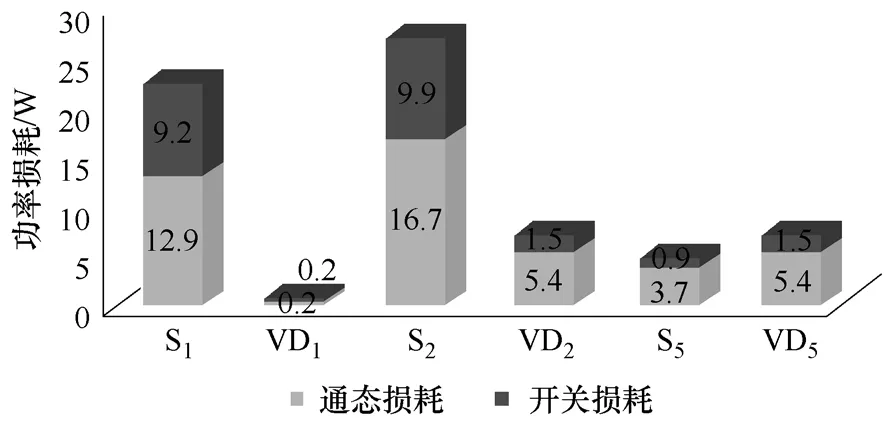
图7 ANPC拓扑功率损耗分布Fig.7 Power loss distribution of ANPC topology

由仿真结果可以看出，内管（S2）和外管（S1）的开关损耗基本上是平均分配的，使得二者总的功率损耗趋于平衡。近来，针对ANPC拓扑研究人员提出了更加灵活的PWM方式[14]。这类方法根据不同的通态损耗情况，适当地改变内管和外管的开关损耗分布，可以实现二者的总功率损耗完全平衡。因此，相对于二极管NPC，ANPC的器件损耗分布能够方便地调节，可解决器件发热不均的问题，有利于大功率应用场合的散热设计。但其缺点在于，比二极管 NPC多用了两个全控开关器件，成本较高，且控制比较复杂。

4 Conergy NPC调制原理与损耗分析

如图8所示，Conergy NPC电路是一种改进型NPC拓扑，它利用一个双向开关（由两个开关器件S+、S-及反并联二极管 VD+、VD-构成）来实现中性点对地钳位的功能。

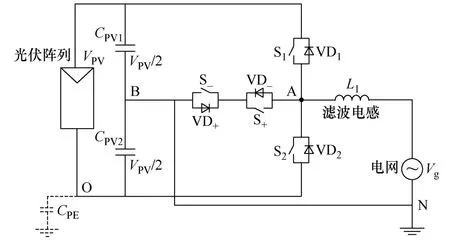
图8 单相半桥 Conergy NPC拓扑Fig.8 Single-phase half-bridge Conergy NPC topology

Conergy NPC拓扑的调制原理如表3和图9所示。以正半周期为例，在有源供电状态下S1导通；在续流状态下S+、S-同时导通，用以保证在功率因数不为1时，电流仍有续流通路。负半周期的调制原理与正半周期类似，在有源供电状态下S2导通；在续流状态下S+、S-同时导通。

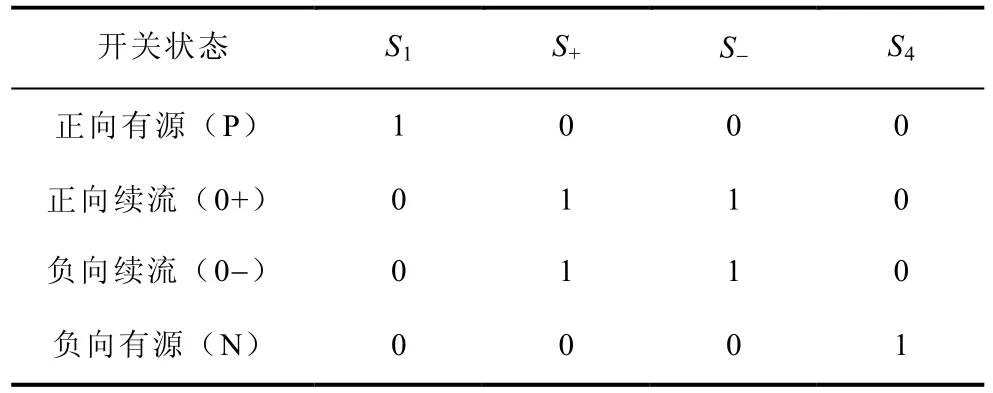
表3 Conergy NPC拓扑开关状态表Tab.3 Switching states of Conergy NPC topology

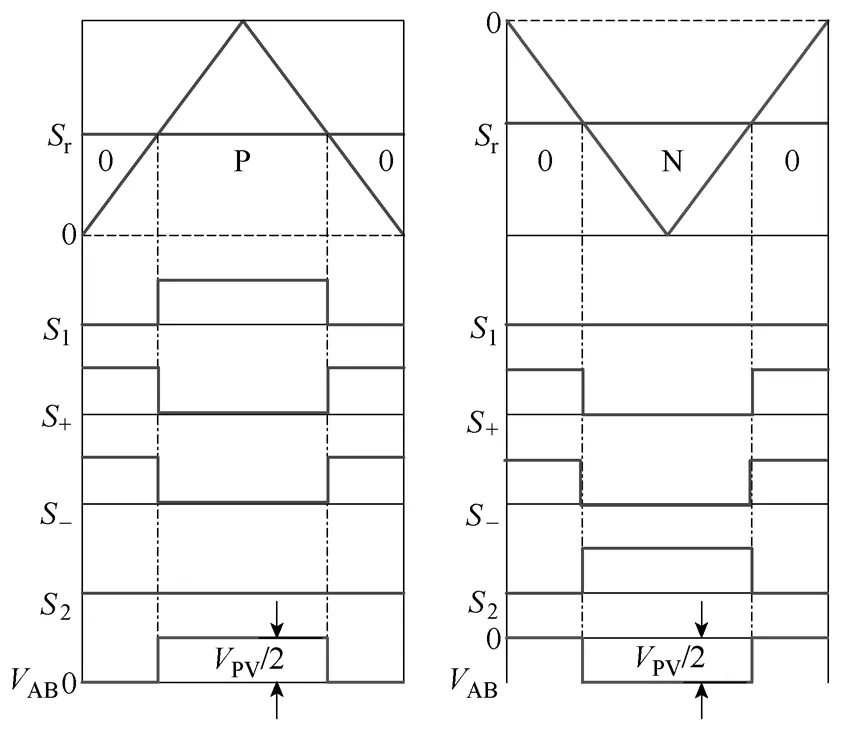
图9 Conergy NPC拓扑调制原理Fig.9 Modulation strategy of Conergy NPC topology

Conergy NPC拓扑具有以下特点：①所用开关器件数目较少，仅用4个IGBT和4个二极管，不仅少于ANPC（6个IGBT，6个二极管），而且少于二极管NPC（4个IGBT，6个二极管）；②不论是正半周期，还是负半周期，续流状态的通态损耗均由S+和S-承担，而同时开关损耗全部由S1、S2承担，这样上下桥臂之间的功率损耗是比较均衡的。

本文利用PLECS模块对Conergy NPC拓扑的功率损耗进行了仿真计算，如图10所示。仿真中设置的参数和器件型号与第2节二极管NPC的仿真完全相同，输出功率为5kW，开关频率16kHz，开关器件的型号为PM75DSA120，所有开关器件的结温均固定为125℃。将图10与图4进行比较可以发现，由于在有源供电状态时，只有一个开关器件导通，因而通态损耗较低，使得该拓扑的总功率损耗低于二极管NPC，其效率更高。

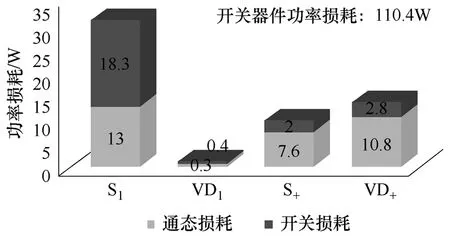
图10 Conergy NPC拓扑功率损耗分布Fig.10 Power loss distribution of Conergy NPC topology

5 三种NPC半桥拓扑的比较

实际上，上文所介绍的所有拓扑均为半桥拓扑，而 NPC半桥拓扑与所有的半桥拓扑一样具有电压利用率低（仅为全桥拓扑的一半）、电压电平数量少的缺点。但是，由于NPC半桥拓扑可以直接将其中性点接地，消除共模电压干扰，因此在光伏并网领域得到了广泛的应用。与传统半桥电路相比，NPC半桥电路最大的优势在于具有三电平（传统半桥电路只有两电平），同时可以直接运用到交流逆变系统中，因此NPC半桥电路成为了一种广泛应用于光伏逆变器的拓扑。

为了探索高效率、高性能且经济适用的光伏逆变器解决方案，本文对上述三种NPC拓扑的器件数目和能量转换效率进行了比较。

三种拓扑所用的器件数目见表 4。从表 4中可以看出，如果选择相同型号的 IGBT和二极管构成主回路，则Conergy NPC的器件成本最低，二极管NPC次之，而ANPC的器件成本最高。

表4 NPC拓扑器件数目比较Tab.4 Comparison of the device number used in NPC topologies

本文在相同的单相 NPC实验平台上对上述三种拓扑在不同输出功率下的主电路效率进行了实验测试，实验参数见表 5。为了更加公正地比较电路效率，实验采用开环给定调制比的控制方法，输出电压经过纯电感滤波器后接电阻作为负载。这样在比较过程中就消除了不同的控制及电网对逆变器的影响。

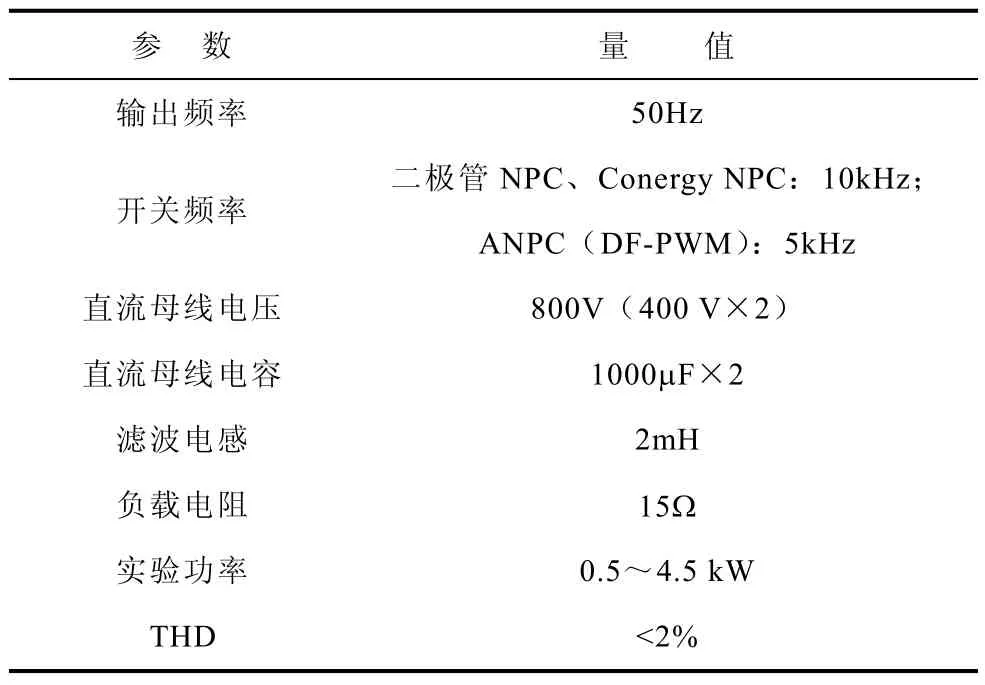
表5 NPC拓扑实验参数Tab.5 Parameters in NPC topology experiments

从图3、6、9中可以发现，在一个开关周期内ANPC的开关次数是二极管NPC和Conergy NPC的两倍。因此，为了准确地比较开关损耗，在实验测试中二极管 NPC和 Conergy NPC的开关频率为10kHz，而ANPC（DF-PWM）的开关频率为5kHz。

开关器件采用三菱智能功率模块（IPM），型号为PM75DSA120。每个模块均采用隔离光纤信号驱动，并自带过电流保护功能，并采用铜排连接，结构简单，易于调整拓扑。图 11为进行 ANPC实验时的平台。由于实验输出波形类似，在本文中仅给出调制方法最为复杂的ANPC拓扑的实验波形，其他波形不再赘述。

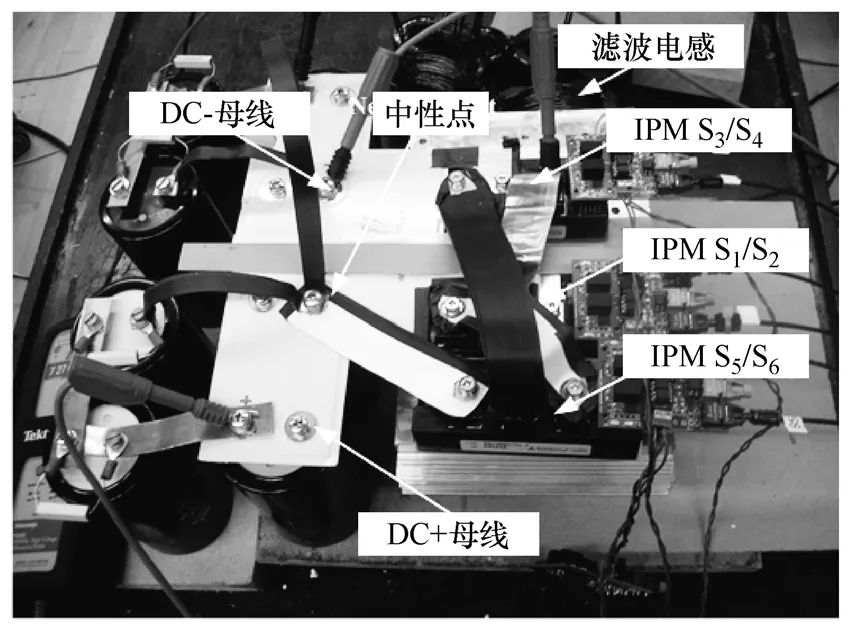
图11 ANPC实验平台照片Fig.11 Photo of ANPC experimental setup

图12为ANPC的实验波形，其中Ch2为输出电流，其他通道为相应的IPM驱动信号。

三种拓扑的效率对比曲线如图13所示。从实验结果可以看出，在采用相同开关器件的条件下，Conergy NPC的效率最高，而ANPC与二极管NPC的效率非常接近。三者的效率均是随着输出功率的增大而提高，且效率最高值均可以达到97%以上。

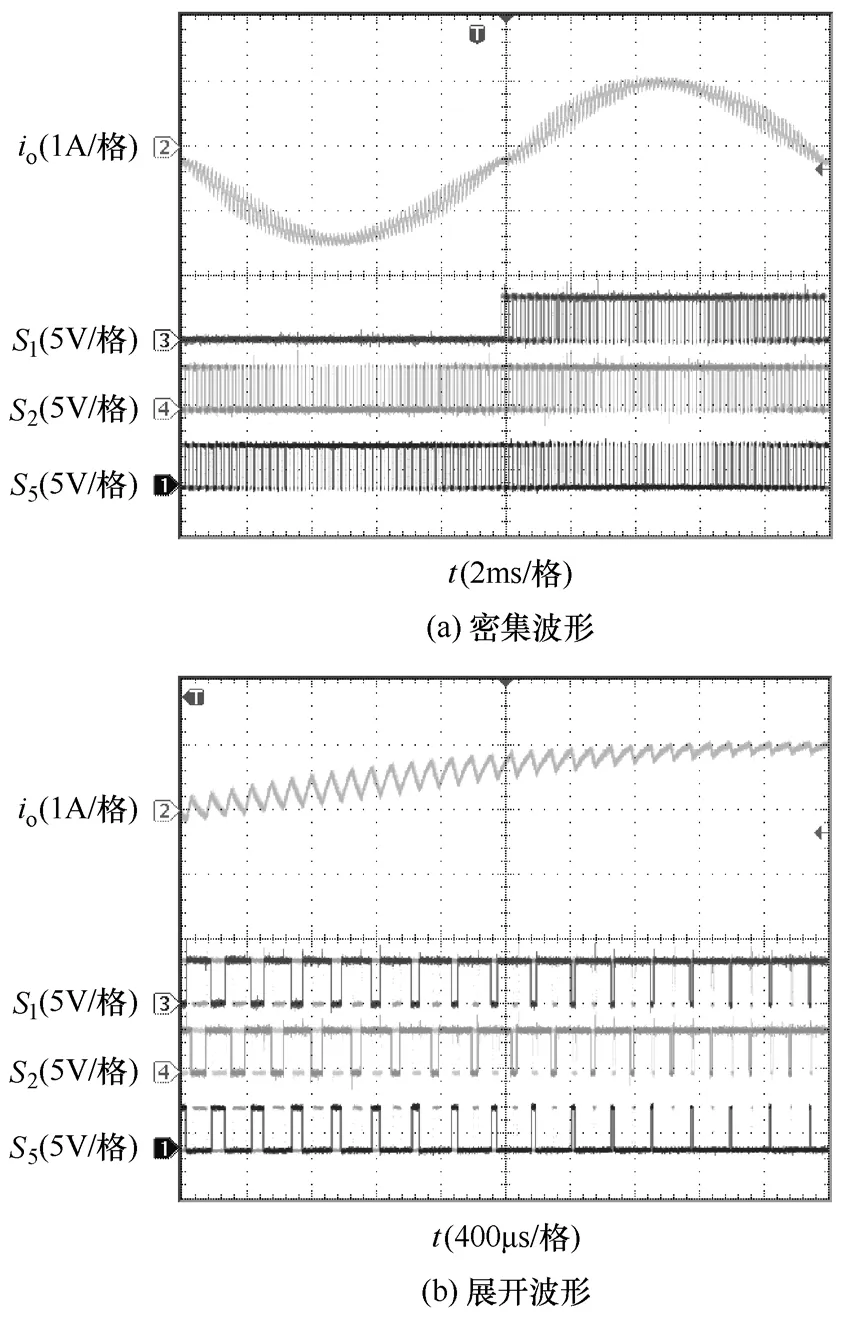
图12 ANPC实验波形Fig.12 Experimental results of ANPC

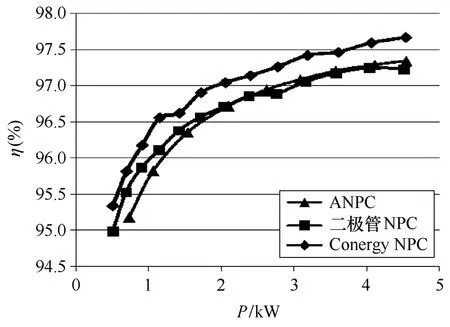
图13 NPC拓扑效率比较Fig.13 Comparison of the efficiency for NPC topologies

6 结论

本文以光伏逆变器为应用背景，深入地研究了NPC拓扑的结构特点和工作原理。对三种典型的单相半桥NPC拓扑（二极管NPC、ANPC和Conergy NPC）的器件成本、调制方式、损耗分布以及效率进行了比较分析。研究结果表明：

（1）Conergy NPC的效率在三种拓扑中最高，且在使用相同开关器件的条件下其器件成本最低。

（2）ANPC的功率损耗分布可以灵活调节，有利于大功率应用场合的散热设计，但其控制比较复杂，且器件成本在三种拓扑中最高。

（3）二极管 NPC拓扑的功率损耗分布不易调节，不利于大功率应用场合的散热设计。

综上，Conergy NPC是一种高性能、高效率且经济适用的电路拓扑，应在未来光伏逆变器的开发中得到更为广泛的应用。

[1] 刘飞, 查晓明, 周彦, 等. 基于极点配置与重复控制相结合的三相光伏发电系统的并网策略[J]. 电工技术学报，2008，23(12)：130-136.Liu Fei, Zha Xiaoming, Zhou Yan, et al. Research on grid-connected strategy combining pole-assignment and repetitive control in three-phase photovoltaic system [J]. Transactions of China Electrotechnical Society, 2008，23(12)：130-136.

[2] 杨水涛，张帆，丁新平，等. 基于输入-输出参数的光伏电池最大功率控制的比较[J]. 电工技术学报，2009，24(6)：95-102.Yang Shuitao, Zhang Fan, Ding Xinping, et al.Comprehensive research on the photovoltaic maximum power point tracking based on input parameters or output parameters [J]. Transactions of China Electrotechnical Society, 2009, 24(6)：95-102.

[3] 周德佳，赵争鸣，袁立强，等. 300kW光伏并网系统优化控制与稳定性分析[J]. 电工技术学报，2008，23(11)：116-122.Zhou Dejia, Zhao Zhengming, Yuan Liqiang, et al.Optimum control and stability analysis for a 300kW photovoltaic grid-connected system [J]. Transactions of China Electrotechnical Society, 2008, 23(11)：116-122.

[4] Ma Lin, Kerekes T, Teodorescu R, et al. The high efficiency transformer-less PV inverter topologies derived from NPC topology[C]. Proceedings of EPE2009, 2009: 1 -10.

[5] Kjær S, Pedersen J, Blaabjerg F. A review of single-phase grid connected inverters for photovoltaic modules[J]. IEEE Transactions on Industry Applications, 2005, 41(5): 1292-1306.

[6] Gonzalez R, Lopez J, Sanchis P, et al. Transformerless inverter for single-phase photovoltaic systems[J].IEEE Transactions on Power Electronics, 2007, 22(2):693-697.

[7] Schmidt Heribert. European, 03009882.6[P]. 2003-05-15.

[8] Matthias Victor. United States, US2005/0286281 A1[P]. 2005-12-29.

[9] Nabae A, Takahashi I, Akagi H. A new neutralpoint-clamped PWM inverter[J]. IEEE Transactions on Industry Application, 1981, 17: 518-523.

[10] Floricau D, Floricau E, Dumitrescu M. Natural doubling of the apparent switching frequency using three-level ANPC Converter[C]. International School on Nonsinusoidal currents and Compensation, 2008:1-6.

[11] Brückner T, Bernet S, Steimer P K. The active NPC converter for medium-voltage applications[C].Proceedings of IEEE IAS, 2005, 1: 84-91.

[12] Knaup P. WO 2007/048420 A1[P]. 2007-05-03.

[13] Bruckner T, Bernet S, Guldner H. The active NPC converter and its loss-balancing control [J]. IEEE Transactions on Industrial Electronics, 52(3):855-868.

[14] Ma Lin, Jin Xinmin, Kerekes Tamas, et al. The PWM strategies of grid-connected distributed generation active NPC inverters[C]. IEEE Energy Conversion Congress and Exposition, 2009: 920-927.