编组站车流接续优化模型及算法

甘志雄，何世伟，申永生，黎浩东，程金星

（北京交通大学 交通运输学院，北京 100044）

编组站车流接续优化模型及算法

甘志雄，何世伟，申永生，黎浩东，程金星

（北京交通大学 交通运输学院，北京 100044）

在解编顺序给定的条件下，建立车流接续优化模型。在模型构建中，列车属性方面同时考虑了换重、换长和满轴三个约束，通过算例证明，该设定不但更加符合实际，而且使得车流接续优化具有了一定的灵活性。在算例分析部分，分别利用一般数学软件Lingo11.0以及VC++编写的自适应免疫克隆算法对模型进行求解，证明了模型和算法的有效性，为编组站阶段计划车流接续优化智能化提供了较好的解决途径。

编组站；调度计划；车流接续优化；自适应免疫克隆算法；Lingo

1 引言

编组站作为运输网络中的重要结点，担负着列车的到、解、集、编、发等任务。货运过程中的大部分时间是消耗在编组站内，这当中很大一部分时间是由于设备不足或是技术作业组织不够合理而导致的等待时间。而有效的、合理的编组站调度优化方式能够使列车在技术作业过程中以最少的时间，完成最多的货车周转，使得编组站在有限的作业设备基础上达到运输效率最大化。

车流接续优化作为编组站调度优化中的一个主要构成部分，是编组站调度计划优劣的重要评估标准。车流接续优化效果的好坏，直接影响着到达车组给出发列车提供车流来源合理性，从而影响到车组在站停留时间、出发列车编组内容以及出发列车是否能准时出发，对车站和整个路网的车流周转时间有着决定性的作用。提升车流接续优化效果，对提高编组站和整个路网的效率都有很大的帮助。

许多学者对问题进行了研究。文献[1]利用表上作业法对车流接续优化进行求解，效果比较理想，但是在求解大规模问题时，求解的时间会大幅度增长。文献[2]提出以列车配流为主线，通过构造局部区域优化问题实现解体、编组方案优化的启发式算法，但其算例结果有待商榷。文献[3]对编组站车流接续进行了动态配流研究，并给出了模型和相应的算法，但是列车属性方面只考虑了满轴数。文献[4]对基于解编顺序的车流接续优化模型及算法进行研究，但是列车属性方面只考虑了车辆满轴数。文献[5]以调机活动为核心，结合文献[1]提出的静态车流推算方法，建立以出发列车尽可能满轴为目标的数学模型，设计了求解该模型的混合遗传算法，但文中给出的算例结果不太理想，同时算法的时间效率不高。文献[6]根据编组站实际作业流程，将阶段计划自动编制问题分解为配流计划、解体／编组计划、到发线运用计划3个自动编制子问题，分别建立数学模型并求解。

当前对于车流接续优化的研究，出发列车属性一般只考虑出发列车车辆数满轴。本文结合实际生产需要，同时考虑了列车的换重、换长和满轴数三个约束并建立数学模型，分别利用一般数学软件Lingo11.0和自适应免疫克隆算法对模型进行了求解。

2 数学模型

2.1 符号定义

设编组站本阶段到达列车m列，其中计划开始阶段的站存车和货场而来的车均视为到达车数，出发列车n列，F为编组站车组方向编号的数量，f为编组站车组方向编号，f=1，…, F，Tk为车组k所在到达列车到达时刻，Ak为车组k所含车辆数，DTj为出发列车j的出发时刻，Lk为车组k的换长，Wk为车组k的换重为出发列车Dj允许的最小换长，为出发列车Dj允许的最大换长，为出发列车Dj允许的最小换重，为列车Dj允许的最大换重为出发列车Dj允许的最小车组数，为出发列车允许的最大车组数，N（j）表示在满足车流接续时间约束下，能够为出发列车Dj提供车流的到达车组集合。M为大的正整数，为了保证约束的可行性，Xjk表示车组k为Dj提供车流的车辆数，为0-1变量1表示出发列车满足换重要求，为0-1变量=1表示出发列车满足换长要求为0-1变量，=1表示出发列车满足车组数要求。

2.2 模型构建

在列车属性方面同时考虑出发列车换重、换长和满轴数的基础上，以车组在站停留时间最短为目标，建立目标函数：

约束（2）表示到达车组k或是作为出发列车的车流来源，或是最终成为下一阶段计划开始时的站存车。约束（3）表示出发列车换重小于最大规定换重量，约束（4）表示若出发列车换重大于最小的换重要求，则=1。约束（5）表示出发列车换长必须要小于最大规定换长，约束（6）表示若出发列车换长大于最小的换长要求，则=1。约束（7）表示出发列车车组数量必须要小于最大规定车组数，约束（8）表示若车组数之和大于最小的规定车组数要求，则=1。约束（9）表示出发列车在换重、换长和满轴这三个约束中只需满足其中一个。

3 模型求解

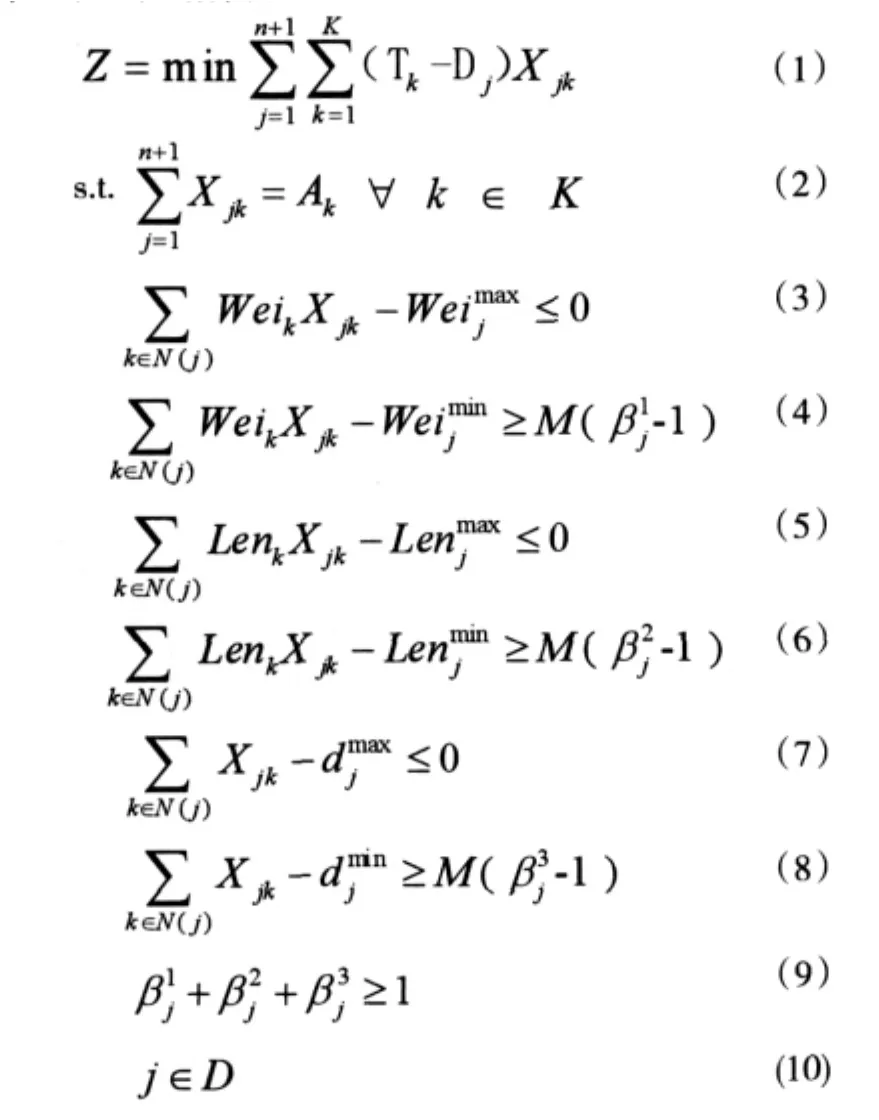
在求解车流接续优化问题上，表上作业法和一般的数学软件都能够求解。一般的数学软件在求解小规模线性问题时往往能比较快的获取到全局最优解，但是在处理非线性大规模问题时，求解效率上往往无法使人满意，随着规模的增大，求解时间呈指数增长。而智能算法在求解非线性大规模问题相比于一般的数学软件往往有比较大的优势。

在诸多智能算法中，免疫算法具有克隆、超变异、抗体与抗原特异性结合、未被激发的细胞消亡及记忆细胞的产生等特色,因此在保证收敛速度的同时又能维持抗体的多样性，为目标优化提供了一种有效的新途径，近几年引起了研究者更多的关注。考虑到免疫算法的诸多优点，现采用其作为VC6.0中优化解编顺序的智能算法。文献[7]提出的算法是近年来提出的比较典型的一种克隆选择算法。在免疫诸多算法的基础上，文献[4]进一步提出了自适应克隆选择算法。本文所实现的免疫算法为自适应克隆选择算法（Adaptive Colonel Select Algorism，简称ACSA），借鉴了文献[4]提出的自适应克隆选择理论。下面给出该算法设计和实现的详细说明。

3.1 ACSA设计说明

（1）抗体（解）的表示：以整数编码组成抗体，抗体长度为到达列车车组个数K。抗体的编码为每个到达车组满足时间接续和空间接续条件下的出发列车编号。

（2）适应度计算：通过解析每个抗体个体中能满足出发要求的出发列车数来确定适应度。需特别说明的是，由于智能算法存在着初始解的随机生成以及变异的随机性，可能导致无效抗体的产生，比如抗体解析结果无法满足时间约束，算法对无效抗体的适应度赋予值-1，从而使该抗体适应度值很低，在克隆过程中由于其亲和度很低导致该抗体克隆个数很少，在克隆群体中的比例很小，选择其进入新群体的可能性很低，最终这些抗体或消亡，或通过变异以新的较优解的形式存在于新群体中。

（3）克隆个数的确定：设定克隆个数最大值cnMax和克隆个数最小值cnMin。每个抗体具体的克隆数cn与其亲和度成正比，本文设计的关系为cn=cnMax（1-i/N）,cn＞=cnMin，其中N为抗体群体规模，将要克隆的抗体按亲和度大小排序，i是其序号。从上述关系式中可以看出，亲和度越大的，其克隆数量越多，这是自适应的一个特点所在。

（4）变异概率的确定：进化初期，为了保证抗体群的全局搜索，需要一个较大的变异概率，随着进化代数的增加，抗体群适应度相应也会提高，此时变异概率需要变小以便算法收敛。设置变异概率φ为迭代步骤m的函数，其关系式为φ=ρ·（M-m）/M，其中ρ为变异概率常数，M为迭代步骤的最大值。

（5）选择个数的确定：克隆选择算法里要求选择个数d反比于群体适应度，设定d为迭代步骤m的函数，其关系式为d=θ·（M-m）/M，其中θ为选择常数，M为迭代步骤的最大值。从该关系式中可以看出，随着迭代步骤的增加，抗体群适应度越高，选择的个数会越来越少，从而抗体群会越来越稳定收敛于一点，这是自适应的第二个特点所在。

（6）算法运行的终止条件为当最优值连续迭代5次不再变化或者迭代次数达到迭代最大步骤M时，即代表了算法已经收敛到最优解，可以终止运行，输出最优值。

3.2 利用自适应免疫克隆算法求解优化模型实现步骤

Step.1：读取到达列车和出发列车的信息：包括到达列车的到达时刻，编组方向及车组数量；出发列车出发时刻，编组去向，以及各个车组的换长、换重和车组数要求。

Step.2：确定解编顺序。

Step.3：基于到达列车的解体顺序，考虑单调机资源约束，求解每个到达列车的解体时刻。

Step.4：基于出发列车的编组顺序，考虑单调机资源约束，求解每个出发列车的编组时刻。需要说明的是，当某个出发列车编组时刻要晚于出发列车的最晚编组时刻，则说明该列车无法在该阶段作业时间内准时编组出发，本文对于此类列车的车流接续策略为优先为其它出发列车车流接续。

Step.5：各个到达车组的解体时刻以及各个出发列车的编组时刻确定后，结合编组去向，确定每个到达车组可接续的出发列车序号集合D。

Step.6：根据Step.4的结果，初始化群体P。以整数编码组成抗体，抗体的长度为到达列车车组个数K。抗体的编码为集合D中随机获取的一位。

Step.7：调整群体P中每个抗体。调整策略为：对于初始群体中的某个抗体，首先计算出各个出发列车的车组情况，如果该出发列车满足上文所提到的换重、换长或满轴数要求，则不进行调整；如果某个出发列车车流接续情况超过了换长的上限或是换重的上限或是车组数量的上限，则把为该出发列车提供车组的到达车组数量进行减除调整，直到该出发列车满足换重换长和满足车组数上限要求，把减除的整个车组或车组中的某些车放入站存车集合中。在减除调整完成后，进行某些出发列车增轴调整：把不满足换重、换长或满轴数下限的出发列车进行增加调整，从站存车集合中获取满足该出发列车接续的车组进行补充，直到满足要求。如果没有满足列车接续的车组，则不进行增加。通过上面的调整可以获取到每个抗体车流接续的初始化编码，每个编码出发列车正点出发的列车数量作为适应度函数大小的评定标准。

Step.8:克隆。对抗体群P中的抗体进行克隆扩增操作，得到扩增后的抗体群C，每个抗体克隆数按照算法设计说明的第（3）点自适应确定。

Step.9：高频变异。对抗体群C中的抗体进行高频变异，得到C*。变异概率按照算法设计说明的第（4）点自适应确定。

Step.10：选择。从C*中选择d个适应度高的抗体替换P中d个低亲和度抗体。d按照算法设计说明中的第（5）点自适应确定。

Step.11：判断终止条件是否满足，如果未满足则转至Step.7。

Step.12：如果终止条件满足，则程序结束，输出最优解。

4 算例分析

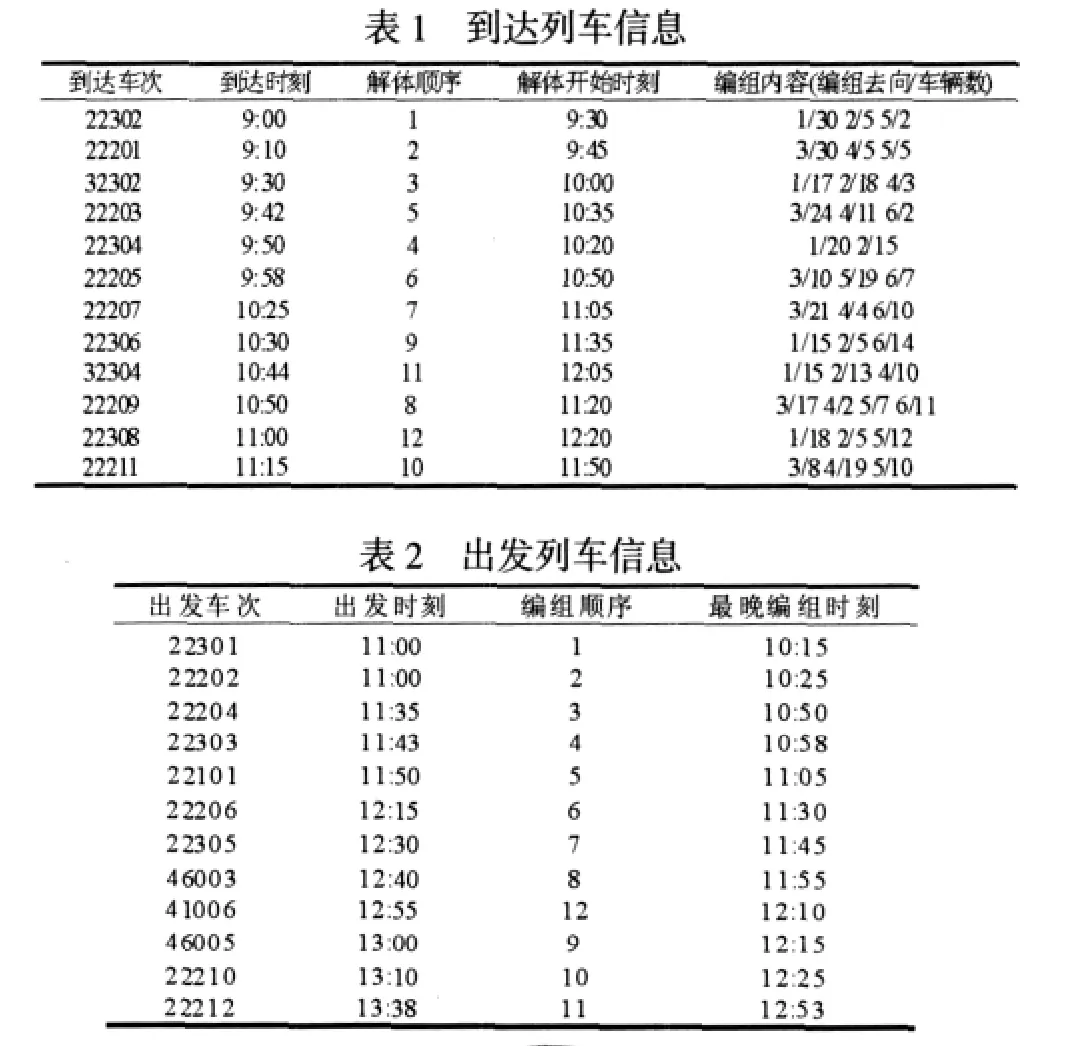
算例中到达列车和出发列车信息见表1和表2，该原始数据来自文献[2]。解体次序代表着该到达列车在该阶段的解体次序，解体开始时刻代表着该列车解体作业的起始时间。编组顺序代表着该列车在该阶段的编组次序，最晚编组时刻代表着该列车的由于计划出发时刻和技术作业所需要的时间，必须在此时刻开始编组，否则将会晚点。本文中令出发列车的满轴数为35，换长区间为[37,44]，换重区间为[36,43]。即出发列车满轴数为35，最小换长要求为37，最大换长为44，最小换重为36，最大换重为43。为了证明前面提到的一般数学软件和自适应免疫算法在求解这类问题上的不同表现，本算例分别使用Lingo11.0和自适应免疫克隆算法进行求解。

4.1 Lingo11.0求解车流接续优化模型

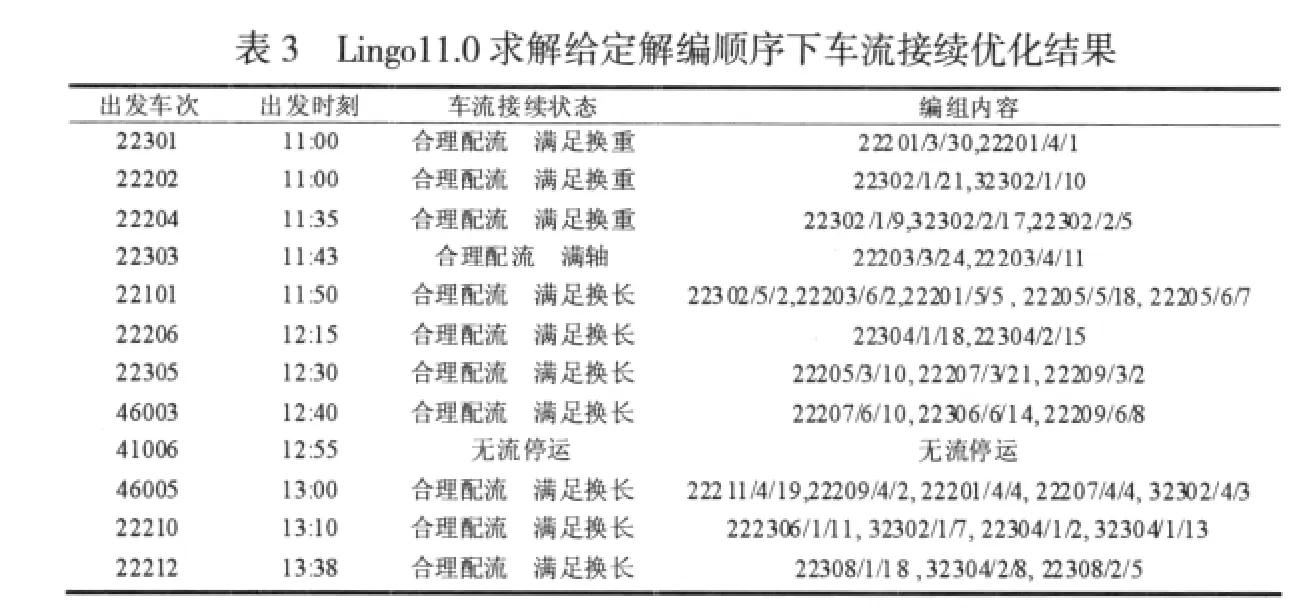
本文在出发列车同时考虑换长、换重和满轴数约束的基础上，以车组在站停留最短为目标函数，通过Lingo11.0进行求解。求解结果见表3。

4.2 自适应免疫克隆算法求解车流接续优化模型

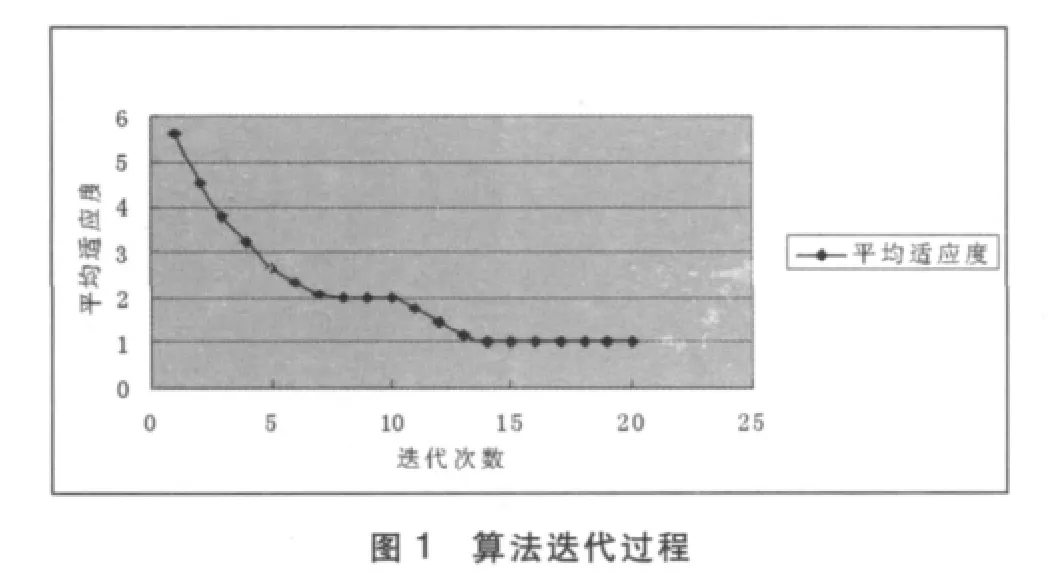
通过实现文中提出的自适应克隆选择算法求解，在抗体规模和变异概率φ、选择常数θ、最大克隆数和最小克隆数取不同数值的条件下，对算法进行了多次测试，结果表明，当抗体规模在20-30范围内变化、变异概率φ在0.5-0.8范围内变化、最大克隆数在15-10范围内变化、最小克隆数在5-3范围内变化时，算法均可收敛至相同的最优解，说明对参数的依赖性不强，有较好的稳定性。算例实现的参数设置如下：抗体规模为20，变异概率常数φ取值0.6，选择常数θ取值为5。最大克隆数为10，最小克隆数为3，迭代代数为20。算法迭代过程如图1所示，迭代总次数为20次，当迭代到14次后，群体平均适应度就收敛到1。求解结果见表4。

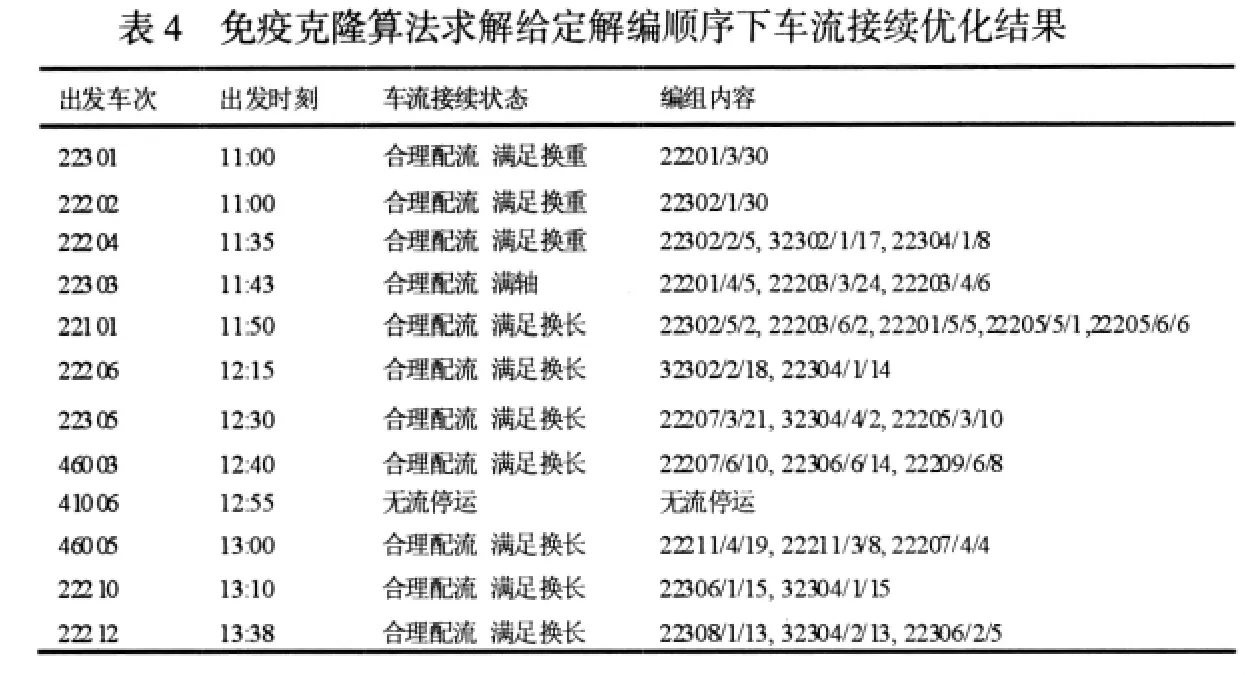
4.3 算例结果分析

通过对车流接续优化模型的实例分析可知，Lingo11.0和自适应免疫克隆算法都能很好的求解车流接续优化，而且效果都不错。在求解小规模线性规划问题中，Lingo11.0相比于自适应免疫克隆算法无论在求解的时间或是求解效果上都要好， Lingo11.0有以下几个优势：（1）其编程建立于建模语言基础上，语句最简单易懂；（2）在小规模线性问题上求解时间短，Lingo11.0通过13秒就可以获得全局最优解，自适应免疫克隆算法迭代过程用了16秒左右；（3）求解效果好，易收敛于全局最优解。

在本算例中可以发现，Lingo11.0求解的结果是全局最优解，要好于自适应免疫克隆算法求解的结果：在正点出发列车数相等的情况下，自适应免疫克隆算法求解的车流接续优化结果车组停留时间较多。但是当车组数增加后，Lingo 11.0求解所需的时间呈指数增长，而免疫克隆算法迭代的时间增加是可控的。

5 结论

本文建立了在解编顺序给定下的车流接续优化模型，并用一般的数学软件和自适应免疫克隆算法进行了求解，结合算例，证明了模型和算法的合理性。

列车属性方面同时考虑了换重、换长和满轴数三个约束，通过算例证明，相比于列车属性只考虑满轴正点出发，该设定不但更加结合实际生产，而且使得车流接续优化具有了一定的灵活性。

自适应免疫克隆算法在求解车流接续优化大规模问题时比Lingo求解的效率要高，但是往往获得的不是全局最优解。而Lingo获得的是全局最优解，在处理小规模线性问题时，效果比智能算法要好。

[1]王慈光.用表上作业法求解编组站配流问题的研究[J].铁道学报，2002，24（4）：1-5.

[2]王明慧，赵强.编组站智能调度系统阶段计划优化模型及算法研究[J].铁道学报,2005，27（6）：1-9.

[3]王慈光.编组站动态配流模型与算法研究[J].铁道学报，2004，26（1）：1-6.

[4]申永生，何世伟，王保华，穆美如.免疫算法求解编组站阶段计划配流问题研究[J].铁道学报，2009，44（4）：1-6.

[5]王正彬，杜文，吴柏青，羊艳.基于解编顺序的阶段计划车流推算模型及算法 [J].西南交通大学学报，2008，43（1）：91-95.

[6]王世东，郑力，张智海，刘书成.编组站阶段计划自动编制的数学模型及算法 [J].中国铁道科学，2008,29（2）: 120-125.

[7]De Castro LN,Von Zuben F J.Learning and mization Using the Clonal Selection Principle[J].IEEE Transactions on Evolutionary Computation，2002，6（3）：239-251．

Model and Algorithm for Marshalling Station Wagon-flow Optimization

GAN Zhi-xiong,HE Shi-wei,SHEN Yong-sheng,LI Hao-dong,CHENG Jin-xing
（School of Traffic&Transportation,Beijing Jiaotong University,Beijing100044,China）

The paper formulates a mathematical model for the wagon-flow optimization at marshalling stations with given sequences of train making and breaking.It develops an adaptive immune clone algorithm via VC++and uses Lingo11.0 to solve the model.In numerical examples,train properties such as weight,length and axis of cars to be shunted are taken as constraints,which renders the result obtained closer to the fact and more flexible.

marshalling station;scheduling plan;wagon-flow optimization;adaptive immueclone algorithm;Lingo

U292

A

1005-152X（2011）02-0048-04

10.3969/j.issn.1005-152X.2011.02.016

2010-12-13

国家自然科学基金项目（60776825）；北京交通大学优秀博士生创新基金（141076522）；中央高校基本科研业务费专项资金资助（2009YJS042）

甘志雄（1987-），男，江西鄱阳县人，在读硕士研究生，主要研究方向:运输组织现代化。