一个恰含三个圈的本原不可幂定号有向图的基

赵 晶，高玉斌

（中北大学 理学院，山西 太原 030051）

一个恰含三个圈的本原不可幂定号有向图的基

赵 晶，高玉斌

（中北大学 理学院，山西 太原 030051）

为了进一步了解本原不可幂定号有向图的基的特点及有关性质，对一个特殊的本原不可幂定号有向图的基进行了研究．通过分析这个图的特点，运用反证法并结合图中的本原指数、点指数、基指数、Frobenius集、可幂与不可幂及“异圈对”等定义和性质得出基的具体值．

本原；定号有向图；不可幂；基

0 引言

一个实数a的符号sgna，根据a＞ 0，a＜ 0或a= 0，被定义为1，−1或0．将一个有向图D（允许含有环但不能有重弧）中的每一条弧赋予符号1或−1所得的图称为D的定号有向图，记为S，称D为S的基础有向图．定号有向图S中的一条途径W是一个有关弧的序列e1，e2，…，ek，使得ei的终点与ei+1的起点相同，其中i=1， …，k−1，所含弧的条数k被称为途径W的长度，记为l(W).途径W的符号定义为W中所有弧的符号的乘积（重复出现的弧的符号重复计算），即记为sgnW[2]．

1 基本概念与引理

设D是一个有向图，如果存在正整数k，使得对于D中的任意一对顶点vi和vj（可以相同），在D中都存在从vi到vj长为k的途径，则称D为本原有向图．上述最小的k被称为D的本原指数，记为exp(D).设D是一个本原有向图，vi∈D，如果存在正整数p，对任意的t≥p，从顶点vi到D中的任一点都有长为t的途径，那么上述最小的正整数p被称为顶点vi的点指数，记为expD(vi)[3]．设S是一个本原不可幂定号有向图，若对任意顶点vi和vj（可以相同），并且对任意t≥l，从vi到vj都有长为t的SSSD途径，则上述最小的正整数l被称为S的基，记为l(S).W1和W2是S中的两条途径，若它们的起点、终点、长度相同，但符号不同，则称W1和W2为SSSD途径对[4]．若S中不包含SSSD途径对，则称S为可幂的，否则称S为不可幂的[5]．

引理1[6―7]如果S是一个本原定号有向图，那么S不可幂的充分必要条件是S中存在一对长度分别为p1和p2的不同的圈C1和C2，且满足下面两个条件之一：

(a)p1是奇数，p2是偶数，且 sgnC2= −1；

(b)p1和p2都是奇数，且 sgnC1=− sgnC2.

为方便起见，满足条件(a)或(b)的圈对C1和C2称为“异圈对”．容易看出，此时，闭途径对W1=p2C1和W2=p1C2有相同的长度，但有不同的符号：

设R={l1，…，lk}为本原有向图D的圈长的集合，且g.c.d(l1，…，lk)=1．对于D中的每个顶点x和顶点y，设d(x，y)为从 到y的距离，dR(x，y)表示从 到y接触R中每一长度的圈的最小距离．用

引理 2[7]设S是一个n阶本原不可幂定号有向图，其基础图为D．d(S)表示S的直径，W1和W2为从点u到v的长度为r的SSSD途径对，则有

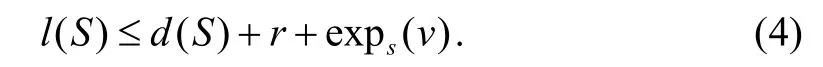
有关定号有向图基的研究，目前取得了一些结果．文献[1]介绍了含有环的本原不可幂定号对称有向图的基；文献[3]介绍了可约符号模式矩阵周期与基；文献[7]给出了几乎可约符号模式矩阵基的界．

本文主要研究一个本原不可幂定号有向图S，其基础图D如图1．容易看出，图1所示的基础图D是由两个圈长为n−5和一个圈长为n−3的3个不同的圈组成的．

图0 定号有向图S的基础图D

2 主要结论

定理1设S是一个n阶（n≥10）本原不可幂定号有向图，基础图D如图1所示，则

定理1证毕．

[1] Gao Yubin，Huang Yihua，Shao Yanling．Bases of primitive non-powerful singed symmetric digraphs with loops[J]．Ars Combinatoria，2009，90：383―388．

[2] Li Z Hall F，Stuart L．Irreducible powerful ray pattern matrices[J]．Linear Algebra Appl，2002，342：47―58．

[3] Liu Bolian．The period and base of a reducible sign pattern matrix[J]．Discrete Mathematics，2007，307：3031―3039．

[4] Gao Yubin，Shao Yanling．Generalized exponents of primitive two-colored digraphs[J]．Linear Algebra and its Applications，2009，430：1550―1565．

[5] Lundgren J R ，Maybee J S．Some properties of a class of recursively defined digraphs[J]．System Sci.，1991，16(1)：29―36．

[6] Wang Longqin，Miao Zhengke，Yan Chao．Local bases of primitive non-powerful signed digraphs[J]．Discrete Mathematics，2009，309：748―754．

[7] Liu Bolian，You Lihua．Bounds on the base of primitive nearly reducible sign pattern matrices[J]．Linear Algebra and its Applications，2006，418：863–881．

Bases of a Primitive Non-powerful Signed Digraph that Just Has Three Cycles

ZHAO Jing, GAO Yu-bin
(North Central University, Taiyuan Shanxi 030051, China)

In order to further understand characteristics and properties of the bases of primitive non-powerful signed digraph, a primitive non-powerful signed digraph with three cycles are studied in this work. By analyzing the features of the digraph, using apagoge and knowledge about primitive exponents, point exponents, bases, Frobenius set, powerful, non-powerful and“distinguished cycle pair”, then the true values of bases are got.

primitive; signed digraph; non-powerful; bases

O157.5

A

1006-5261(2011)05-0001-03

2011-06-14

山西省自然科学基金资助项目（2008011009）

赵晶（1985―），女，山西太原人，硕士研究生；高玉斌（1962―），男，教授，博士，博士生导师．

〔责任编辑 张继金〕