基于SV模型的中国债券信用价差影响因素研究

周荣喜，牛伟宁

（1.北京化工大学 经济管理学院，北京 100029；2.北京航空航天大学 经济管理学院，北京 100191）

基于SV模型的中国债券信用价差影响因素研究

周荣喜1，牛伟宁2

（1.北京化工大学 经济管理学院，北京 100029；2.北京航空航天大学 经济管理学院，北京 100191）

针对中国债券市场，选取2005年6月—2010年6月的企业债和国债月度交易情况，对静态利率期限结构SV参数模型利用遗传算法求解，拟合较为精确的企业债和国债的即期利率曲线，据此计算出企业债的信用价差。在对中国AAA级企业债按不同的期限进行回归分析后发现，该等级债券的信用价差曲线形态呈下降趋势，原因可能是中国债券信用评级过高、担保机制存在问题等；对不同期限企业债信用价差的宏观经济影响因素大致相同，如居民消费价格指数、国内生产总值的变化率等，而且这些信用价差序列之间存在显著的相关关系。

SV模型；遗传算法；信用价差；影响因素；回归分析

一、引 言

信用价差（Credit Spread，简称CS）是指为了补偿信用风险，投资者要求债券提供的高于到期日相同的无风险债券收益的额外收益，它可用于为信用级别不同的各种债券及其信用衍生产品定价或套期保值，帮助投资者和监管部门做出正确的决策。

关于信用价差曲线形态的绝大部分理论和实证研究都得到相似的结论，即高信用级别企业债的信用价差曲线是向上倾斜的，中等信用级别企业债的信用价差期限结构是驼峰状凸起的，低信用级别企业债的信用价差期限结构是向下倾斜的。Helwege等的研究结果表明投机级企业债的信用价差曲线是向上倾斜的［1］；孙克对中国AAA级固定利率上证企业债信用价差进行分析后发现其信用价差曲线是驼峰型的［2］。在信用价差影响因素的相关实证研究方面，Dufresene等总结了信用价差变化的理论因素，建立信用价差的多元线性回归模型后发现，信用价差的改变主要是由那些独立于信用风险因子和流动性指标的特定供求差异引起的［3］；Huang等研究发现罗素2000指数的历史收益率及其波动率、利率的历史波动率、收益曲线的斜率等因子能解释5种债券指数中超过40%信用价差的变动［4］；Wu和Zhang确定了3个基本风险维度—通货膨胀率、实体产出增长率和金融市场波动率，证实了它们与信用价差的关系［5］；Lepone等对澳大利亚债券市场4个不同信用等级和4个不同到期期限范围共8组信用价差数据进行了实证分析，结果表明即期利率和收益率曲线的斜率是信用价差变动的最主要的因素［6］；Tang等研究表明信用价差随国内生产总值、投资者的情绪、公司现金流的增长率和现金流的波动性的变化而变化［7］；任兆璋等认为财务比率方法比结构模型更适合解释我国债券信用价差的变化［8］；张燃的研究表明，短期利率、国债利率差和股票市场回报率对信用价差具有显著影响［9］；谭地军等实证检验了债券特征与债券风险及风险补偿的关系［10］；程文卫的分析表明，通货膨胀变化会对债券的收益率曲线产生明显影响，且与固定收益证券到期收益率和信用利差变化存在显著的协整关系［11］；李杰群等的实证研究表明，债券信用溢价与股指收益率、居民消费价格指数、债券指数收益率、利率期限结构、货币供应增长率之间存在相关关系［12］。从现有的研究情况看，不同期限企业债的信用价差之间的相关关系鲜有经验证据。

目前的实证研究文献在计算信用价差时主要采用线性插值法，有的学者采用相同期限的国债和企业债债券指数收益率之差作为信用价差，如Lepone等［6］；也有文献通过先计算国债收益率，再利用国债收益率模型，将同一时间的企业债券的剩余年限代入等式，求出两个市场中企业债券的无风险收益率数据，最后分别用两个市场的企业债券收益率减去企业债券无风险收益率，得到企业债券与国债的收益率差，如杨晓奇等［13］。这些方法均易导致样本误差过大，使得研究结果很难令人信服。信用价差计算的核心在于确定风险债券和无风险债券的收益率，而对债券即期利率的研究主要采用即期利率期限结构模型，参数模型是其中重要的一类。Nelson等提出NS参数模型［14］，Michalis比较了 NS、SV、三次样条、三种指数样条和VRP方法等7种模型，发现NS、SV和VRP方法要好于其他模型［15］；根据Wu等对信用价差宏观决定因素的无套利分析中采用NS模型拟合企业债即期利率曲线［5］，以及Yu等采用动态NS模型预测国债和企业债收益率的研究结果［16］来看，一定程度上NS模型在拟合企业债的收益率曲线方面有比较优势，但是朱世武等研究认为SV模型更加符合中国实际情况［17］，而在具体求解SV模型过程中，Barrett认为可以事先确定τ1、τ2的值，再利用最小二乘法估计其他参数的值［18］；Manousopoulos等提出可以采用多种非线性最优化方法直接求解SV模型的参数［19］。

本文提出一种新的价差计算方法，即首先选取上交所债券市场企业债和国债多个交易日的数据对SV模型利用遗传算法求解，得到两种债券相对精确的即期利率曲线，据此计算出企业债的信用价差，然后分析中国企业债信用价差的曲线形态，接着研究不同期限企业债信用价差的宏观影响因素以及不同期限企业债信用价差之间的相关关系。

二、SV利率期限结构模型

在SV模型中，假设远期利率为f，则它关于剩余期限t的函数为：

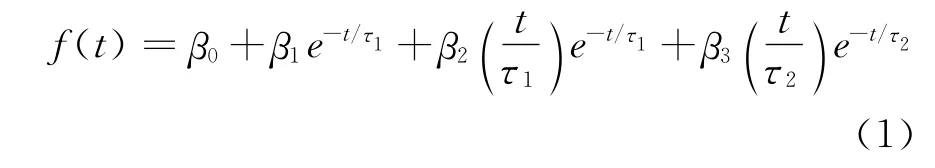
根据即期利率与远期利率关系，在连续复利的情况下，

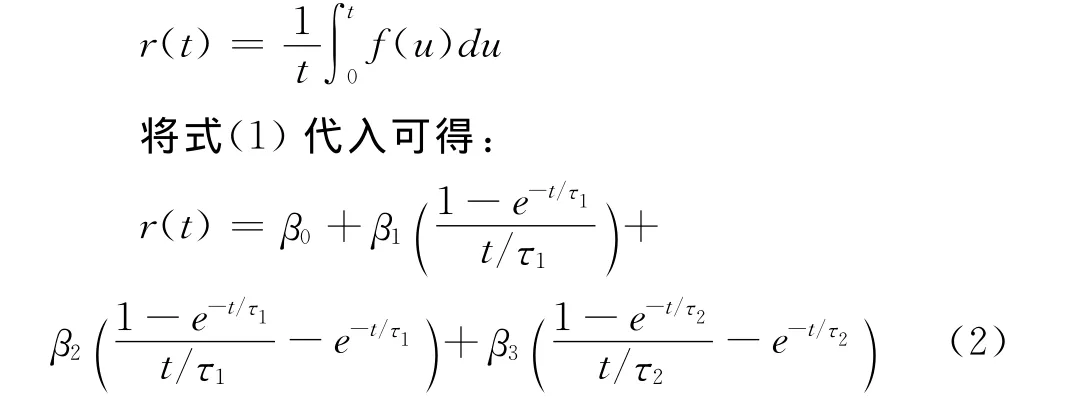
式中，β0表明远期利率曲线的渐近线水平，β0＋β1为远期利率曲线起始点，β2和β3决定了即期利率曲线两个峰的大小和方向，τ1和τ2决定了即期利率曲线峰的具体位置。对式（1）取极限可得：

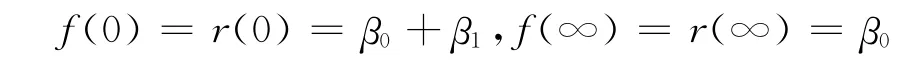
那么折现因子D（t）的就可以表示为：

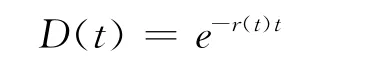
进而可得债券价格的理论值为：

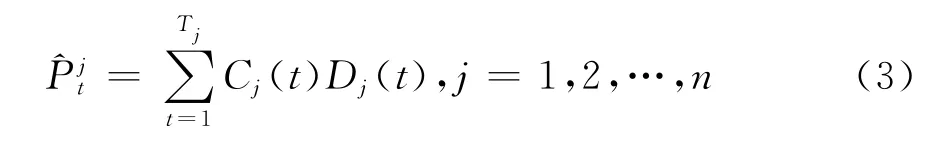
式（3）中T j表示第j支债券的剩余到期期限，Cj（t）表示第j支债券在t时刻的现金流，＾P jt表示第j支债券价格的理论值。在实证分析过程中，若令Pj表示第j支债券的实际价格，当满足所有样本国债的实际价格与理论价格偏差绝对值之和最小这一目标函数时，

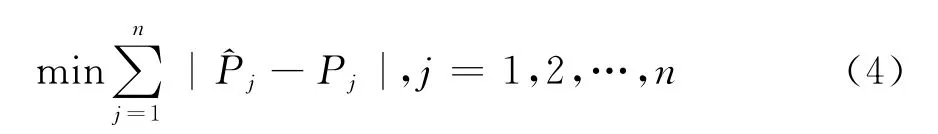
可以得到折现函数D（t）的系数向量的最优估计值，进而可以拟合出国债的即期利率曲线。

三、样本数据及模型求解

（一）样本选取

选取锐思数据库中2005年6月—2010年6月的国债、企业债等变量的统计数据进行实证分析，其中企业债选取信用等级为AAA级、发行期限在2005年6月之前，在样本期内未到期且每个月均有交易数据的企业债，经整理得到每月最后一个、每个企业债均有交易数据的一个交易日的企业债收盘价格、剩余到期期限、票面利率、付息频率、票面价值等；再根据企业债样本的相关交易日整理得到同一交易日的国债收盘价格等样本数据，经筛选有13只企业债和12只国债进行下文的相关实证分析。

相关宏观经济因子选取居民消费价格指数（用CPI表示）、国内生产总值（用GDP表示）、固定资产投资（用INVEST表示）、财政收入（用INCOME表示）、上证综合指数收益率（用INDEX表示）、上海银行间同业拆放利率（用SHIBOR表示）、广义货币供应量（用 M2表示）、狭义货币供应量（用 M1表示）、无风险利率（用RF表示）、企业债指数收益率（用CDINDEX表示）和国债指数收益率（用GBINDEX表示），其中GDP的数据是以季度为单位公布的，因此采用插值法计算样本期内其他月份的数据；数据库中RF是以央行票据的年收益率计算出的月度收益率。本文采用STATA10统计分析软件进行相关回归分析。

（二）参数求解

根据Gimeno等的结论［20］，利用国债的到期收益率估计远期利率，但是根据目前已有的实证研究结论可知，中国国债到期收益率随着剩余期限的增加而增加，且较长期限的到期收益率大于0.3，因此令β0＞0.3；为使利率曲线形状更加符合实际情况，要求β2和β3在（0，1）之间；因τ1和τ2对拟合结果没有太大影响，故可任意选取；因为NS模型与SV模型中β0和β1两个参数的经济含义相同，取值范围也相同，根据唐革榕对NS模型参数取值范围的研究结论［21］，可以给定本文采用SV模型的参数的最终取值范围为β0∈ ［0.3，1］，β1∈ （－1，1），β2∈ （0，1），β3∈ （0，1），τ1∈ （0，10），τ2∈ （20，30）。

利用MATLAB软件，对SV模型采用遗传算法［22］求解参数［β0、β1、β2、β3、τ1、τ2］。

在选取代沟 0.5、交叉概率 0.5、变异概率0.001、染色体数和遗传代数均为1000的情况下得到每个交易日企业债和国债的利率期限结构模型，再选取每个交易日的剩余到期期限分别为1、3、5、7、10、15、20年的国债即期利率和企业债即期利率，二者之差即为信用价差。

四、信用价差曲线形态

（一）各期限企业债信用价差的描述性统计分析

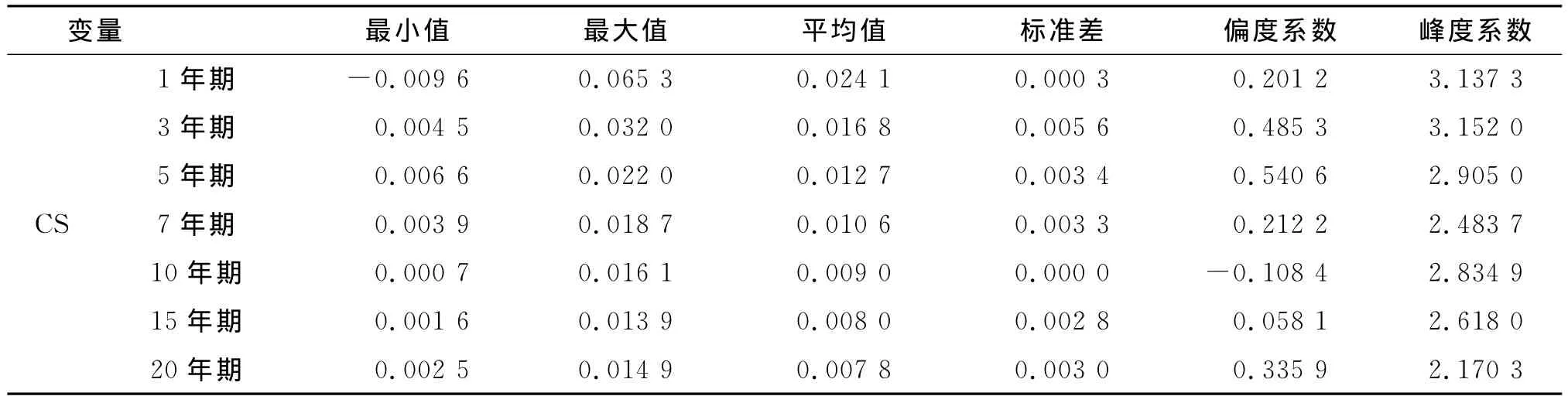
表1 各期限企业债信用价差的描述性统计分析表

从表1中可以看出，具有不同期限企业债的信用价差的平均值显现出不同，并且随着期限的增加呈下降趋势。为了进一步检验不同期限企业债信用价差是否呈显著差异，下文将采用虚拟变量回归方法进行检验。

（二）虚拟变量回归

虚拟变量回归结果如表2所示。其中，reg1表示虚拟变量1，当到期期限为1年时，reg1的值为1，否则为0；相应地，reg2对应于到期期限为3年、reg3对应于到期期限为5年、reg4对应于到期期限为7年、reg5对应于到期期限为10年、reg6对应于到期期限为15年、reg7对应于到期期限为20年的虚拟变量。在虚拟变量回归中，STATA会自动删除其中一个，否则如果包含所有的虚拟变量，将会因为多元共线性导致计算无法进行。从回归结果来看，不同期限企业债信用价差有显著不同；虚拟变量reg5和reg6的系数未通过置信度为95%的t检验，但是从回归系数来看，短期企业债的信用价差要高于中期企业债的信用价差，后者又高于长期企业债的信用价差，说明信用价差随着到期期限的上升而下降。下文将用图形更直观的描绘信用价差曲线形态。

（三）信用价差曲线形态

从图1中可以看到，随着到期期限的增加，信用价差期限结构图呈下降趋势，尽管本文样本企业债的信用等级是AAA级，但它们更像是信用等级较低的企业债。原因可能是评级机构对上市企业债的信用级别评估过高，政府或银行等机构的担保使得信用价差曲线形态表现异常等。

表2 虚拟变量回归分析表

五、信用价差影响因素分析

（一）回归分析

首先对各变量进行描述性统计分析，再对信用价差以及各宏观因子进行相关系数检验，初步验证信用价差与它们的相关关系，进而通过回归分析找到对信用价差有显著影响的宏观因子。建立的回归模型为：

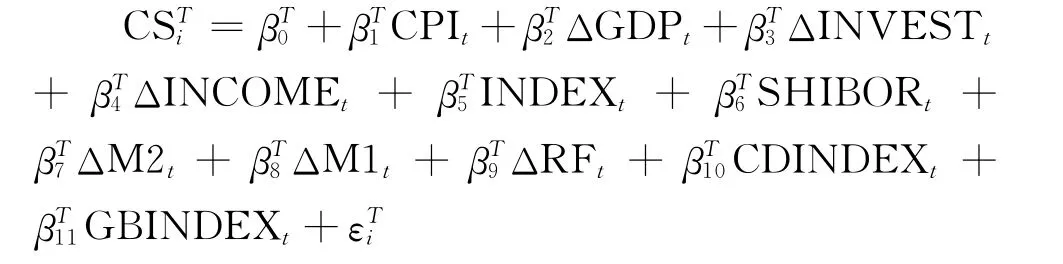
式中，CSTt表示到期期限为T的信用价差；βTi表示第i个变量的回归参数，i＝0，1，2，…，11。回归结果如表3所示。

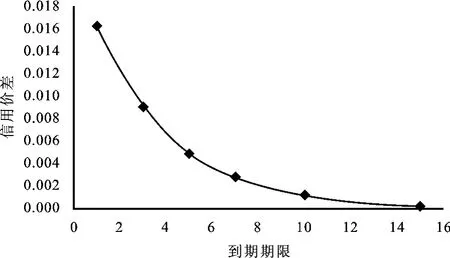
图1 信用价差期限结构图

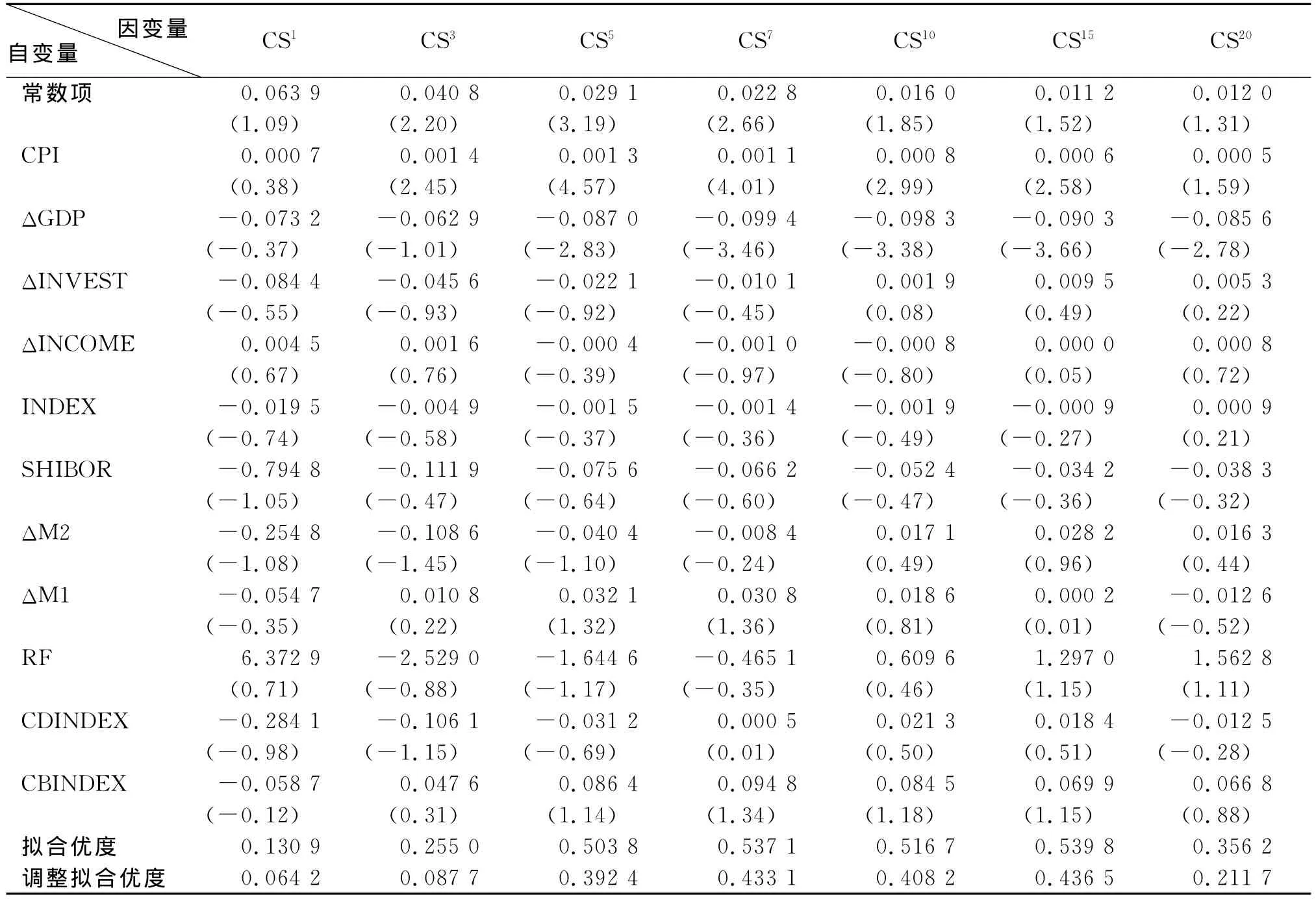
表3 信用价差影响因素回归分析表

（二）模型残差正态性检验

对各期限企业债信用价差回归模型的残差正态性检验结果如表4所示。从表4的检验结果看，除利用20年期的债券信用价差作为因变量进行回归分析时，模型残差正态性检验P值小于0.05外，其他模型的残差P值均大于0.05，可以认为残差呈正态分布，说明模型是有效的。因各自变量之间不存在多重共线性，鉴于模型的残差存在异方差，对其进行稳健回归发现在所有宏观变量中，也只有CPI和ΔGDP的回归系数通过了置信度为95%的t检验。总的来说，回归结果表明，对各期限信用价差有显著影响的宏观经济因子是居民消费价格指数和国内生产总值的变化率。

根据上文模型的回归结果来看，模型的拟合优度均不高，说明仍存在一些对信用价差有显著影响的因子未考虑到模型中。因此，对各回归模型的残差进行主成分分析，以找出对信用价差具有显著影响的变量，结果如表5所示。

从表5的残差主成分分析结果看，前三个主成分的特征值大于1，第一个成分的解释能力达到了45%，前三个主成分的累计解释能力达到了93%，即前三个主成分包含了残差中93%的信息，可以确定主成分的个数为三较合理。第一个主成分中，变量和对其影响最大，因此第一主成分是反映中期企业债信用价差变化的主要宏观影响因子；第二个主成分中，变量ε1和ε3对其影响最大，因此第二主成分是反映短期企业债信用价差变化的主要宏观影响因子；同理，第三个主成分是反映长期企业债信用价差变化的主要宏观影响因子。

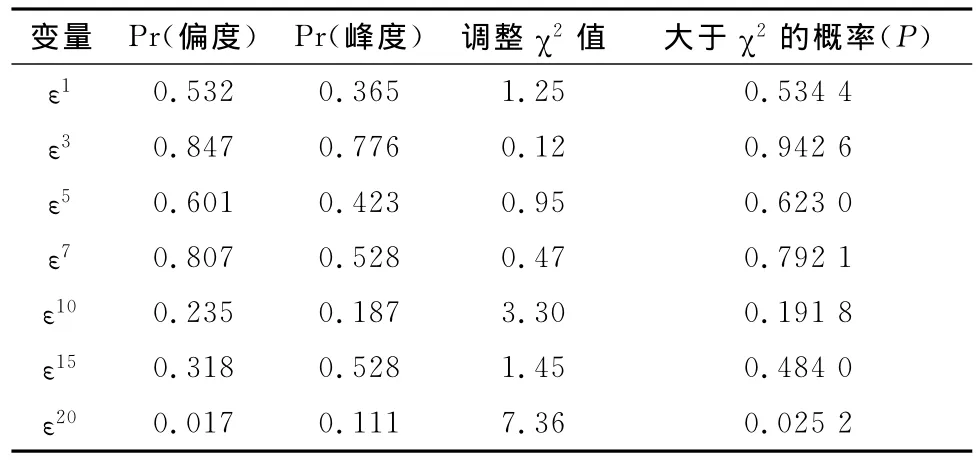
表4 残差正态性检验表

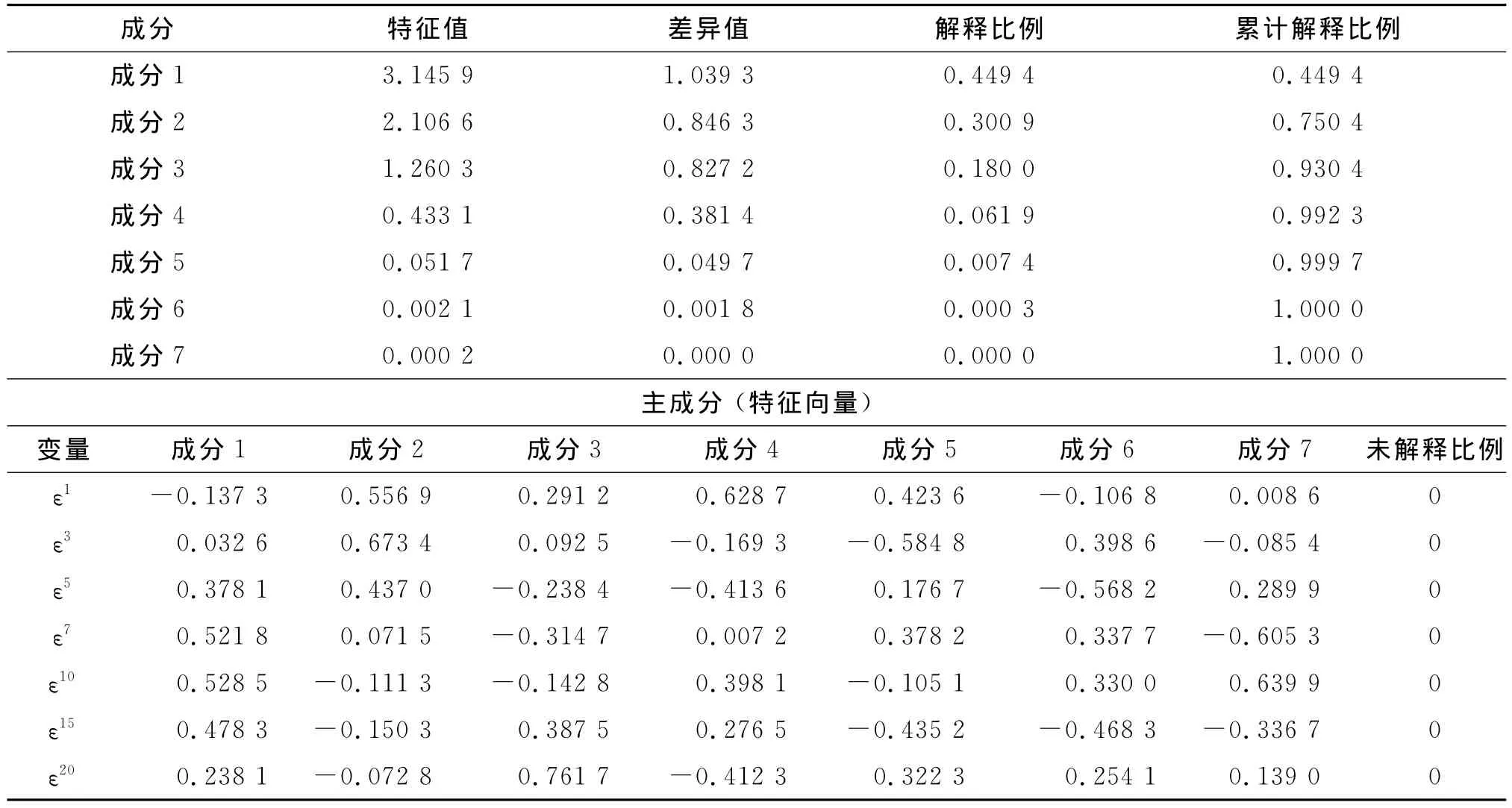
表5 残差主成分分析表

六、模型稳健性检验

到目前为止，本文只根据以往实证文献中证实的影响信用价差变化的宏观经济因子进行了回归分析，如果这些因子能较为综合全面的反映信用价差的变化，模型能解释大部分信用价差变动的原因，鉴于上文的回归结果与此并不相符，说明在我国证券市场中股票和债券市场是存在分割的，也即这些市场是由不同的风险因子驱动的。如果这个结论成立，利用传统的风险估值模型为债券定价是不合适的。另外一种可能就是本文忽略了最重要的某个或一些系统风险解释变量。下面对上文的回归模型进行稳健性检验，加入新的变量再进行回归分析，考虑股票市场波动率（用VI表示）、汇率的波动率（用VE表示）、非线性因素中三年期即期利率的平方（用SQ3表示）和十年期即期利率的平方 （用SQ10表示）。

（一）信用价差之间的相关关系

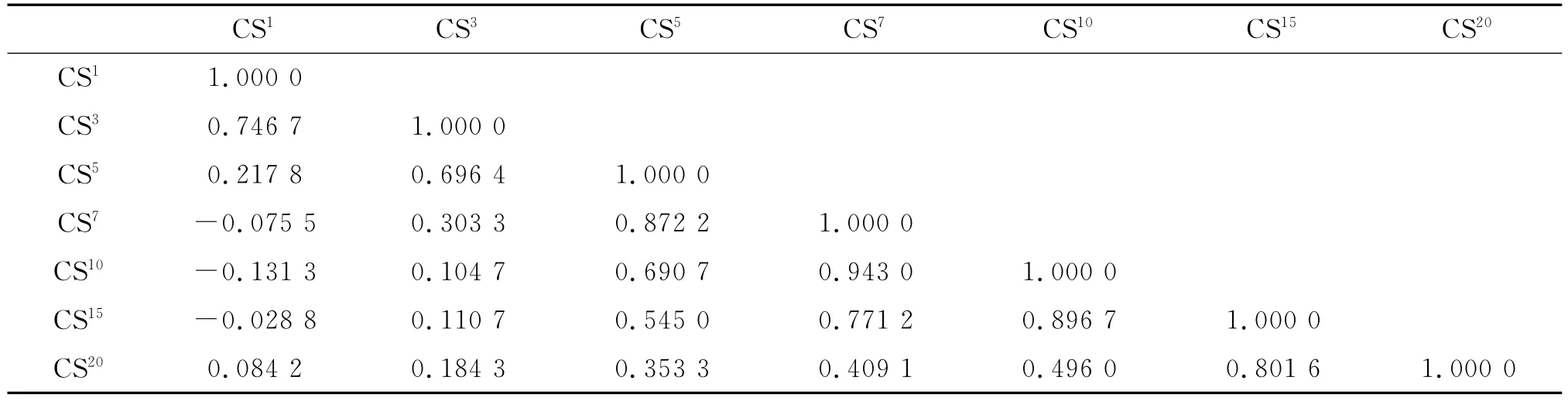
表6 信用价差之间相关系数检验表

从表6信用价差之间的相关系数检验结果可以看出，不同期限企业债的信用价差之间存在强烈的相关关系，因此在对某一期限的信用价差进行分析时可以考虑将其他期限企业债的信用价差作为自变量加入到模型中。

下文首先将四个新加入的变量与第五部分证实的同信用价差有显著相关关系的两个宏观经济因子（CPI和ΔGDP）对信用价差的共同影响进行分析，然后再将这些变量中的显著影响因子同其他期限的信用价差一起分析。

（二）回归分析

1.对新变量的回归分析

从表7的回归结果看，加入新的变量后，除了CPI和ΔGDP因子，对短期信用价差有显著影响的变量是两个非线性因子，即三年期即期利率的平方和十年期即期利率的平方；各变量几乎都对中期信用价差有显著影响，它们的相关系数基本上都通过了置信度为95%的t检验；不同的是，非线性因子对长期信用价差的影响不大，股票市场波动率和汇率波动率对15年期信用价差的影响要显著于20年期信用价差。与上文的回归模型相比，加入新变量后模型的拟合优度均有大幅度提高，说明新加入的变量对信用价差还是有显著影响的。下面将对各回归模型的残差进行正态性检验，以检验模型是否有效。用!T表示分别对各期限信用价差回归分析时的残差，对其进行正态性检验结果如表8所示。由于所有模型的残差均呈正态分布，表8的检验结果表明上述模型是有效的。

表7 信用价差影响因素回归分析表

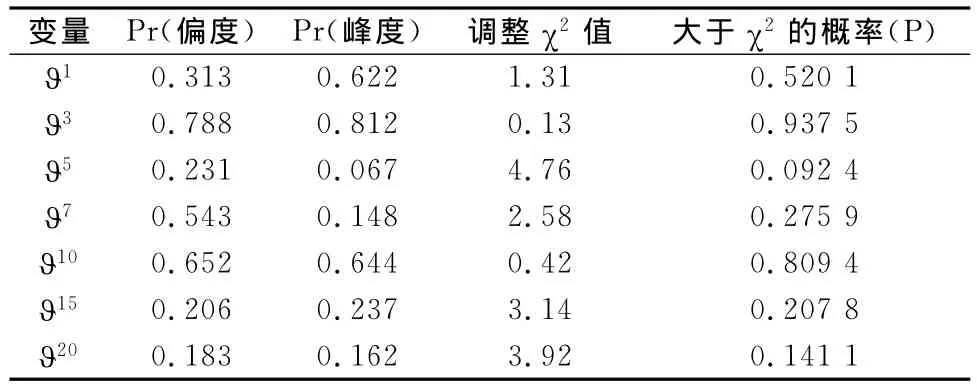
表8 残差正态性检验表

2.信用价差之间的相关关系

根据上文的分析，各因子对信用价差都有影响，下文将这些影响因子同其他期限的信用价差一起分析。回归结果如表9所示。

从表9的回归结果看，考虑其他期限的信用价差后，除了1年期信用价差，其他模型的解释能力几乎达到了100%；但是，宏观经济因子对模型几乎没有解释能力，即便在对7年期和10年期的信用价差进行回归分析时，CPI这一变量的系数通过了置信度为95%的t检验值，鉴于回归系数仅为0.000 1，数值太小，其影响可以忽略，因此可以说，不同期限的信用价差之间均有显著的相关关系；在对其中一个期限企业债的信用价差进行分析时，可以看到，对该期限信用价差有显著影响的其他期限的信用价差随着距离的上升而下降，举例来说，如5年期信用价差，对其影响较大的是3年期和7年期信用价差，而1年期和10年期、15年期信用价差则随着同5年期信用价差的距离上升而下降，对其他期限的信用价差进行分析时也得到同样的效果。用ηT表示分别对各期限信用价差回归分析时的残差，对其进行正态性检验结果如表10所示。

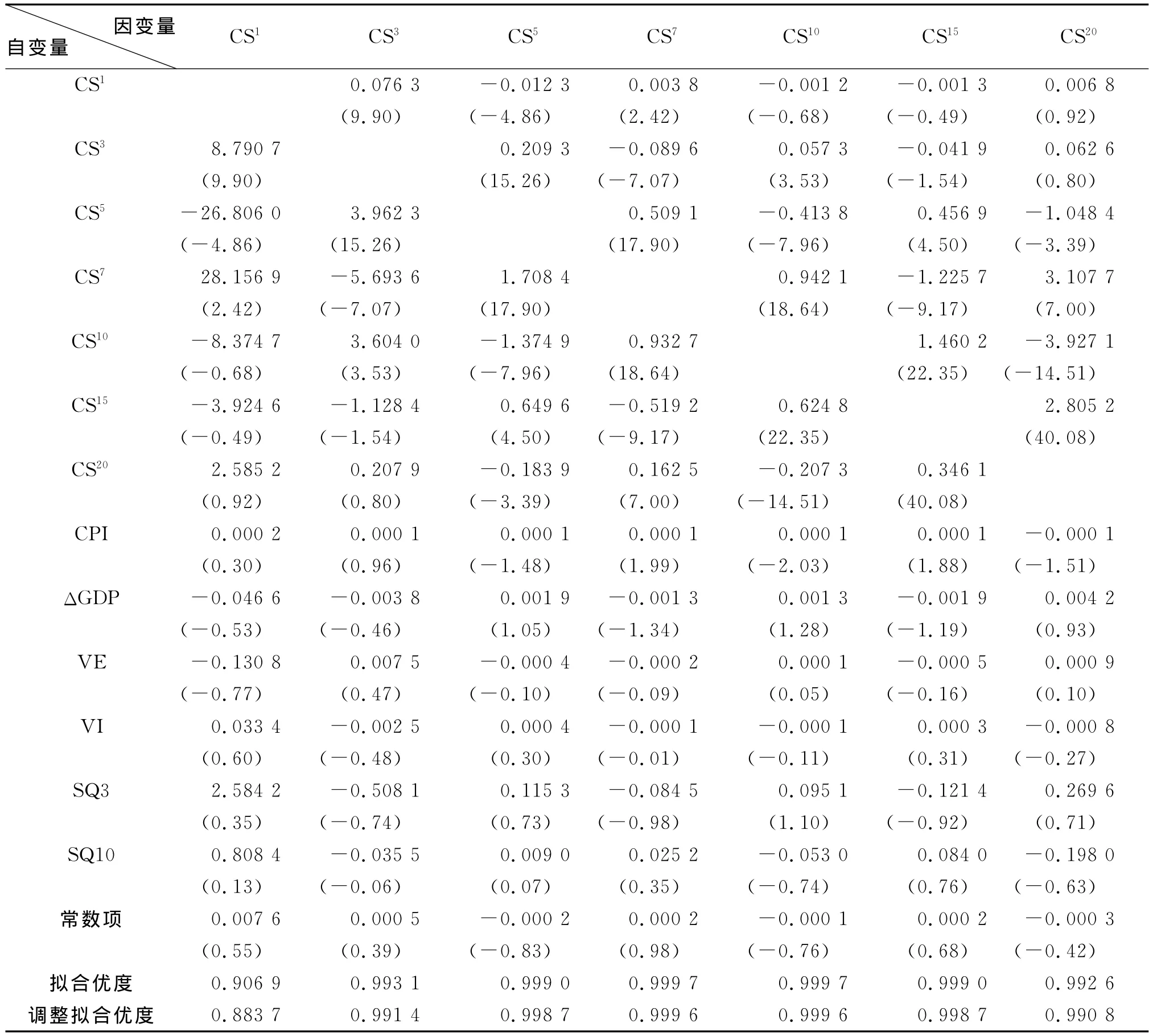
表9 不同期限信用价差之间的相关关系回归分析表

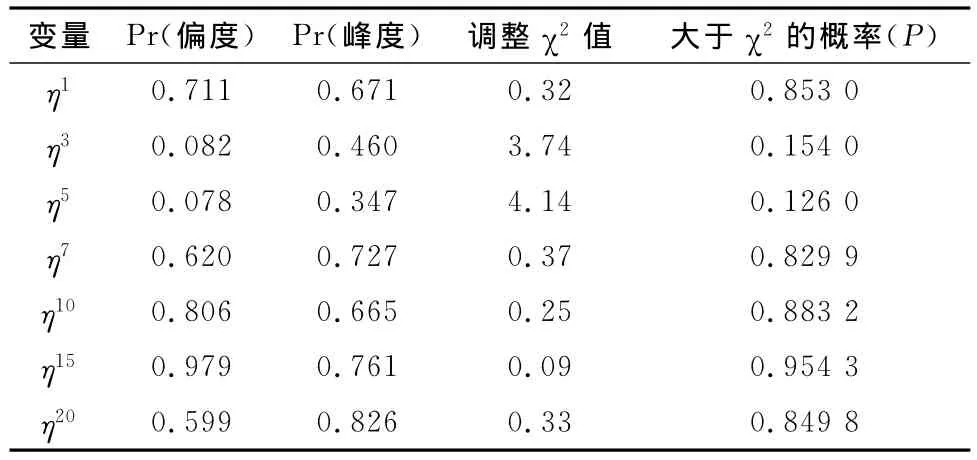
表10 残差正态性检验表

从表10的检验结果看，因所有残差的P检验值均远大于0.05，说明模型是有效的。信用价差序列之间的强相关关系表明，如果想通过企业债投资组合来消除违约风险，即使投资规模非常庞大，实现组合的违约风险完全分散掉是不太可能的。

七、实证分析结论

本文选取2005年6月—2010年6月的企业债与国债相关交易情况和宏观经济因子的月度数据，采用SV模型求出债券信用价差后，将其分为不同的期限，首先采用虚拟变量回归的结果发现，信用价差曲线形态呈下降趋势，这与大多数学者的研究结论不相符。鉴于本文采用的是AAA级企业债，造成这种情况的原因可能是中国债券信用评级过高、担保机制存在问题等导致的。

分期限对短、中、长期债券信用价差进行回归分析后发现，采用SV模型计算出的信用价差的显著影响因素只有CPI和ΔGDP，且模型的解释能力较低，最高的也只有50%左右。对这些回归模型的残差进行主成分分析后，结果表明，第一个成分的解释能力达到了45%，前两个主成分的累计解释能力达到了75%。因此，根据目前相关文献采用的其他宏观因子，除了CPI和ΔGDP，本文接下来还考虑了股票市场波动率、汇率波动率、非线性因子等对不同期限的信用价差的影响，回归结果显示，模型的解释能力有所提高，且新加入的各变量均对信用价差有显著影响。

在对不同期限的信用价差进行相关分析时发现，它们之间存在显著的相关关系，因此，本文最后不仅考虑了宏观经济因子对信用价差的影响，而且在对其中一个期限的信用价差进行分析时还加入了其他期限信用价差对它的影响。结果表明，对某一期限信用价差有显著影响的其他期限的信用价差随着与它距离的上升而下降，也就是说，期限越近的信用价差之间存在越强的相关关系，随着期限的延长，影响越弱。

本文不足之处在于论文主要采用回归模型进行分析，研究结果可能会有一定的误差，可以考虑扩大样本区间，采用时间序列法进行分析，得到更有说服力的结论。另外，本文主要研究不同交易市场国债之间的利差以及国债与企业债之间的信用价差，还可将研究对象推广至其他类型的有违约风险的债券（如短期融资券、商业银行债、中期票据等）与国债之间的价差，以及同种债券不同信用等级之间的价差等。

［1］ Helwege J，Turner C M.The Slope of the Credit Yield Curve for Speculative Grade Issuers［J］.Journal of Finance，1999，54（5）.

［2］ 孙克.企业债信用价差曲线形态验证与政策启示［J］.证券市场导报，2009（4）.

［3］ Dufresene C，Goldstein P，Martin R.The Determinates of Credits Spread Changes［J］.Journal of Finance，2001（6）.

［4］ Huang J，Kong W.Explaining Credit Spread Changes：New Evidence from Option－Adjusted Bond Indexes［J］.The Journal of Derivatives，2003，11（1）.

［5］ Wu L，Zhang F X.A No－Arbitrage Analysis of Macroeconomic Determinants of the Credit Spread Term Structure［J］.Management Science，2008，54（6）.

［6］ Lepone A，Wong B.Determinants of Credit Spread Changes：Evidence from the Australian Bond Market［J］.The Australasian Accounting Business ＆ Finance Journal，2009，3（2）.

［7］ Tang D Y，Yan H.Market Conditions，Default Risk and Credit Spreads ［J］.Journal of Banking ＆ Finance，2010，34（4）.

［8］ 任兆璋，李鹏.中国企业债券价差个体性影响因素的实证分析［J］.华南理工大学学报：社会科学版，2006，8（1）.

［9］ 张燃.信用价差变化的决定因素——一个宏观视角［J］.当代财经，2008（9）.

［10］谭地军，田益祥，黄文光.中国企业债券特征与风险补偿［J］.数量经济技术经济研究，2008，25（2）.

［11］程文卫.通货膨胀对固定收益证券到期收益率和信用利差的影响：基于中国的实证研究［J］.中央财经大学学报，2009（7）.

［12］李杰群，齐新宇，赵庆，胡延坡.我国公司债券信用溢价的实证研究［J］.上海财经大学学报，2010，12（5）.

［13］杨晓奇，陈冠华.关于我国企业债券市场利差的实证研究［J］.财会月刊，2010（11）.

［14］Nelson C R，Siegel A F.Parsimonious Modeling of Yield Curves［J］.Journal of Business，1987，60（4）.

［15］Michalis I.A Comparison of Yield Curve Estimation Techniques Using UK Data［J］.Journal of Banking ＆ Finance，2003，27（1）.

［16］Yu W C，Zivot E.Forecasting the Term Structures of Treasury and Corporate Yields Using Dynamic Nelson－Siegel Models［J］.International Journal of Forecasting，2011，27（2）.

［17］朱世武，陈健恒.交易所国债利率期限结构实证研究［J］.金融研究，2003，24（10）.

［18］Barrett W B.Term Structure Modeling for Pension Liability Discounting［J］.Financial Analysts Journal，1988，44（6）.

［19］Manousopoulos P，Michalopoulos M.Comparison of Non－linear Optimization Algorithms for Yield Curve Estimation［J］.European Journal of Operational Research，2009，192（2）.

［20］Gimeno R，Nave J M.A Genetic Algorithm Estimation of the Term Structure of Interest Rates［J］.Computational Statics and Data Analysis，2009，53（6）.

［21］唐革榕.我国利率期限结构的静态拟合实证研究［D］.厦门：厦门大学博士学位论文，2006.

［22］白小莹，周荣喜，杨丰梅.基于遗传算法的多项式样条函数利率期限结构模型［J］.系统工种，2009，27（7）.

Research on the Factors Affecting Credit Spreads of China＇s Bonds Based on SV Model

ZHOU Rong-xi1，NIU Wei-ning1，2

（1.School of Economics and Management，Beijing University of Chemical Technology，Beijing 100029，China；2.School of Economics and Management，Beihang University，Beijing 100191，China）

As to China＇s bonds market，the paper selects some trading information of corporate bonds and treasury bonds on a monthly basis，after solving Svensson（1995）model of term structure of interest rates through genetic algorithm，the more exact yield curves of both types of bonds can be obtained，based on which the credit spreads between them generate.After regression analysis of China＇s bonds of different terms of maturity but with the same credit rating AAA，it can be concluded that the curve of credit spreads show a downward trend，the reasons for which owe to over－high credit rating of our country＇s bonds and a non－perfect security mechanism.What＇s more，the factors which have different effects on the variation of credit spreads in different maturity are almost the same，such as CPI and GDP，and there is a significant positive correlation among credit spreads series.

SV model；genetic algorithm；credit spreads；macroeconomic factors；regression analysis

（责任编辑：王南丰）

C934

A

1007－3116（2011）12－0080－09

2011－06－07

国家自然科学基金《基于非参数仿射期限结构模型的利率衍生产品定价集成研究》（70701003）；国家自然科学基金《基于期限结构模型的中国债券信用利差体系研究》（71171012）；中央高校基本科研业务费专项资金《基于利率期限结构组合优化模型的我国债券信用价差体系研究》（ZZ1017）；北京化工大学发展中学科建设项目《三类金融产品定价及其风险管理策略研究》（2010096）

周荣喜，男，江西崇仁人，管理学博士，教授，研究方向：金融工程、决策分析；

牛伟宁，女，河南南阳人，博士生，研究方向：金融工程。

【统计应用研究】