MCMC方法下最优Copula的估计及选取

蔡晓薇

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233000）

MCMC方法下最优Copula的估计及选取

蔡晓薇

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233000）

针对目前Copula函数在实际中的应用问题，介绍了一种基于马尔科夫链蒙特卡罗方法（MCMC）的Copula函数估计及选取方法，并将该方法与目前常用方法进行系统比较，最后对上证综合指数和深证成分指数进行了实证分析，结果体现了该法的有效性。

Copula函数；MCMC方法；DIC信息准则

一、引 言

Copula函数可以将多个随机变量的边缘分布连接在一起形成联合分布，变量间的相关结构完全由Copula函数决定，而各变量间的统计特征由其边缘分布决定。此外，若对随机变量做单调增变换，由Copula函数导出的一致性和相关性测度的值不会改变，可以捕获随机变量间非线性的相关关系。因此，Copula函数模型被广泛应用于风险管理、资产定价、多变量金融时间序列分析等方面［1］129－152，［2］132－158。

运用Copula函数建模主要有两个步骤：（1）确定随机变量的边缘分布；（2）最优Copula函数的确定。而最佳边缘分布及最优Copula函数尤其是后者的确定一直以来是建模中的难点，虽然许多学者提出了一些相应的建议，但是这一问题还是没得到很好地解决。本文运用 MCMC（Markov Chain Monte Carlo）方法对Copula函数模型进行估计，并提出了一种基于DIC（Deviance information criterion）信息准则的选择方法，该方法无需对原样本数据进行任何变换，是一个强力有效的最优Copula函数及其模型的选取方法。

二、Copula函数

Nelsen对N维Copula函数定义为具有以下性质的函数C：（1）C＝I N＝ ［0，1］N；（2）C的边缘分布Cn（·）满足Cn（un）＝C（1，…，1，un，1…1）＝un，其中，u∈［0，1］，n∈［1，N］；（3）C对它的每一个变量都是递增的［3］227－250。

显然，一个N维Copula函数是一个N维概率分布函数，其边缘分布是限制在［0，1］N上的均匀分布，在二维情况下，如果F1（x1），F2（x2）是随机变量X1，X2的分布函数，那么C（F1（x1），F2（x2））可以作为（X1，X2）的联合分布函数。

目前常用的Copula函数估计方法主要有以下几种：精确极大似然估计法（EML），该方法需要已知边缘分布，其缺陷是当碰到高维数据时，会有很大的计算量；分步极大似然估计法（IFM），该方法也需已知边缘分布，对参数的θ的估计分为2步，缓解了计算量的问题，但估计2次会导致误差积累放大；规范化的极大似然估计法（CML），从理论上来讲，CML是以上三种估计方法中最好的方法，因为它没有对边缘分布形式作出假设。如果对边缘分布的形式作出错误的判断，EML和IFM方法将改变变量间的相依结构；非参数估计方法，该方法较其他方法来说计算简单，但使用范围主要适用于Archimedean Copulas。

对于最优Copula函数的选取，基于Copula分布函数与条件分布的QQ图法直观、快捷，但其缺乏量化的标准，且有时无法辨别图形间微小差别；计算并比较理论Copula函数＾C与经验Copula函数Cn之间的距离，也是比较常用的方法；Roberto De Matteis和Dobric et al.分别提出了基于K－S检验与P维χ2检验的拟合优度检验［4］，Daniel Berg对Copula函数选取的拟合优度检验做了系统的总结和比较［5］；Chen和Fan提出一种伪似然比检验方法来选择最优Copula函数；Huard et al.建议一种基于贝叶斯理论的Copula函数选取方法。以上方法基本均需对原变量序列进行数据变换，因此会对样本数据信息造成一定的丢损。

三、Copula函数模型的贝叶斯分析

（一）模型的贝叶斯推断

根据贝叶斯定理，对Copula函数模型进行贝叶斯推断，关键是在已知观察数据下，获得模型参数的后验分布。即π（Ψ）∝l（Ψ）p（Ψ），其中Ψ为Copula函数的参数与边缘分布函数的参数组成的参数向量，π（Ψ）、l（Ψ）、p（Ψ）分别为相应的后验分布、似然函数、先验分布。

为不失一般性，令（X1，X2）为一二维连续随机变量，那么其在Copula函数下相应的联合概率密度函数为：

其中，F1、F2与f1、f2分别为相应变量的边缘分布函数与边缘密度函数，c为Copula函数的概率密度函数。

如果X＝ （（x11，x21），…，（x1n，x2n））是上述分布的一个i.i.d样本，那么其似然函数为［6］31－83：

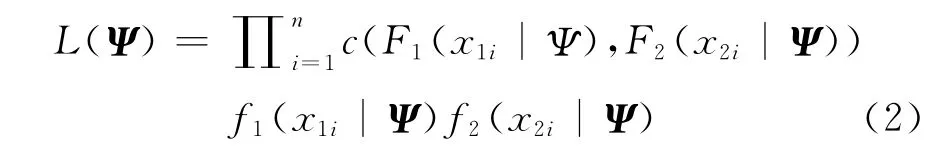
这样，在已知Copula函数模型参数向量的先验分布时，就可以得到其后验分布的核。

（二）MCMC方法

MCMC方法是使用马尔科夫链的蒙特卡罗积分，其基本思想是：构造一条Markov链，使其平稳分布为待估参数的后验分布，通过这条马尔科夫链产生的后验分布的样本，并给予马尔科夫链达到平稳分布时的样本进行蒙特卡罗积分。在采用MCMC方法时，马尔科夫链转移核的构造至关重要，不同的转移核构造方法，将产生不同的MCMC方法，目前常用的MCMC方法主要有两种，Gibbs抽样和Metropolis－Hastings算法。

Metropolis－Hastings算法是比较一般化的MCMC方法［7］176－235，该方法的基本思路是：任意选择一个不可约转移概率q（·，·）以及一个函数α（·，·），0＜α（·，·）≤1，对任一组合（x，x′）（x≠x′），定义：

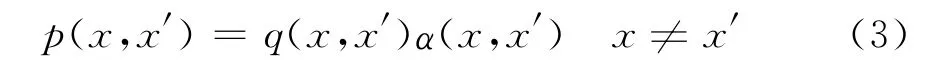
则p（x，x′）形成一个转移核。在有了q（·，·）后，应选择一个α（·，·），使相应的p（x，x′）以π（x）为其平稳分布，最常用的选择是：

此法的实施比较直观：如果链在t时刻处于状态x，即X t＝x，则首先由q（·，x）产生一个潜在的转移x→x′，然后根据概率α（x，x′）决定是否转移。即以概率α（x，x′）接受x′作为下一时刻的状态值，以1－α（x，x′）拒绝转移到x′，而链的下一时刻仍处于状态x。于是，在有了x′后，可再抽取一个［0，1］上均匀分布的随机数u，则：

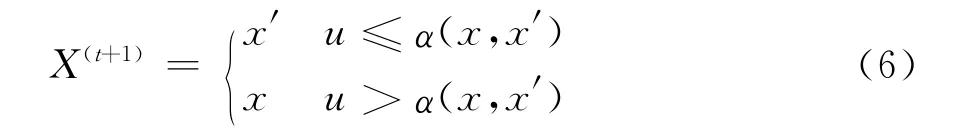
一 般 称q（·，·） 为 建 议 分 布 （proposal distribution），目的是使后验分布π（x）成为平稳分布， 建 议 分 布q（x，x′） 可 以 取 各 种 形 式。Metropolis（1953）采用了对称的建议分布，即：

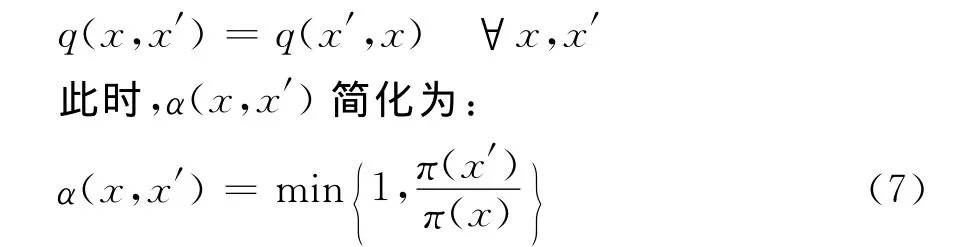
对称建议分布的一个特列是q（x，x′）＝q（｜xx′｜），这称为随机漫步Metropolis算法。

（三）DIC准则

DIC准则（Deviance Information Criterion）是由Spiegelhlter et al.提出的。DIC准则同时考虑了模型对数据的拟合优度以及模型的复杂程度，其值可以很容易从Markov chain Monte Carlo结果计算出，并且不需要对原样本数据进行任何变换。

如果L（X｜Ψk，M k）表示Copula函数模型M k的似然函数，则定义偏差函数为［8］：

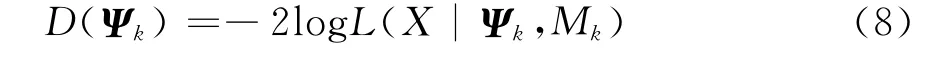
定义DIC准则下模型M k参数的有效个数为：

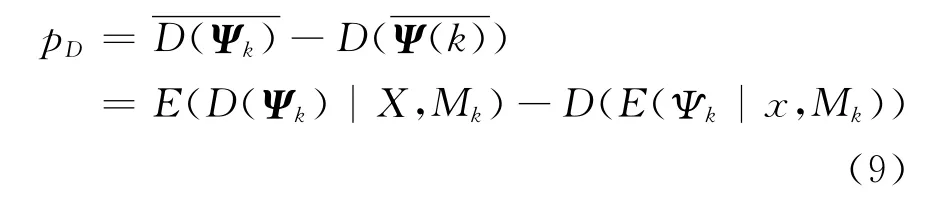
则Copula函数模型的DIC准则为：

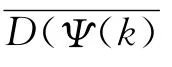
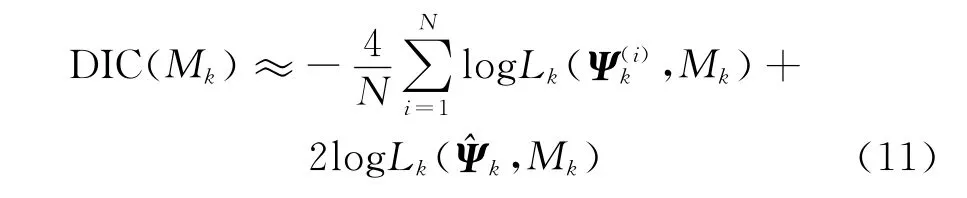
为作比较，本文同样也计算了Copula函数模型的AIC、BIC以及二者的扩展EAIC、EBIC准则：其中，d k为Copula函数模型M k中的参数个数。

四、实证模拟研究

（一）模型的设置

为比较MCMC估计效果及DIC检验功效，基于二维Copula函数，选取了 Normal Copula、T Copula、Gumbel Copula、Frank Copula、Clayton Copula、Galambos Copula，2支椭球 Copula，3支阿基米德Copula函数，1支极值Copula函数，共6支具不同相依结构的Copula函数。其中，Normal Copula、T Copula、Frank Copula密度函数具有对称性，且尾部是渐进独立的，Gumbel Copula、Galambos Copula密度函数具有非对称性，具有上尾相关性，Clayton Copula密度函数也是非对称性的，具有下尾相关性。此外，对于T Copula函数，将其自由度固定为4。

表1 本文选用Copula函数的概率密度函数

对于边际分布函数，选取了4个不同的边际分布来刻画研究对象。第一个是经典的正态分布（Normal distribution），如果变量X服从均值为μ和方差为σ2的正态分布，那么其概率密度函数和分布函数分别为：

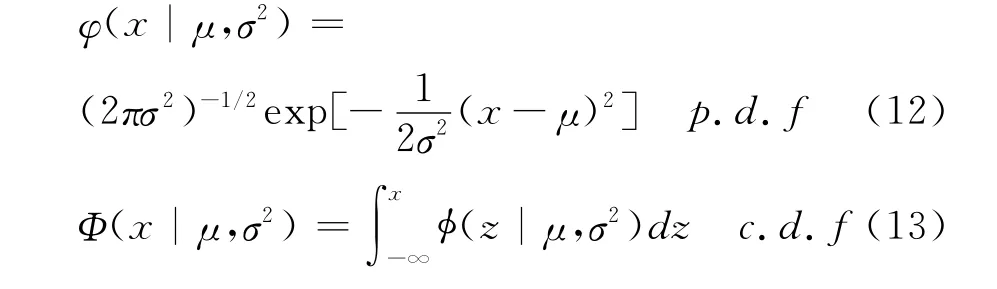
第二个边际分布为逻辑斯蒂分布（Logistic distribution），Logistic分布类似于正态分布，但尾部比正态分布要厚，如果变量X服从位置参数μ和尺度参数σ的Logistic分布，那么其概率密度函数和分布函数分别为：

第三个边际分布为拉普拉斯分布（Laplace distribution），Laplace分布同样也是一厚尾分布，如果变量X服从位置参数μ和尺度参数σ的Laplace分布，那么其概率密度函数和分布函数为：

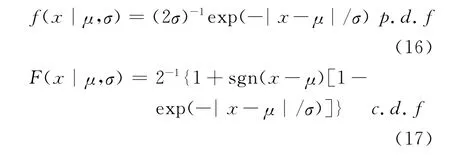
最后一个分布我们选择的是非对称拉普拉斯分布（Asymmetric Laplace distribution），ALaplace分布是上述Laplace分布的推广，如果变量X服从位置参数μ、尺度参数σ和形状参数λ的ALaplace分布，那么其概率密度函数和分布函数为：

对于先验分布，本文对模型的参数赋予独立的且方差足够大的已知分布，进而避免对Copula函数模型引入过多的先验信息，使得模型的选择准则主要是基于数据信息［9－10］。对Copula函数的先验分布，主要基于其参数的定义区间来确定相应的先验分布，如对Normal Copula与T Copula选用均匀分布，对Clayton Copula选用伽玛分布；对边缘分布，其位置参数选用正态分布作其先验分布，尺度参数的先验选用逆伽玛分布。

（二）模拟研究

样本数据选用上海证券综合指数（SHCI）和深圳证券成分指数（SZCI）的日收盘价为实证研究对象建立Copula函数模型。样本区间为1996年12月16日至2009年5月5日，样本容量299 1。将价格市场指数每日收盘价定义为Pt，则对数收益率定义Rt＝ln（Pt）－ln（P t－1），数据来源于大智慧软件。

由SHCI与SZCI收益率序列基本统计特征的偏度、峰度及Jarque－Bera检验值可以看出，二序列呈现明显的尖峰厚尾特征，须用尖峰厚尾分布对其拟合，如Laplace分布、Logistic分布、极值分布、稳定分布、混合分布等。

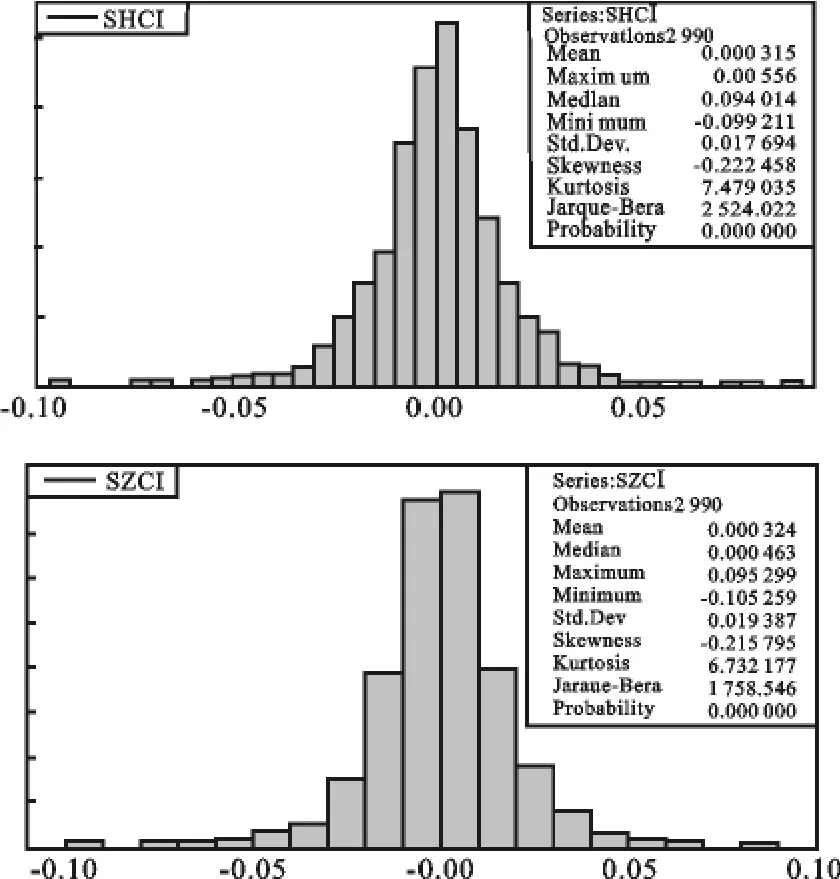
图1 SHCI与SZCI的基本统计特征图

基于MCMC模拟的Bayes推断都是在假设Markov链已经达到稳定状态下进行的，因而判断Markov链的收敛性对Bayes估计推断是非常重要的。运用Matlab和R软件对6支Copula函数在各边缘分布下分4组进行MCMC模拟，每次模拟都先进行了5 000次预迭代，然后舍弃原来的迭代再进行20 000次迭代，以保证Markov链的收敛性，最后每次模拟的结果均进行并通过了Geweke谱密度收敛性诊断、Heidelberger－Welch收敛性诊断、Gelman－Rubin方差比收敛性诊断以及Raferty－Lewis收敛性诊断。

由表2各组Copula函数模型的DIC、AIC、EAIC、BIC、EBIC以及PD值可以得到以下几个结论：（1）对于相同Copula函数下，具有不同边缘分布的Copula函数模型，Alaplace分布能够更好地拟合SHCI与SZCI的收益率序列，并且拟合效果为：Alaplace＞Laplace＞Logistic＞Normal；（2）相同边缘分布下，由不同Copula函数连接的Copula函数模型，Student Copula相比其他Copula函数可以更好地刻画SHCI与SZCI的相依结构；（3）上述两种情况下，DIC准则的模型选择结果与AIC、EAIC、BIC、EBIC准则的检验结果一致。在本文所有研究模型中，T Copula－Alaplace模型为拟合SHCI与SZCI的最佳模型。

五、结论与展望

1.不同的Copula函数连接不同边缘分布建立的Copula函数模型的相依结构不同，拟合效果也不同。因此，在实际运用Copula函数建模时，边缘分布与Copula函数的选择都非常重要，尤其是Copula函数的选择。

2.在本文选用的Copula函数模型中，T Copula－Alaplace模型为拟合SHCI与SZCI序列的最佳模型，但我们还可以用其他的边缘分布如GARCH模型族、稳定分布、混合分布等以及其他Copula函数如混合Copula函数等来获得更佳的拟合模型。

表2 Copula函数模型的DIC、AIC、EAIC、BIC、EBIC值

3.基于Bayes理论的MCMC方法可以在不对 原数据进行任何变换的情况下估计Copula函数模型，而基于MCMC后验抽样分布的DIC准则同其他信息准则如AIC准则、BIC准则同样有效。DIC准则是Copula函数模型以及其他模型选择的一个强力有效工具，但要注意的是该法要求Copula函数的密度函数是确定的。

［1］ Cherubini U.Copula Methods in Finance［M］.Hoboken：John Wiley，2004.

［2］ 韦艳华，张世英.Copula理论及其在金融分析上的应用［M］.北京：清华大学出版社，2008.

［3］ Nelsen B.An introduction to Copulas，Second Edition［M］.New York：Springer，2006.

［4］ Daniel Berg.Copula Goodness－of－fit Testing：Overview and Power Comparison［J］.Taylor and Francis Journals，2009，15（7－8）.

［5］ Fermanian J D.Goodness－of－Fit Tests for Copulas［J］.J Multivariate Anal，2005，95（11）.

［6］ Ioannis Ntzoufras.Bayesian Modeling Using Winbugs［M］.Canada：John Wiley ＆Sons，2009.

［7］ Dani Gamerman，Hedibert Freitas Lopes.Markov Chain Mente Carlo：Stochastic Simulation for Bayesian Inference［M］.Boca Raton：Taylor ＆Francis，2006.

［8］ Celeux G，Forbes F，Robert C P，Titterington D M.Deviance Information Criteria for Missing Data Models［J］.Bayes.Anal.，2005，1（4）.

［9］ David Huard，Guillaume Evin，Anne－Catherine Favre.Bayesian Copula Selection［J］.Computational Statistics ＆ Data Analysis，2006，51（2）.

［10］Ralph dos Santos Silva，Hedibert Freitas Lopes.Copula，Marginal Distributions and Model Selection：A Bayesian Note［J］.Statistics and Computing，2008，118（3）.

The Estimation and Selection of Optimal Copula Model Based on MCMC Method

CAI Xiao-wei

（School of Statistics and Applied Mathematics，Anhui University of Finance and Economics，Bengbu 233030，China）

In order to identify the optimal Copula，a new Copula estimation and selection method based on Markov chain Monte Carlo is proposed，and the method is compared with the other methods in popularity.At last，we apply the proposed method to Shanghai Stock Composite Index and Shenzhen Stock Component Index，and the results reflect the effectiveness of the method.

Copula；Markov Chain Monte Carlo；deviance information criteria

（责任编辑：王南丰）

O212.8

A

1007－3116（2011）10－0033－06

【统计应用研究】