中国农产品期货市场的多重分形特征及其成因分析——基于MF－DFA分析法

李志慧，卢新生

（西北农林科技大学 经济管理学院，陕西 杨凌 712100）

中国农产品期货市场的多重分形特征及其成因分析
——基于MF－DFA分析法

李志慧，卢新生

（西北农林科技大学 经济管理学院，陕西 杨凌 712100）

运用多重分形消除趋势波动分析方法（MF－DFA）和多重分形谱分析法，对中国豆一、玉米、硬麦、强麦4种主要农产品期货价格波动的多重分形特征进行了实证分析和比较。研究发现：中国农产品期货市场存在显著的多重分形特征，硬麦、强麦、玉米和豆一期货的多重分形性依次减弱。通过对原始数据的重排和相位随机化处理，可以看出中国农产品期货市场的多重分形特征是由长程相关性和收益序列的厚尾概率分布两个因素共同导致，其中非正态分布起主导作用。

农产品期货；多重分形；趋势波动分析方法；多重分形谱；长程相关性

一、引 言

大多数有关金融资产价格波动的实证文献都是以Fama的有效市场理论为基础，这一理论假设为：市场是有效的，价格行为遵循随机游走，价格之间是独立的并服从正态分布，投资者是完全理性的等等［1］。但越来越多的事实表明金融资产价格并不服从正态分布，而是具有簇族性和尖峰厚尾特征，价格之间也不是完全独立的，而是具有长程相关性，这些异常现象都难以用有效市场理论来解释。为此，经济物理学流派①该流派20世纪90年代兴起，它将物理学中的理论和方法应用到经济学系统中，从而产生经济物理学。提出了分形理论。分形理论的两个基本特征是自相似性和标度不变性，自相似性是指研究对象的组成部分以某种方式与整体相似的特性。标度不变性是指在一定的标度范围内，对被研究物体相应的测量结果不会随标度的改变而改变［2］30。Peters发现并分析了有效市场在理论上和实践中的不足，将混沌理论和分形理论应用于资本市场研究中［3］28－30［4］1－8。

近年来，分形理论以其非线性、自相似性、标度不变形、长记忆性等特点被广泛地用于金融时间序列的描述与刻画中，它打破原有金融经济学研究的线性范式，以全新的视角探索经济问题，以更为全面、细致、准确的方法描述价格波动特征，受到国内外学者的广泛关注。英国水文学家H.E.Hurst在考察尼罗河的水量变化时提出重标极差法（简称R／S），这是一种非常稳健的无参数统计方法［5］。Peters将此方法运用到资本市场研究中，发现Dow Jones和S＆P 500日、周、月、年之间的收益曲线具有分形特征。但此方法容易产生对短期记忆性或非平稳性时间序列相关性的误判。Peng和Buldyrev等在研究脱氧核糖核酸内部分子链相关性时，针对R／S分析法这一缺陷，提出了消除趋势波动分析方法 （简称DFA），该方法采用时间序列长程幂律相关性弥补了传统R／S方法对时间序列短程相关性的严格要求，一时间得到广泛的应用［6］。但大量实证研究表明目前资本市场的各分形局部结构呈现出非均匀一致的状况，一个分形维度已无法满足对分形结构的局部特征进行细致准确的刻画和描述，所以Kantelhardt和Zschiegner等通过将DFA方法与多重分形体系结合，改进DFA方法提出了MF－DFA方法［7］。Andreadis和Serletis等人分别运用MF－DFA分析法对日本证券市场和美国股票市场进行了分形研究，并得出了日本证券市场和美国股票市场具有多重分形特征的结论［8－9］。Gu等运用多重分形消除趋势波动分析方法证明1987—2008年美国WTI和欧洲Brent原油价格序列的多重分形结构特征的存在，并按两次海湾战争时间将样本区间分为3个子区间，比较分析三个阶段美国WTI和欧洲Brent原油市场的非线性特征［10］。Norouzzadeh等也借助MF－DFA分析法验证伊朗里亚尔兑美元汇率收益率的多重分形特征，证明长程相关性和厚尾分布是汇率收益率多重分形特征产生的主要原因［11］。

由于农产品期货价格是农产品价格的“晴雨表”，对农产品现货价格具有价格发现和规避风险的功能，所以对农产品期货市场分形特征进行研究，并对不同期货品种的多重分形程度进行比较分析，能够深入了解农产品期货价格波动的规律，为农业生产者、投资者和农产品消费者提供较为准确的远期价格信息，并有利于资产定价者和套利者有效地规避风险。目前国内已经有学者开始了这方面的研究。唐衍伟等利用修正的R／S分析方法，采集了近6年的市场交易数据，对中国农产品期货市场的分形特性和长程相关性进行了实证研究，证明大连黄豆期货市场存在状态持续性和波动积聚性，价格收益率时间序列呈现非线性特性［12］。李锬等选取郑州交易所九月份硬麦期货的日线、周线、月线数据，运用R／S分析法研究中国农产品期货价格波动的非线性和非周期循环长度［13］。何凌云根据大连豆一2000年7月17日至2007年9月26日价格的时间序列，采用R／S分析法通过定义q阶价格关联函数确认农产品期货市场的多重分形特征［14］。

但是，上述对农产品期货分形特征的研究均仅限于单一分形方法——R／S分析法，此方法只适合于稳定序列的分析，并且只能描述农产品期货市场的宏观面貌，无法对农产品期货市场的分形特征进行准确细致刻画［15］。为了更加准确细致地了解到中国农产品期货市场波动状况，并对未来波动和市场风险进行更为准确的预测和估算，本文运用多重分形消除趋势分析法（MF－DFA）和多重分形谱分析法从非线性的角度研究中国农产品期货市场的价格波动特征，比较强麦、硬麦、玉米、豆一四种代表性期货的多重分形强度的大小，并进一步探究造成中国农产品期货市场多重分形特征形成的原因。

二、研究方法

Kantelhardt提出了多重分形消除趋势波动分析（MF－DFA）方法，该方法是以时间序列每个分割区间上波动的平均值作为统计点，计算波动函数，再根据波动函数的幂律性确定广义Hurst指数，对平稳和非平稳序列结构及波动奇异性进行度量的一种多重分形分析方法。其优势在于能够发现非平稳时间序列中的长程相关性，并且能够避免对相关性的误判。

假设价格序列为P（i），i＝1，2，…，N，N表示时间序列的长度，MF－DFA计算方法如下：

步骤2 将序列｛y i｝Ni＝1分割成互不重叠的等长区间。对于任意正整数s，记Ns＝［N／s］，［x］表示x的整数部分。将序列｛y i｝Ni＝1自首向尾分成长度为s的N s个互不重叠的等长区间，由于N可能不是s的整数倍，为了不舍弃尾部剩余部分，将序列y i自尾向首再次重复上述过程划分一次，得到2Ns个区间：

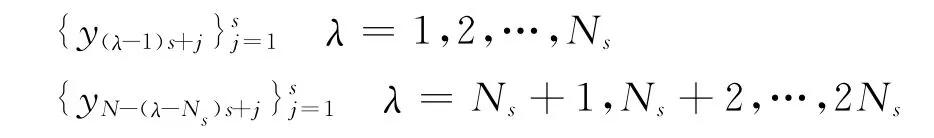
步骤3 通过拟合每一个子区间λ（λ＝1，2，…，2N s）上的m阶多项式趋势函数值，计算2N s个消除子区间局部趋势序列的平方均值：

步骤5 确定波动函数的标度指数，对于每一个确定的q值，存在幂律关系：

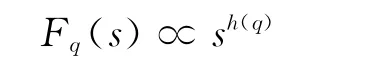
对每一个s，都可求出对应的Fq（s），做出lnFq（s）与lns的函数关系图，其斜率即为q阶Hurst指数h（q）。当h（q）随着q的变化始终为常数时，即时间序列每一小段消除趋势后的q阶波动相同，序列是单一分形，当h（q）为q的函数时，说明时间序列的局部结构非一致均匀，序列为多重分形。q＝2时的MF－DFA方法即为DFA方法，测算的h（2）就是经典的Hurst指数。当h（q）＞0.5时，时间序列呈现持续性特征，当h（q）＜0.5时，呈现反持续性特征，当h（q）＝0.5，时间序列服从随机游走。

步骤6 MF－DFA方法计算得到的h（q）与经典多重分形标度指数 ——Renyi指数τ（q）相关［7］：

步骤7 对式（5）进行Lengendre变换，得到多重分形谱两个重要指标——奇异指数α和多重分形谱f（α）［16］：

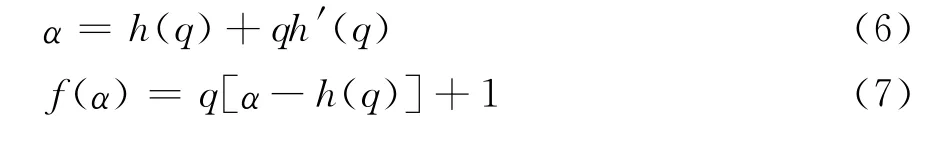
三、实证分析

（一）数据来源

选取大连和郑州商品交易所最活跃的四种期货价格时间序列数据，豆一和玉米数据分别选自大连商品交易所2002年7月15日至2010年11月12日和2004年9月22日至2010年11月12日的每日收盘价。强麦和硬麦分别选自郑州交易所2003年3月28日至2010年11月12日和1999年11月1日至2010年11月12日的每日收盘价，剔除节假日和缺失值，豆一、玉米、强麦和硬麦期货的样本数分别为1 963、1 492、1 810和2 448，数据均来源于wind数据库。

由于每个大宗商品期货合约的时间跨度都是有限的，任一合约在到期后都将不复存在，所以期货价格具有不连续性，并且同一交易日有若干个不同交割月份的期货在进行交易，所以同一交易日会同时存在同一品种的多个不同交割月的期货价格。为了产生连续的期货价格时间序列，对四种期货品种选取最近期月份的合约作为代表，当最近期合约进入交割期，选取下一个最近期的期货合约，如此滚动生成连续期货合约序列。

对期货价格计算对数收益率，期货价格日收益率rt定义为每日价格对数值的一阶差分：

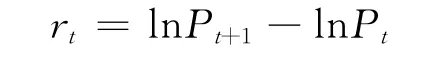
其中Pt为农产品期货在第t个交易日的交易价格，图1分别是强麦、硬麦、豆一、玉米四种农产品期货价格对数收益率rt随时间t变化的关系图。

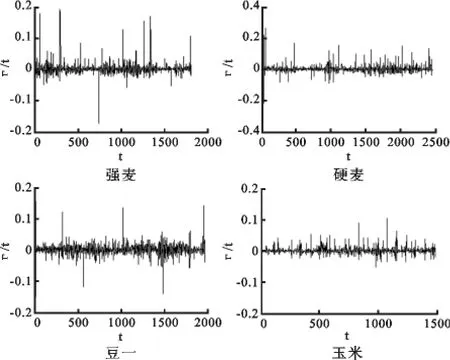
图1 四种农产品期货的rt－t图

从图1可以看出强麦、硬麦、豆一、玉米四种期货在样本区间内都存在多个异常波动的峰值。结合表1所示四种期货价格收益序列的基本统计量，可以看出，四种期货收益序列的偏度均不为0，峰度远远大于3，属于非正态分布。

表1 收益率序列的基本统计量表

（二）多重分形特征的实证分析

根据上述的MF－DFA分析法，本文分别对强麦、硬麦、豆一和玉米期货每日收盘价的收益率原始序列和变换后的收益率序列进行多重分形分析。在计算中s的取值范围为10～（N／6）天（N为时间序列总长度），笔者做出四种农产品期货收益率的lnFq（s）～lns图，研究发现各期货曲线自上而下，q值依次减少，对应的h（q）值逐渐增大；随着q的等差变化，相邻曲线的间距先由小变大，当q＜0时，又由大变小。说明随着q值取较大正数或是较小负数时，h（q）值逐渐收敛。因此，本文中q的取值范围选择［－5，5］，步长取0.1。q的取值范围选择［－5，5］，步长取0.1。从表2中可看出当多项式拟合阶数为3时，描述的波动更符合实际波动情况，所以分析时采用的数据和图形均为3阶多项式拟合结果。

从图2可看出，四种农产品期货收益序列的斜率均不为零，说明四种期货价格收益率序列不是简单的单一分形，而是多重分形。同样根据式（5）得到的Γ（q）～q图（图3）也可以看出四条Γ（q）～q曲线都是凸向横轴的，硬麦期货曲线的凸度和强麦相似，且略大于强麦，玉米次之，豆一最小，说明它们的多重分形强度也依次减弱。

由式（6）、式（7）得到多重分形谱f（α）～α（图4）。从图4也可以看出四种农产品期货的谱图f（α）～α呈钟形（单一分形的分形谱是一个点），钟型顶部较为平坦，底部开口宽大，说明农产品期货价格波动的振幅较大，价格波动的分布是非均匀分形结构。由于多重分形谱的谱宽可以作为衡量多重分形强度的一个指标，所以从各个图形的谱宽来看，硬麦的谱宽最大，随后依次是强麦、玉米、豆一，说明分形谱跨度依次减小，多重分形强度也随之逐渐减弱。

为了更加准确和深入地描述各种期货收益率的多重分形特征，根据方程式（1）～ （4），计算出四种期货在q＝－5、2、5处的Hurst值（见表2）。

图2 四种农产品期货收益率的h（q）～q图

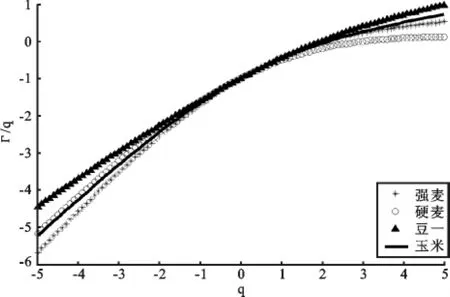
图3 四种农产品期货收益率的Γ（q）～q图

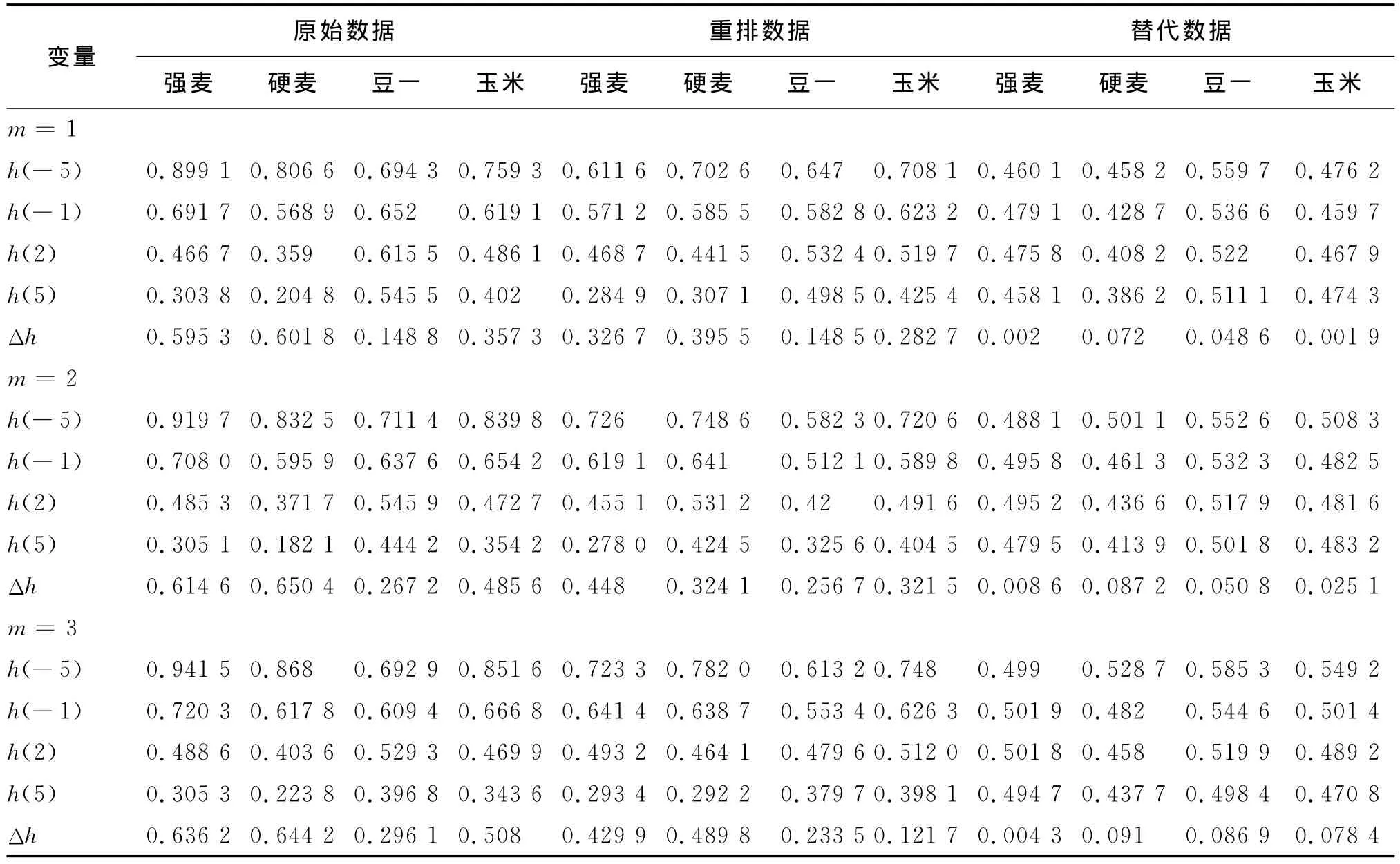
表2 收益率序列的h（q）值表

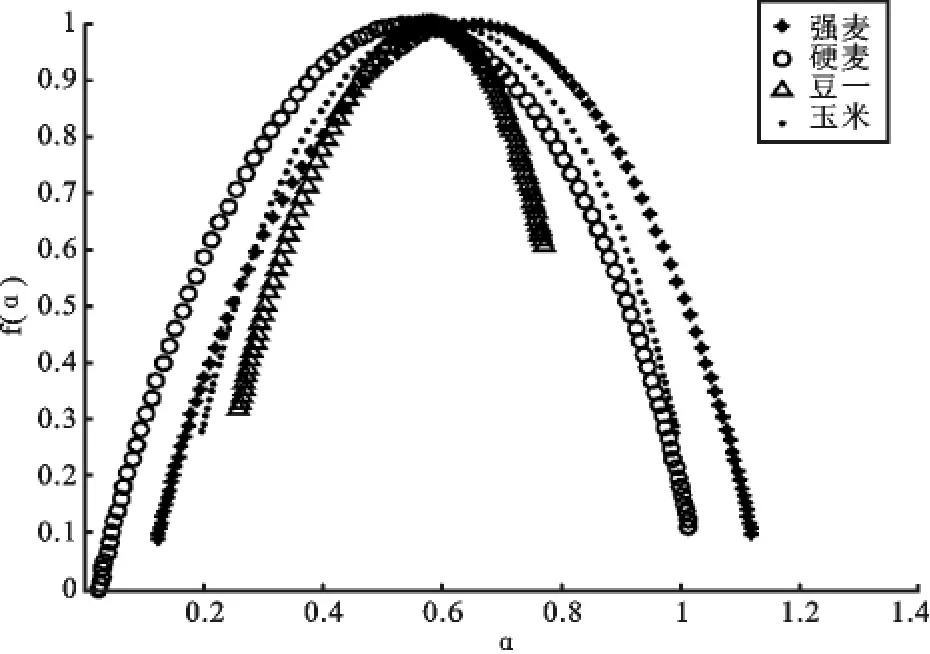
图4 四种农产品期货收益率的f（α）～α图

从表2中可以看出：

第一，当q从－5变化到＋5时，四种农产品期货收盘价的日收益率原始序列的h（q）均呈现递减趋势，且显著的不为常数，从定量的角度说明了四种农产品期货的收益率序列都存在显著的多重分形特征，不适合用单一分形模型来描述。而且，四种期货收益率原始序列的Hurst指数变化范围由大到小依次是硬麦、强麦、玉米、豆一，说明多重分形特征最强的是硬麦，最弱的是豆一，即相对而言硬麦的市场风险最大，豆一的风险最小。

第二，当q＝2时，强麦、硬麦、玉米期货收益率的经典 Hurst值分别为0.488 6，0.403 6，0.469 9，它们都显著地小于0.5，说明强麦、硬麦、玉米这三种期货的波动收益率具有长程相关性，并且这一相关性呈现出反持续性，也就是说强麦、硬麦、玉米期货未来收益率的变动和现在收益的变动呈负相关。而豆一的Hurst值大于0.5，呈现持续相关性，即某一时段豆一期货向上的收益变动也会跟随有下一段豆一期货收益的向上变动。

第三，结合波动函数的特点，以h（q）＝0.5为分界点，当q≤－1时，即q为较小负数时，硬麦、强麦、玉米、豆一期货的 Hurst指数h（q）＞0.5，此时四种农产品期货收益率的小幅波动影响被放大，收益率序列呈现持续性特征，突出市场内在因素的作用，即市场供给等内部因素导致硬麦、强麦、玉米、豆一期货收益在一段时间内呈现持续向上或是向下的变动。当q＞2时，即q为较大正数时，Hurst指数h（q）＜0.5，此时农产品期货收益率的大幅波动影响被放大，收益率序列呈现反持续性特征，说明市场外在因素的作用会导致硬麦、强麦、玉米、豆一期货收益向上向下的交替变动，这一实证结果也与现实情况相吻合。

（三）多重分形特征的成因分析

通常时间序列的多重分形性有两种解释：一种是由大幅波动和小幅波动的长程相关性不同造成。另一种是由波动的厚尾概率分布引起。对原始数据进行重排能保留时间序列的波动分布，却破坏了它的相关性，而相位随机化处理可以弱化时间序列的非高斯分布，同时保留收益率的相关关系。所以，通过对原始数据的重排和相位随机化处理可以有效区分两种原因对多重分形的贡献程度。

比较表2中硬麦、强麦、豆一和玉米期货的重排数据、替代数据与原始数据的分析结果，可以看出经过重排处理后的收益序列的广义Hurst值h（2）分别为0.493 2、0.464 1、0.479 6、0.512 0，替代数据的广义 Hurst值h（2）分别为 0.501 8、0.458、0.519 9、0.489 2，都更接近于0.5，但都不等于0.5，说明收益序列的非正态分布和长程相关性以及其他一些潜在因素共同导致了多重分形特征的形成。但替代数据的h（q）的变化值分别为0.004 3、0.091、0.086 9、0.078 4，接近于零并远远小于原始数据的Δh值，同时也小于重排数据的Δh值，这一结果表明硬麦、强麦、玉米和豆一期货的收益序列分布是导致其多重分形性形成的主要原因。

四、结 论

本文运用多重分形消除趋势波动分析法（MF－DFA）和多重分形谱分析法，对中国农产品期货市场的四种主要农产品期货——强麦、硬麦、豆一和玉米价格收益进行实证研究，得到如下结论：

第一，传统有效市场理论不适合农产品期货市场波动规律的研究。有效市场理论建立在资产价格服从正态分布和价格之间相互独立的假设基础之上，但本文实证研究发现农产品期货市场四种具有代表性期货的收益率的Hurst指数均不等于0.5，说明农产品期货价格波动不服从随机游走过程，而是表现为分形分布的特征，所以传统有效市场理论已经不适合农产品期货市场波动规律的研究。

第二，农产品期货价格体系具有多标度特性，Hurst指数h（q）和Renyi指数Γ（q）都随着阶数q的变化而变化说明农产品期货市场存在多重分形特征。因此，用单一分形法（R／S）和DFA研究农产品期货市场非线性特征具有一定的局限性，采用多重分形的方法来进行分析更为合适。

第三，强麦、硬麦、玉米三种期货的收益具有长程相关性，并且这一相关性呈现出反持续性，而豆一期货呈持续相关性。相对于强麦、玉米、豆一期货而言，硬麦期货具有更强的长程相关性和更大的奇异谱宽度，硬麦、强麦、玉米、豆一期货的多重分形强度依次减弱，也说明了它们的市场风险程度依次减弱。

第四，四种期货价格收益率呈多重分形特征是由长程相关性和非正态分布以及信息传播不对称、投资者行为受限、市场不成熟等其他潜在因素共同造成的，其中非正态分布在四种期货的多重分形特征形成过程中起主导作用。

［1］ Fama E F.Efficient Capital Markets：a Review of Theory and Empirical Work［J］.Journal of Finance，1970，25（2）.

［2］ Mandelbrot B B.The Fractal Geometry of Nature［M］.New York：W H Freeman，1982.

［3］ Peters E.Fractal Market Analysis：Applying Chaos Theory to Investment and Economics［M］.New York：John Wiley＆Sons，Inc.，1994.

［4］ Peters E.Chaos and Order in Capital Markets：a New View of Cycles，Prices and Market Volatility［M］.2rd ed.New York：John Wiley＆Sons，Inc.，1996.

［5］ Hurst H E.Long Term Storage Capacity of Reservoirs［J］.Transactions American Society of Civil Engineers，1951（1）.

［6］ Peng C K，Buldyrev S V，Havlin S.Mosaic Organization of DNA Nucleotides［J］.Physical Review E，1994，49（2）.

［7］ Kantelhardt J W，Zschiegner S A，Koscienlny Bunde E.Multifractal Detrended Fluctuation Analysis of Nonstationary Time Series［J］.Physica A，2002（1／4）.

［8］ Katsuragi H.Evidence of Multi－affinity in the Japanese Stock Market［J］.Physica A，2000（1／2）.

［9］ Serletisa.Evidence of a Random Multifractal Turbulent Structure in the Dow Jones Industrial Average［J］.Chaos，Solitons and Fractals，2002，13（6）.

［10］Gu Rongbao，Chen Hongtao，Wang Yudong.Multifractal Analysis on International Crude Oil Markets Based on the Multifractal Detrended Fluctuation Analysis［J］.Physica A，2010，389（14）.

［11］Norouzzadeh P，Rahmani B.A Multifractal Detrended Fluctuation Description of Iranian Rial－US Dollar Exchange Rate［J］.Physica A，2006（2）.

［12］唐衍伟，陈 刚，张晨宏.中国农产品期货市场价格波动的长程相关性研究［J］.系统工程，2005（12）.

［13］李锬，李鹏，齐中英.农产品期货价格时间序列 R／S分析［J］.商业研究，2006（5）.

［14］何凌云，周曙东.中国农产品期货价格的分形和多重分形特征［J］.中国农学通报，2008（3）.

［15］都国雄，宁宣熙.上海证券市场的多重分形特性分析［J］.系统工程理论与实践，2007（10）.

［16］Koscielny B E，Kantelhardt J W，Braun P.Multifractal of River Runoff Records：Detrended Fluctuation Studies［J］.Journal of Hydrology，2006，322（1／4）.

An Analysis on Features and Causes of Multi－Fractal in China＇s Agricultural Futures Markets

LI Zhi-hui，LU Xin-sheng

（School of Economics and Management，Northwest A＆F University，Yangling 712100，China）

By means of Multi－fractal Detrended Fluctuation Analysis（MF－DFA）and multi－fractal spectrum analysis，this paper analyzes the time series of four major agricultural futures prices in China＇s agriculture futures markets.It finds that there are multi－fractal characteristics in China＇s agricultural futures markets.Furthermore，multi－fractal spectrum shows that stronger long－range correlation and wider spectrum exists in hard wheat price market.And there are two different types of sources for multifractal characteristics in time series，namely，fat－tailed probability distributions and nonlinear temporal correlations.Multi－fractal characteristics of time series in China agricultural futures markets are mostly due to non－Gaussian distribution correlations.

agricultural futures；multi－fractality；MF－DFA；multi－fractal spectrum；longrange correlation

（责任编辑：李 勤）

F832.1

A

1007－3116（2011）10－0084－06

2011－05－08

李志慧，女，湖北荆门人，博士生，研究方向：金融工程和金融市场复杂性；

卢新生，男，陕西洛南人，教授，博士生导师，研究方向：国际金融市场波动、金融工程和货币政策。

【统计理论与方法】