高凝油井筒温度场计算及流态转变分析

姚传进 雷光伦 蒋宝云 刘海庆

（1.中国石油大学石油工程学院，山东青岛 266555；2.中国石化胜利油田鲁明油气勘探开发有限公司，山东东营 257000）

高凝油油藏在世界上分布较广，国内辽河、吉林、大港、河南、胜利等油田都有相当储量的高凝油油藏［1］。由于高凝油含蜡量高、凝固点高，在生产过程中随着温度、压力的降低以及原油中轻组分的逸出，蜡开始结晶析出，并在井筒内沉积，油井经常因油稠、结蜡、负荷过重而出现抽油杆卡死、断脱等不能正常生产的现象，开发成本高，开采效果差。开展高凝油井筒温度场计算及流态转变分析，可得到油井在不同产量下的结蜡深度和原油流动阻力大幅度增加（流态转变）时的控制条件，是确定合理的采油工艺，进行高凝油藏顺利开发的重要保障。笔者基于传热学及两相流理论，建立了适合高凝油井的井筒温度场计算模型，并计算了普通油管和隔热油管井的井筒温度场；通过实验研究了高凝油的黏温特性，进而结合实验现象和计算结果，对垂直井筒中高凝油的流态转变进行了分析。

1 井筒温度场计算数学模型

1.1 模型建立

1.1.1 假设条件 为了简化复杂的井下情况，作如下假设［2-4］：（1）油井以定产量生产；（2）井筒到水泥环外缘间的传热为一维稳态传热，水泥环外缘到地层间的传热为一维非稳态传热，且不考虑沿井深方向的传热；（3）忽略地层导热系数沿井深方向的变化；（4）井筒管柱材料、结构、尺寸、热物理性质均匀一致；（5）动液面以上环空介质均匀分布，并且热物理性质不随压力下降而变化；（6）地层原始温度为线性变化，地温梯度已知；（7）圆筒井壁。物理模型如图1所示。

图1 井筒管柱结构

1.1.2 井筒传热数学模型 根据传热学与能量平衡原理，在井筒上任意取长度为dl的微元段，则井筒微元的能量平衡方程为

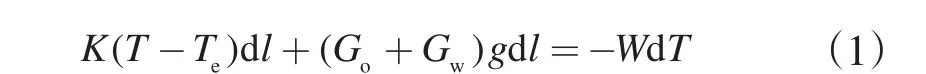
边界条件：l=0，T=T0。

式中，K为产液与地层间单位管长的总传热系数，W/（m·℃）；T为井筒原油温度，℃；T0为油层中部温度，℃；Te为地层温度，℃；l为从井底至井中某一深度的垂直距离，m； Go、Gw为产出原油和水通过油管的质量流量，kg/s；（Go+Gw）gdl为产液的举升功，可忽略不计；g为重力加速度，m/s2；W=GoCo+GwCw为水当量，W/℃；Co、Cw分别为产出原油和水的比热，J/（kg·℃）；dl为井筒微元段长度，m；dT为井筒微元段的温度变化，℃。

（1）油管中心至水泥环外缘的稳态传热。根据稳态传热学原理［5］得

式中，Th为水泥环外缘处的温度，℃；dQ为井筒微元段的热流速度，W；Kl为井筒到水泥环外壁间单位管长的传热系数，W/（m·℃）。

（2）水泥环外缘至地层的非稳态传热。当水泥环外缘温度一定时，随着时间的变化，地层中同一位置的温度逐渐升高，径向温升前缘逐渐增加［6］，地层中的非稳态导热可表示为

式中，λe为地层导热系数，W/（m·℃）；tD为地层导热时间函数，无因次；m为地温梯度，℃/100 m。

1.1.3 井筒传热系数计算 井筒传热过程如图2所示。

图2 井筒—地层传热示意图

可以看出，井筒传热热阻包括：油管内壁对流换热热阻（Ro）、油管导热热阻（Rtub）、环空自然对流和辐射换热热阻（Rtc）、套管导热热阻（Rcas）、水泥环导热热阻（Rcem）和地层热阻（Re）。根据圆筒壁传热原理［7］，各传热热阻为

式中，Ro、Rtub、Rtc、Rcas、Rcem、Re依次为油管内壁对流换热热阻、油管导热热阻、环空自然对流和辐射换热热阻、套管导热热阻、水泥环导热热阻、地层热阻，（m·℃）/W；rti为油管内径，m；rto为油管外径，m；rci为套管内径，m；rco为套管外径，m；rh为水泥环半径，m；hf为油管内壁对流换热系数，W/（m2·℃）；λtub为油管的导热系数，W/（m·℃）；λcas为套管的导热系数，W/（m·℃）；λcem为水泥环的导热系数，W/（m·℃）；hc、hr分别为油套环空的对流换热系数和辐射换热系数，W/（m2·℃）。

Ramey 定义了地层导热时间函数tD的经验表达式［8］

式中，α为地层热扩散系数，m2/s；t为加热时间，h。

求得各个热阻，便可计算产液与地层间单位管长的总传热系数K、井筒到水泥环外壁间单位管长的传热系数Kl

1.2 模型求解

计算井筒温度分布要用到流体物性参数和流动参数，而流体物性参数和流动参数与压力有关，要计算井筒压力降就必须对垂直井筒动态作深入分析。国内外有关学者建立和发展了许多综合各种不同气液两相流相关式的井筒动态预测模型［9］。Lawson—Brill计算比较指出，Orkiszewski相关式的计算结果比较接近实测值［10］。所以本研究采用Orkiszewski的两相流动压力降的计算方法求解井筒中的压力分布。计算步骤如下：（1）给定井身结构及相关热物理性质参数；（2）选取合适的微元段，已知微元段下端的深度Hin、温度Tin、压力pin，假设计算段长度∆h，假设微元段上端的温度Tout1、压力pout1；（3）计算微元段的平均温度Tav和平均压力pav，并求得此时流体全部物性参数；（4）计算微元段的各个换热系数和环空当量导热系数；（5）计算油、套管的壁温，计算产液的水当量，计算微元段的上端温度Tout2；（6）计算微元段相应的流型界限，并确定流动型态；（7）按流型计算微元段流体的平均密度及摩擦梯度；（8）计算对应于∆h的压力降∆p，从而得微元段的上端压力Tout2=pin−∆p；（9）如果Tout2小于原油凝固点，差值计算油井结蜡深度，并输出计算结果；（10）如果| Tout1−Tout2|＜ε1、| pout1−pout2|＜ε2，则该微元段温度场计算完毕，进入下一微元段计算；否则，令Tout1=（Tin+Tout2）/2、pout1= （pin+pout2）/2转步骤③；如此继续下去，直到计算到井口为止。

2 井筒温度场计算结果与分析

2.1 高凝油井筒温度场计算

利用所建立的井筒温度场数学模型，以疃3块3口为例进行了计算，疃3块3口井的基本生产参数及计算结果见表1和图3。

表1 疃3块3口井的基本生产参数

图3 疃3块3口井的井筒温度场曲线

可以看出：井口温度的计算误差低于5%，结蜡深度的计算误差低于10%，所建立的数学模型具有较高的计算精度，满足现场的需要，可用于高凝油井井筒温度场的准确预测。在目前的生产参数下，3口油井结蜡严重，结蜡深度分别为448 m、462 m、492 m，均无法正常生产。其中，油井3-X1的井口温度最高及结蜡深度最小，原因在于水的比热比油大，散失相同的热量时，水降低的温度较小，即高含水率对原油具有一定的保温效应；油井3-X4的井口温度最低及结蜡深度最大，原因在于该井的产量较低，举升同样的高度，散失的热量较多，即高产液量有利于高凝油井筒温度的保持。

2.2 隔热油管井的井筒温度场计算

理论上讲，增大传热热阻中的任一部分都可以达到增大总传热热阻、削弱井筒传热的目的。结合油田现场的实际情况，采用隔热油管可以有效地增大油管部分的传热热阻，进而增大传热总热阻、削弱井筒传热。而且，目前油田用隔热油管已经系列化和标准化，现场应用相当方便。

我国的石油天然气行业标准给出了预应力隔热油管的相关标准（SY/T 5323—94［11］），隔热油管按其导热系数分为5个等级，导热系数分别为：A级 0.08~0.06 W/（m·℃）；B级0.06~0.04 W/（m·℃）；C级0.04~0.02 W/（m·℃）；D级0.02~0.006 W/（m·℃）；E级0.006~0.002 W/（m·℃）。

应用所建立的数学模型，计算了隔热油管条件下疃3块3口高凝油的井筒温度场。图4为不同油管导热系数下3-X1井的井口温度变化曲线，图5为不同油管导热系数下3-X1井的井筒温度分布曲线。

图4 不同油管导热系数下3-X1井的井口温度变化

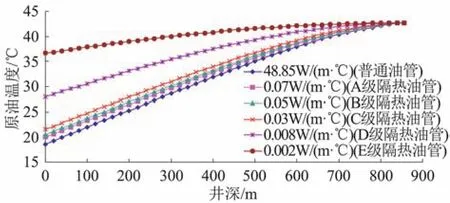
图5 不同油管导热系数下3-X1井的井筒温度分布曲线

可以看出：采用较低导热系数的隔热油管可有效削弱井筒传热；对3-X1井而言，当油管的导热系数高于0.01 W/（m·℃）时，井口原油温度变化幅度不大，而当油管的导热系数低于0.01 W/（m·℃）时，井口温度随导热系数的减小呈现出直线增加的变化趋势，井筒温度分布曲线离地层温度分布曲线也越来越远。当井口原油温度高于原油凝固点33℃时，即可实现高凝油井正常生产，此时3口高凝油井采用的隔热油管导热系数依次为0.0034 W/（m·℃）、0.0033 W/（m·℃）、0.0030 W/（m·℃），均为E级隔热油管。

3 高凝油流动性实验与分析

为了计算高凝油井的结蜡深度，采用GB/ T510-83测定了高凝油油样（取自潍北油田疃3块孔二段）的凝固点。然后，在温度分别为凝固点、35℃、40 ℃、45 ℃、50 ℃、55 ℃和60 ℃条件下，利用旋转黏度计测定了高凝油样在不同剪切速率（20 s-1、40 s-1、60 s-1、80 s-1、100 s-1、200 s-1、400 s-1、800 s-1）下的黏度，观察了原油流态的变化。由实验所得数据绘制油样在不同剪切速率下的黏温曲线，曲线上的两个折点对应高凝油的析蜡点和反常点。根据凝固点、反常点和析蜡点并结合实验现象，可对高凝油井的流态转变段进行计算和分析。

图6为实验得到的潍北油田疃3块高凝油黏温特性曲线，可以看出：高凝油的流动性对温度极其敏感，其黏温关系呈三折线式特征，两折点对应温度分别为高凝油的析蜡点（45 ℃）和反常点（38 ℃）。

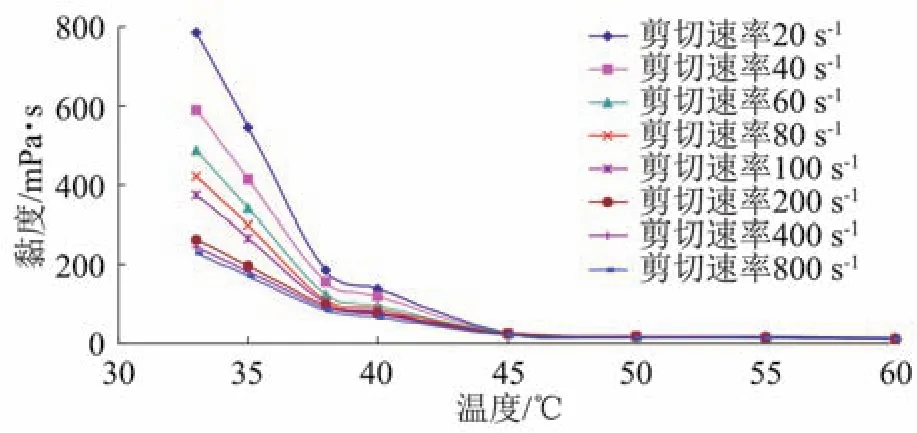
图6 两组油样在不同剪切速率下的黏温关系

实验测得潍北油田疃3块高凝油的凝固点为33 ℃。以析蜡点、反常点和凝固点为分界点，将垂直井筒中高凝油的流态划分为4种，其转变位置可利用高凝油井筒温度场数学模型计算得到。

综合分析高凝油的黏温特性曲线、流态转变位置的计算结果及观察到的实验现象（图6、表2）可知：垂直井筒中高凝油出现如下流态转变特征。

（1）当原油温度高于45 ℃时，高凝油为单一液态。原油黏度较低，且黏温关系基本与剪切速率无关，呈现出与普通原油相同的牛顿流体特征，具有较好的流动能力。这是因为当原油温度高于原油析蜡点时，蜡全部溶于原油中。

（2）当原油温度介于38 ℃和45 ℃之间时，高凝油为悬浮液态。蜡从高凝油中析出，并高度悬浮分散于原油中，形成原油为连续相、蜡为分散相的双相体系；原油黏度缓慢上升，黏温关系与剪切速率有关，因其黏度受剪切速率影响较小，仍可近似看作牛顿流体。这是因为温度降低，蜡在原油中的溶解度下降，当原油温度降至析蜡点时，少量蜡结晶析出，且蜡晶尺寸较小，可悬浮分散于原油中。

（3）当原油温度介于33 ℃和38 ℃之间时，高凝油为海绵状凝胶体态。原油黏度急剧增加，黏温关系受剪切速率的影响显著，低剪切速率条件下黏度更高，呈现出非牛顿流体特征和轻微的触变性特征，具有剪切稀释性。这是因为原油温度降至反常点时，由于析出的蜡晶增多并缔结，且具有一定的结构强度 。

（4）当原油温度低于33 ℃时，高凝油为触变性固体态。高凝油失去流动性，发生“凝固”，在较低的扭矩下，流变仪的转子无法正常转动；具有屈服假塑性流体的流变特征，并同时呈现明显的触变性，为触变性假塑性流体。原因在于：当原油温度低于凝固点后，蜡晶相互连接形成空间网络结构，成为连续相，液态烃则被隔开而成为分散相，由于空间网络结构具有较高的结构强度，致使流变仪无法正常转动，若使原油流动，则务必施加一外力克服这一强度。

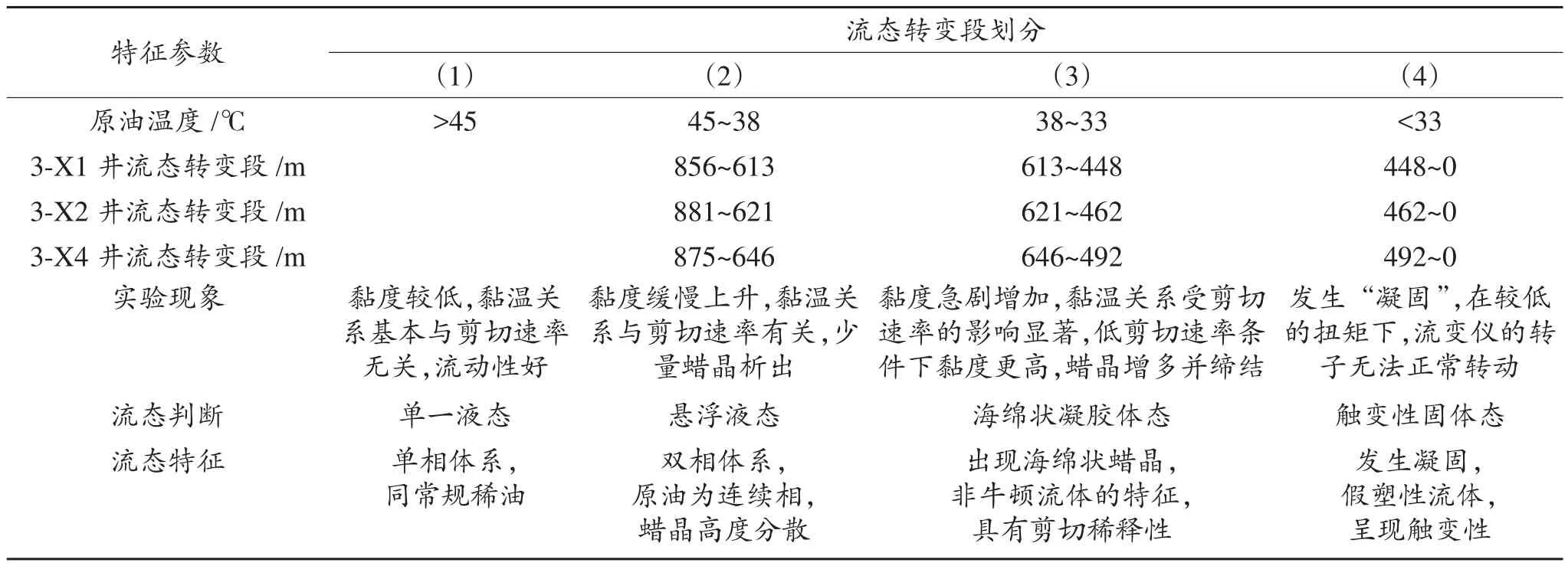
表2 疃3块3口井原油的特征温度及流态转变分析

对于较深的高凝油井（油层中部温度高于原油的析蜡点），在整个井筒举升过程中，原油依次出现上述4种流态；由于疃3块3口高凝油井较浅，油层中部温度低于原油的析蜡点，因此均不存在单一液态；在整个井筒举升过程中，原油依次出现悬浮液态、海绵状凝胶体态和触变性固体态，经历2次流态转变；每经过一次流态转变，原油黏度就会明显增加一次；当原油温度下降到凝固点后，其黏度急剧增加，并发生凝固，转变为触变性固体态，流动阻力也大幅度增加，此即为高凝油井无法正常生产的内在原因。

4 结论

（1）所建立的数学模型具有较高的计算精度，井口温度的计算误差低于5%，结蜡深度的计算误差低于10%，满足现场的需要，可用于高凝油井井筒温度场的准确预测；在目前的生产参数下，潍北油田疃3块3口高凝油井结蜡严重，结蜡深度分别为448 m、462 m、492 m，均无法正常生产；高含水率和高产液量有利于高凝油井筒温度的保持；当潍北油田疃3块3口分别采用导热系数为0.0034 W/（m·℃）、0.0033 W/（m·℃）、0.0030 W/（m·℃）的E级隔热油管，可实现正常生产。

（2）高凝油对温度十分敏感，其黏温关系呈三折线式特征；与此对应，在整个井筒举升过程中，自下而上高凝油从单一液态→悬浮液态→海绵状凝胶体态→触变性固体态进行流态转变；当油温下降到凝固点后，原油黏度急剧增加，并发生凝固，转变为触变性固体态，流动阻力也大幅度增加，此即为高凝油井无法正常生产的内在原因。

［1］ 彭轩，刘蜀知，蔡长宇，等.高凝油油藏自生热压裂井筒温度场计算模型［J］.石油学报，2003，24（4）：69-76.

［2］ 任瑛，梁金国，杨双虎，等.稠油与高凝油热力开采问题的理论与实践［M］.北京：石油工业出版社，2001：4-24.

［3］ 王庆，吴晓东，刘长宇，等.高含CO2原油井筒流动压力和温度分布综合计算［J］.石油钻采工艺，2010，32（1）：65-69.

［4］ 李启堂，王立影，何东升，等.基于集肤效应的空心抽油杆电热系统的数值计算［J］.石油学报，2005，26（3）：110-113.

［5］ 陈月明.注蒸汽热力采油［M］.山东东营：石油大学出版社，1996：64-84.

［6］ 刘慧卿，范玉平，赵东伟，等.热力采油技术原理与方法［M］.山东东营：石油大学出版社，2000：30-34.

［7］ 戴锅生.传热学［M］.第2版.北京：高等教育出版社，2006：31-34.

［8］ HASAN A R, KABIR C S.Heat transfer during two phase flow in wellbores: Part1-formation temperature.［R］. SPE 22866, 1991.

［9］ 朱炬辉，胡永全，赵金洲，等.相态变化影响下的凝析气井井筒压力变化计算分析［J］.大庆石油地质与开发，2006，25（6）：50-53.

［10］ 陈家琅.石油气液两相管流［M］.北京：石油工业出版社，2005-12：27-59.

［11］ 赵正琪，王弥康，张毅，等.SY/T 5324—94 预应力隔热油管［S］.北京：石油工业出版社，1995.