潮汐调和分析方法的探讨

张凤烨, 魏泽勋 , 王新怡, 王永刚, 方国洪

(1. 海洋环境科学与数值模拟国家海洋局重点实验室, 山东 青岛 266061; 2. 国家海洋局 第一海洋研究所,山东 青岛266061)

潮汐调和分析方法的探讨

张凤烨1,2, 魏泽勋1,2, 王新怡1,2, 王永刚1,2, 方国洪1,2

(1. 海洋环境科学与数值模拟国家海洋局重点实验室, 山东 青岛 266061; 2. 国家海洋局 第一海洋研究所,山东 青岛266061)

为实现对不等时距潮汐资料的分析, 基于 Matlab内部函数功能, 提出了一种调和分析方法。基于这种方法, 分别对大连、北海两个站位1985年的全年等时间间距取样的资料和非等时间间距取样的资料进行了调和分析, 结果显示, 由等时间距资料和非等时间距资料计算的调和常数基本吻合。对大连、北海两个站位的全年资料进行多个不同时间间距取样分析, 发现当分潮频率大于取样频率的二分之一时, 分潮发生频率混淆。若分潮周期明显大于样品长度, 该分潮的分析结果产生很大误差。最后得出结论为： 此调和分析方法, 适合对非等时间间距、非连续潮汐潮流资料进行调和分析, 并且能够获得与传统方法精度相当的结果。

Matlab; 潮汐; 调和分析; 取样

在实际的海洋调查中, 尤其是长时间的观测,由于受到仪器故障、恶劣天气、地理位置制约, 观测方式等因素的影响, 很难得到从观测初始时刻到结束时刻这段时间内完整的高质量数据资料, 也可以说获得的海洋资料是不完整的、不连续的。对于潮汐资料, 调和分析方法作为一种主要的分析方法,发展至今, 理论基础已经很成熟, 但是传统的调和分析大多是对观测时间间隔为等距的资料进行调和分析, 这是由于非等时序列数据的法方程系数矩阵很大, 所需的计算量也非常大, 通常要求观测数据等时间间隔以减少计算量, 而且常用的观测资料也是以观测时间间隔为等距离为主。若资料中出现数据缺测漏测, 或者因为异常天气和其他原因使得部分实测数据相对正常潮汐存在大的误差, 就首先要对数据进行前期处理[1], 然后应用最小二乘法对潮汐进行调和分析, 这种方法在计算时, 首先将原始矛盾方程进行求导处理, 从而得到矛盾方程的法方程, 这样大大增加了计算的难度[2]。如果我们从线性代数这门学科的角度来考虑, 矛盾方程组只是一个线性代数中的超定方程组, 只需要直接解这个超定方程组即可, 基于 Matlab内部函数功能求解线性方程组能很好地解决这一问题, 并且方程组所得解即为最小二乘解[3-4], 从而简化了调和分析的算法。有多少样本, 就有多少个方程, 更能体现最小二乘法的灵活性, 完全不受等时或非等时取样的限制。

本文采用基于Matlab内部函数功能的最小二乘法实现潮汐资料的调和分析, 并应用于大连、北海两站位的水位观测资料分析, 通过对两站位全年资料的调和分析, 从非理论推导的角度, 分析基于Matlab内部函数功能的调和分析方法是否可应用于等时间间隔和不等时间间隔的观测资料的调和分析,以及观测资料的取样间隔对于调和分析精度的影响,然后通过对两站位 7月份资料的调和分析, 来分析采样长度对潮汐调和分析精度的影响。

1 改进的潮汐调和分析方法介绍

调和分析是建立在分潮的概念上[5], 将潮汐看成是以不同频率传播的各种潮波叠加产生的现象,调和分析的目的就是求出各个分潮的振幅和迟角,迟角是指： 某时刻、某一地点实际的分潮的相角与理论上该时刻的分潮相角的差值, 迟角分为3种： 有区时迟角、地方迟角、格林威治迟角。现在国际上通用的是格林威治迟角, 用字母g表示, 本文所用的迟角即为格林威治迟角[6]。

潮位表示式如下：

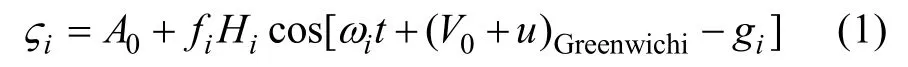
式中A0为平均水位高度,i为分潮序列号,ζ表示分潮潮高,ω为分潮的角速度,f,u分别表示由于月球轨道18.61 a的周期变化引进的对平均振幅H和相角的订正值, 即交点因子和交点订正角,V0为格林威治初相角,H和g为分潮的调和常数。

本文利用潮位公式, 建立一种基于 Matlab内部函数功能的潮汐调和分析方法, 其区别于传统的调和分析方法, 其特殊之处在于, 这种基于 Matlab内部函数功能的调和分析方法可以对不等时间间隔的潮汐、潮流资料进行调和分析, 而且计算易于实现。下面将介绍这种基于Matlab内部函数功能的潮汐调和分析的方法和原理。

设有观测资料：ζ(j),j=1,2,3…N,N代表数据个数, 该资料每∆t小时为一次记录, 此处的∆t既可以是整数, 也可以是小数或者是一个不定值。取数据的开始时刻为时间原点。

设潮汐为M个分潮叠加而成：

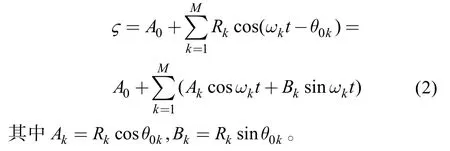
由于每个分潮的ω是一个定值, 所以每个时刻的cosωt, sinωt是一个常数, 这里A0是平均水位,我们可以把它看做是ω为0的一个分潮。这样就形成了一个有2M+1个未知量的方程个数为N的线性方程组, 然后应用基于 Matlab的内部函数功能的最小二乘法, 直接对线性方程组进行求解, 从而得最小二乘解, 即每个对应分潮的A,B。

每个分潮的ω根据下式求得：

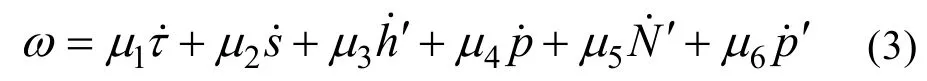
通过 Matlab可以求出一个平均水位、N/2个A值和N/2个B值。根据得出各分潮的振幅和相位。最后只要依据天文要素计算出初始时刻的f,u和V0, 此处f,u和V0为格林威治时刻值。根据即可求出调和常数, 其中f,u的计算方法参照引潮力的第四展开式[1,8]。

2 站点水位的潮汐调和分析

下面将采用基于Matlab内部函数功能的潮汐调和分析方法对大连、北海两个站点等间隔资料、非等间隔资料以及不同时距的等时间隔进行调和分析,讨论本方法的适用性以及适用条件。

2.1 1 a资料的调和分析

利用基于Matlab内部函数功能的调和分析方法对两个站点的1 a的水位资料进行调和分析, 从潮族中选取具有代表意义的分潮, 选取了 30个分潮, 分别为 K1, O1, Q1, P1, MP1, J1、SO1, OO1, M1, M2, S2, N2,K2, OQ2, L2, O3, MO3, K3, MK3, M4, MS4, Mk4, SN4,2MK5, MSK5, M6, MSk6, 2Mk6, Sa, Ssa。

分别对大连、北海1 a(1985年)的观测资料进行调和分析, 这里原始观测数据取样的时间间隔是1 h, 而对于非等时的观测资料的分析, 首先对原始数据进行处理, 去掉 3月份的所有的观测资料, 然后随机删除一些水位观测资料, 使其达到一种非等时距采样的效果, 然后对其进行调和分析, 从图 1可以看到, 等时调和分析预报的结果和不等时调和分析预报的结果与原始的观测资料基本上是重合的, 从表1、表2可以看出, 等时间序列调和分析得到的调和常数与非等时间序列的调和常数的值非常接近, 表中提到的原始值代表的是利用传统的调和分析方法对潮汐观测数据进行调和分析所得的调和常数, 由于本文中提到的原始调和常数是对26 a数据进行调和分析由135个分潮所得, 所以一些分潮的调和常数与本文计算的调和常数有一定的差别, 如因为M1分潮的杜德森数自身的问题, 所以其调和常数不予考虑, 但是主要分潮的调和常数与本文计算所得分潮调和常数相当接近。这说明基于 Matlab内部函数功能的调和分析方法适用于潮汐资料的调和分析。

下面的实验主要是探讨数据的取样间隔对该方法所得调和常数的影响, 为了从结果上讨论取样频率是否对基于Matlab内部函数功能的调和分析方法有影响, 本文分别对大连、北海两站位时长为1 a、取样时间间隔分别为1, 2, 3, 4, 5, 6 h的观测数据, 应用基于Matlab内部函数功能的调和分析方法进行调和分析, 然后对调和常数进行对比, 结果见表 3、表4、表 5、表 6。

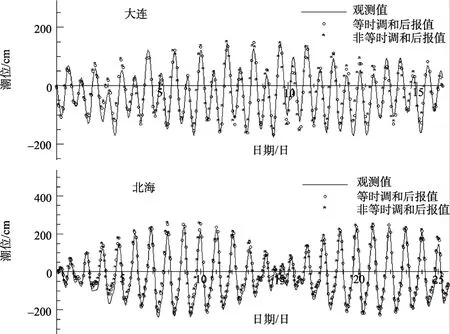
图1 1985年1月大连、北海潮位观测数据、等时和非等时后报值图Fig. 1 The chart of tide values, showing the observational and the hindcast values of harmonic analysis of data sampled at equal time intervals and non-equal time intervals in Dalian and Beihai in January 1985

表1 大连原始、等时与不等时资料调和常数比较Tab. 1 The comparison of harmonic analysis of data sampled at equal time intervals and non-equal time intervals in Dalian

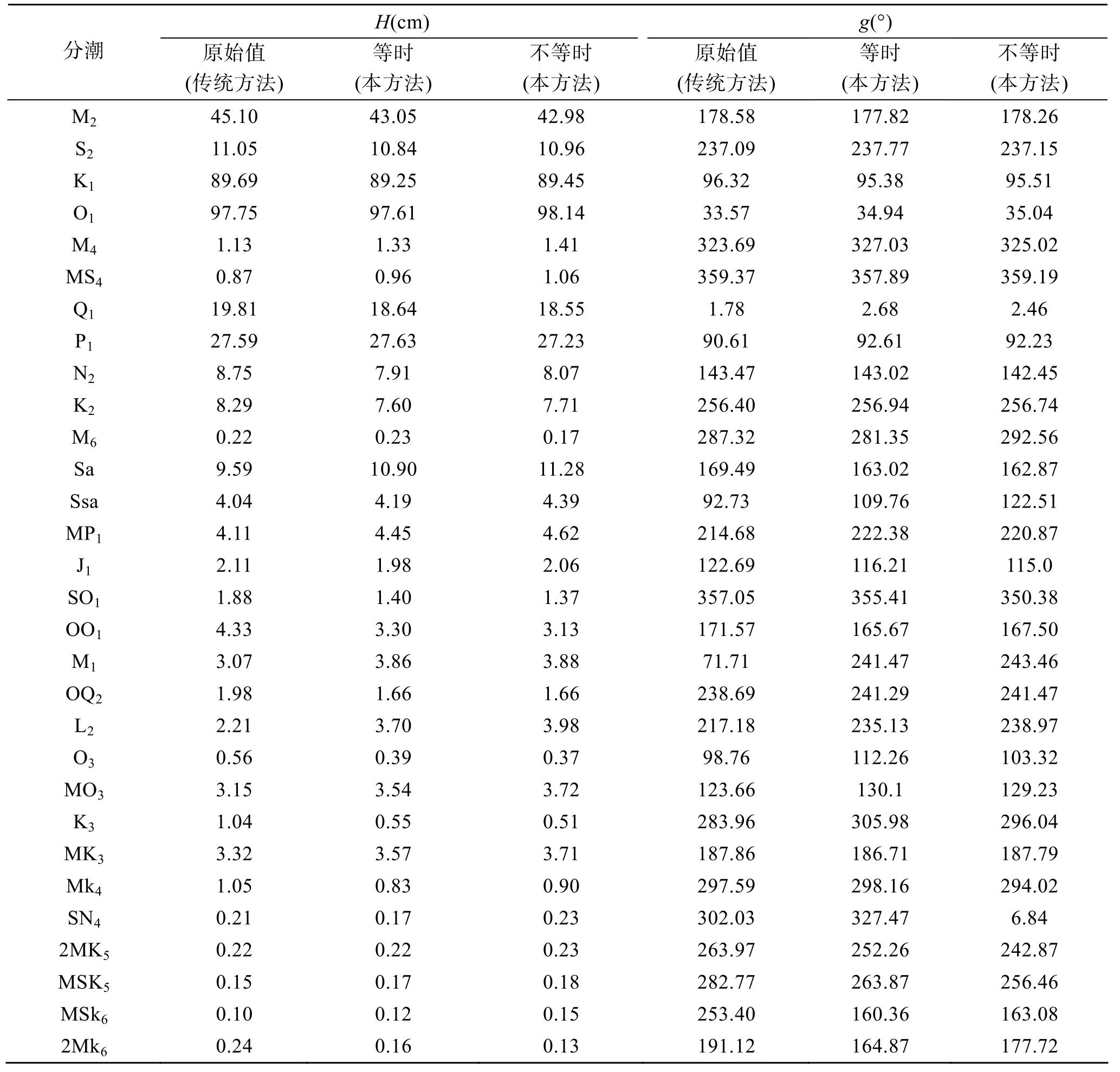
表2 北海原始、等时与不等时资料调和常数比较Tab. 2 The comparison of harmonic analysis of data sampled at equal time intervals and non-equal time intervals in Beihai

在表 3、表 4、表 5、表 6中, 只列出了个别分潮, 本文引入了无单位量纲的负相关系数R, 表示潮汐预报值与原始观测数据的吻合程度[7], 0≤R≤1,其值越大, 代表回归效果越显著, 计算公式如下：

上式中R为负相关系数,U为后报值的离差平方和, 称为回归方差,S为观测资料的总方差,为后报值,为后报值的平均数,yi为观测数据,为观测数据平均数。

从表7中能看出, 当取样间隔为6 h的时候, 变量与原始观测数据的负相关系数为： 大连为 0.9468;北海为 0.9708, 同其余各取样频率结果的负相关系数相比, 相差不是很大。从表4、表6中, 当取样间隔为6 h时, S2分潮迟角一直是60°, 从中分析主要原因为 S2的圆频率为 30°, 为了进一步验证这个假设,当取样间隔为12, 18 h时, 其迟角都是60°/ h, 尤其是其取样间隔为12 h的整数倍时, 此程序无法回报潮位, 也就是说当圆频率与取样间隔的乘积为 180°的整数倍时, 这种基于 Matlab内部函数功能的调和分析方法将是无效的。从表3、表4、表5、表6中不同时间间隔的各分潮的调和常数可以总结出, 随着取样时间的增加, 高频分潮的调和常数误差变大,这就涉及取样间隔与分潮分辨问题, 如果采样间隔∆t取得大, 则采样频率fs(fs=1/∆t)低, 当所分析信号的最高频率fmax大于采样频率fs的二分之一时, 就会引起“频率混淆”现象, 使得原信号中的频率成分出现在数字信号中完全不同的频率处, 造成信号的失真。

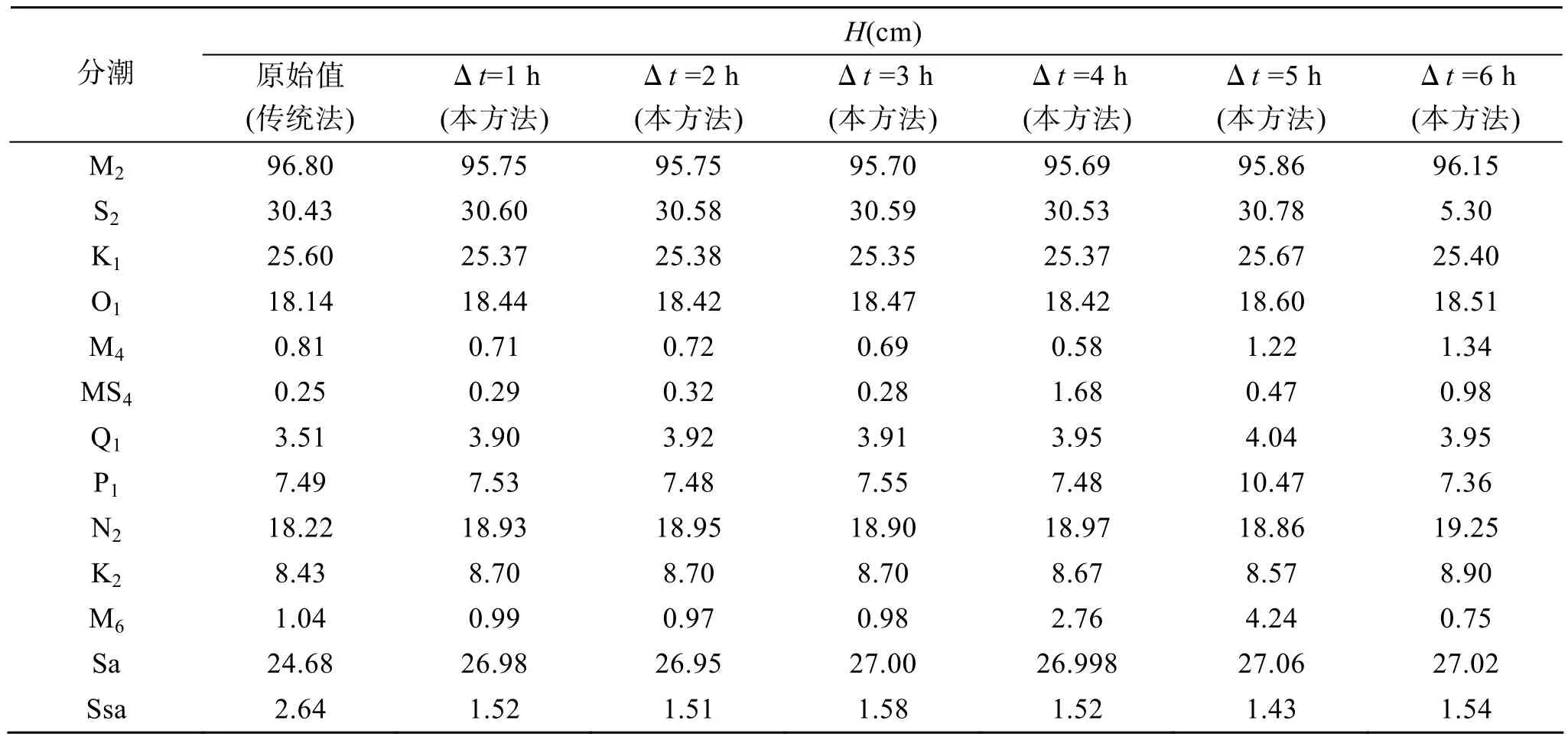
表3 大连原始振幅与各取样间隔不同的观测资料调和分析振幅Tab. 3 The original amplitudes and amplitudes of the harmonic analysis of data sampled at various time intervals in Dalian

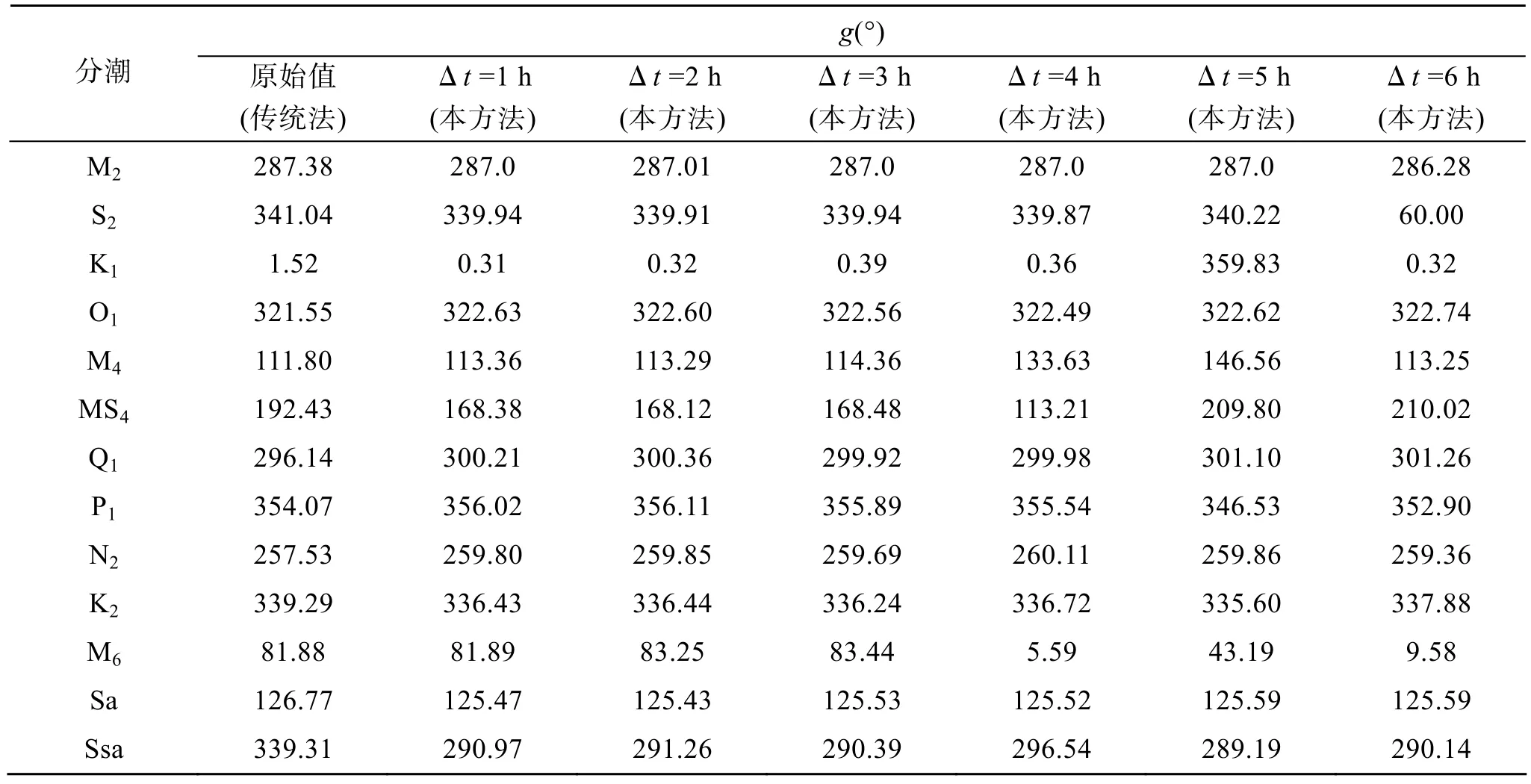
表4 大连原始迟角与各取样间隔不同的观测资料调和分析迟角Tab. 4 The original phases and phases of the harmonic analysis of data sampled at various time intervals in Dalian

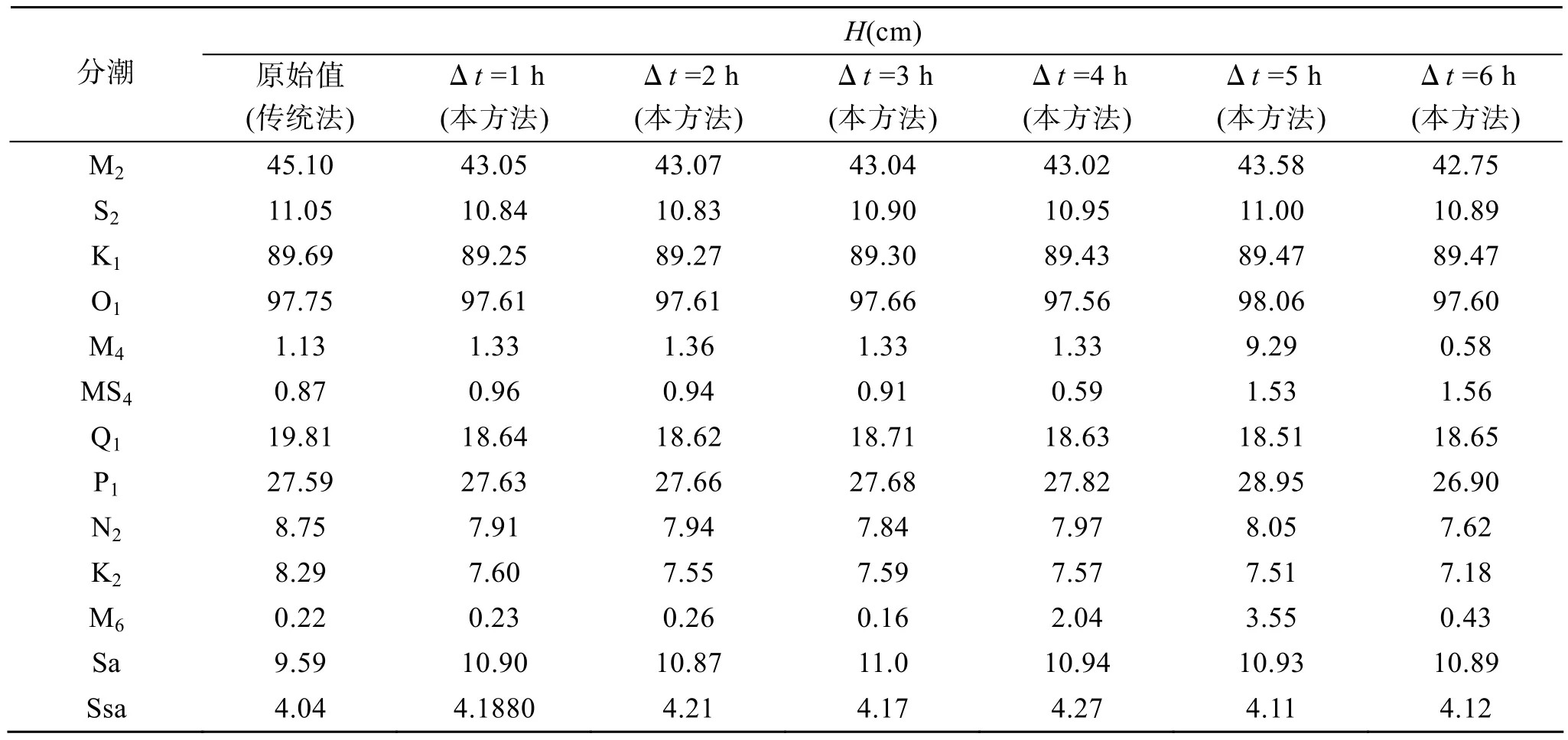
表5 北海原始振幅与各取样间隔不同的观测资料调和分析振幅Tab. 5 The original amplitudes and amplitudes of the harmonic analysis of data sampled at various time intervals in Beihai

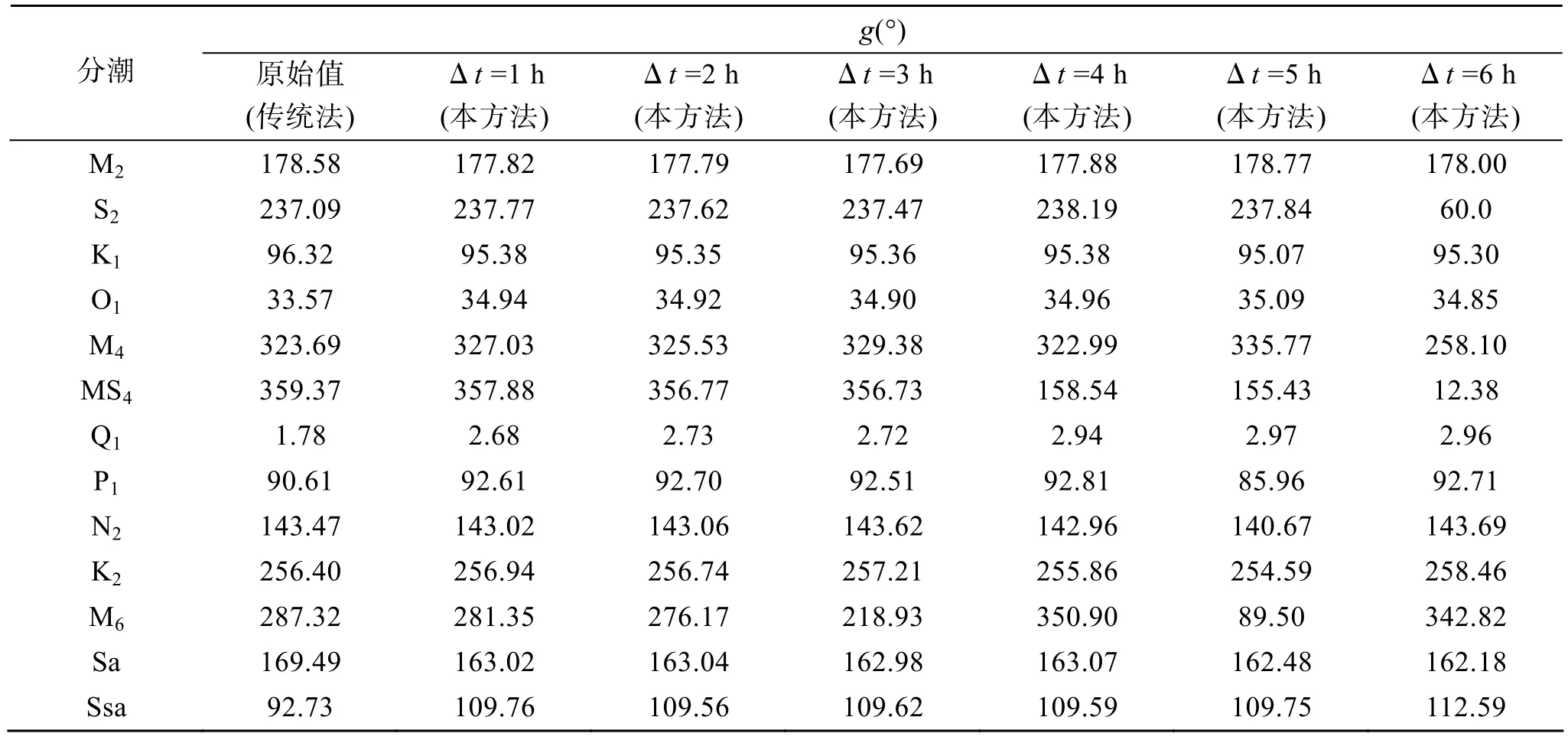
表6 北海原始迟角与各取样间隔不同的观测资料调和分析迟角Tab. 6 The original phases and phases of the harmonic analysis of data sampled at various time intervals in Beihai

表7 大连、北海两站点负相关系数Tab. 7 The negative correlation coefficients in Dalian and Beihai

取样间隔为1 h, 能分辨出圆频率小于180°/s的分潮; 取样间隔为2 h, 能分辨出圆频率小于90°/s的分潮; 取样间隔为3 h, 能分辨出圆频率小于60°/s的分潮。依照σ≤π/∆t公式, 以此类推。

因为取样间隔为1 h和2 h时, 都能分辨出圆频率小于90°/s的分潮, 由于本文用到的30个分潮的圆频率都小于90°/s, 从表 3、表4、表5、表6中可以看到, 当间隔是1 h和2 h时, 分潮的调和常数基本上是一样的, 但随着取样间隔的增大, 像M6, MS4这样的高频分潮就会出现误差, 即发生频率混淆, 高频分潮在调和分析的过程中不能被分辨。

2.2 1个月资料的调和分析

对1个月资料的调和分析, 样品取样间隔为1 h,同样用30个分潮： K1, O1, Q1, P1, MP1, J1, SO1, OO1,M1, M2, S2, N2, K2, OQ2, L2, O3, MO3, K3, MK3, M4,MS4, MK4, SN4, 2MK5, MSK5, M6, MSK6, 2Mk6, Sa,Ssa。选取的月份为 7月份, 选择的站点同样是大连和北海。

应用该方法对潮位进行调和分析时, 结果显示,在大连, Sa的振幅和迟角的值, 以及Ssa的振幅和迟角的值同样不正确, 变量与原始观测数据的负相关系数为0.9911。在北海, Sa的振幅和迟角的值, 以及Ssa的振幅和迟角的值明显不正确, 但是变量与原始观测数据的负相关系数为0.9723。该结果说明, 虽然此种方法应用于潮汐的调和分析时, Ssa, Sa两个分潮的调和常数明显不正确, 但是对于原始潮位资料与后报潮位的拟合, 该方法还是可以实现的。为了说明这个问题, 我们在调和分析的过程中, 去掉 Sa,Ssa两个分潮, 利用其余的 28个分潮对其进行调和分析, 结果发现, 在大连, 变量与原始观测数据的负相关系数为0.9910。在北海, 变量与原始观测数据的负相关系数为0.9926; 从相关系数上判断, 28个分潮与30个分潮调和分析后报值基本上差不多, 甚至30个分潮拟合的结果更加精确(图2)。从Sa, Ssa振幅可以看出, 该方法没有能分辨出这两个分潮, 其主要原因是因为Sa, Ssa是周期约为1 a的长周期分潮, 1个月的资料根本就不能得到他们的调和常数, 也就是说,在调和分析的过程中, 分潮的选取与取样的长度有很大的关系, 最根本的条件就是取样的时间长度必须大于所选分潮的周期。

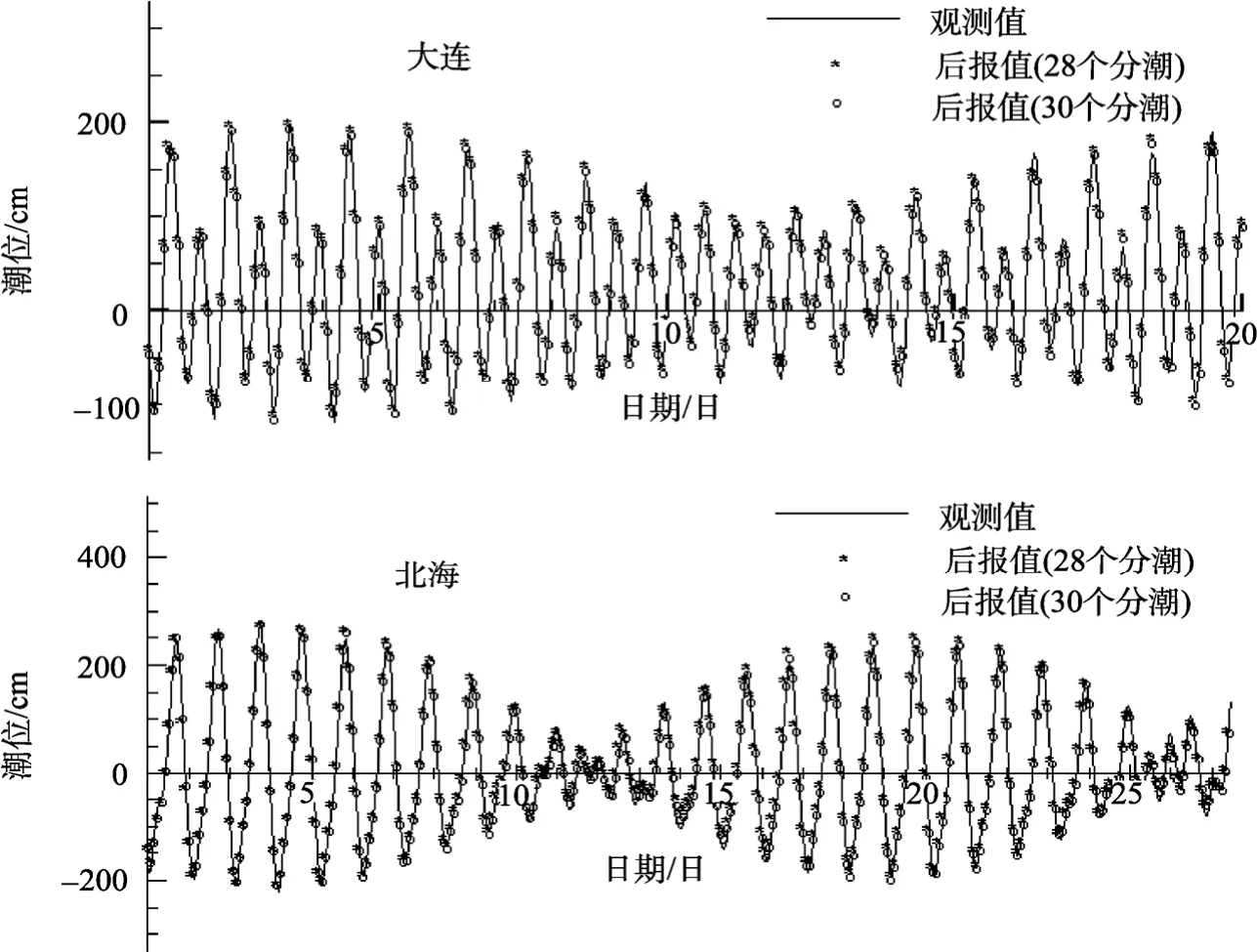
图2 1985年7月大连, 北海1个月潮位观测值、28个分潮和30个分潮调和后报值图Fig. 2 The chart of monthly observation values and hindcast values in Dalian and Beihai in July 1985

3 结论

应用基于Matlab内部函数功能的调和分析方法对已知观测点水位进行调和分析时, 不需要寻找观测资料时间序列的中间时刻来实现对计算的简化,从初始时刻计算即可。其在回报时, 可以采用各个相应时刻的f和u, 使后报结果稍加精确。基于Matlab内部函数功能的调和分析方法与传统调和分析方法相比较, 前者更加简便, 其更显著的优点是此方法可以对任意的观测时间间隔的潮汐水位进行调和分析以及可处理数据漏测或间断情况下的潮汐资料。

通过对大连、北海1985年全年资料的调和分析结果显示, 基于 Matlab内部函数功能的调和分析方法可以应用于等时间序列和非等时间序列的潮汐资料的调和分析, 而且得到的调和常数的精确性比较高, 其预报所得的潮位与实际观测潮位也比较吻合,这说明此种方法完全是可行的。对于不同的取样间隔的观测资料, 随着取样间隔的增加, 对高频的分潮的分辨能力会越来越低, 出现频率混淆的现象。对于 1个月的观测资料的调和分析, 调和分析得到的Ssa, Sa等长周期分潮的调和常数异常, 说明1个月的资料不能分析出周期大于 1个月的分潮, 即观测数据的取样长度必须要大于分潮的1个周期。

本文只是对基于Matlab内部函数的调和分析方法是否可以应用于潮汐调和分析上的一个初步讨论,接下来的工作将是针对不同长度、不同取样间隔的潮汐资料对分潮的选取上做进一步的深入了解, 从而使其调和分析的精度更加精确, 使潮位的回报值更加接近原始资料。

[1]方国洪, 郑文振, 陈宗镛, 等. 潮汐和潮流的分析和预报[M]. 北京：海洋出版,1986： 90-93.

[2]王如龙, 童章龙, 陈耀登, 等. 基于连续函数最小二乘法的潮汐迭代调和分析方法[J]. 中国水利, 2007,7(3)： 116-118.

[3]同济大学应用数学系. 线性代数[M]. 北京： 高等教育出版社, 2004.

[4]David C L. Linear Algebra and Its Applications[M]. 北京： 机械工业出版社,2005.

[5]冯士笮,李凤岐,李少菁, 等. 海洋科学导论[M].北京： 高等教育出版社, 1999： 215-222.

[6]陈宗镛. 潮汐学[[M]. 北京： 科学出版社, 1980：127-144.

[7]施能. 气象科研与预报中的多元分析方法[M]. 北京：气象出版社, 2002. 2： 34-37.

[8]黄祖珂, 黄磊. 潮汐原理与计算[M]. 青岛： 中国海洋大学出版社, 2005： 58-63.

Tidal harmonic analysis

ZHANG Feng-ye1,2, WEI Ze-xun1,2, WANG Xin-yi1,2, WANG Yong-gang1,2, FANG Guo-hong1,2
(1. Key Laboratory of Marine Science and Numerical Modeling, State Oceanic Administration, Qingdao 266061, China, 2. First Institute of Oceanography, State Oceanic Administration, Qingdao 266061, China)

Jan., 24, 2011

Matlab; tide; harmonic analysis; sample

To analyze observational data sampled at non-equal time intervals, we devised a least squares method of tidal harmonic analysis, based on Matlab’s function. By this method, the harmonic constants were almost the same with observational data sampled at either equal time intervals or and non-equal time intervals at Dalian and Beihai in 1985. The harmonic analysis with data sampled at different time intervals showed that frequency aliasing occured when the tidal frequency was more than 1/2 of the sampling frequency, and there were great error when the period of the constituent was significantly larger than the sample length. It was shown that our method could obtain results of the same precision of the traditional method in analyzing discontinuous data or data sampled at non-equal time intervals.

P731.23

A

1000-3096(2011)06-0068-08

2011-01-24;

2011-04-21

国家自然科学基金项目(40976016); 国家海洋局第一海洋研究所基本科研业务费专项资金项目(GY02-2010G07); 国家高技术研究发展计划(863计划)重点项目(2009AA121402)

张凤烨(1985-), 男, 河北唐山人, 硕士研究生, 主要从事物理海洋学研究, E-mail： zhangfy@fio.org.cn; 魏泽勋, 通信作者, 研究员, E-mail： weizx@fio.org.cn

刘珊珊)