用于航空电磁数据调平处理的导数突变点统计法

陈 雄，曾昭发，孙东明，李 静

(1.吉林大学，吉林长春 130026;2.吉林省公路勘测设计院，吉林长春 130026)

用于航空电磁数据调平处理的导数突变点统计法

陈 雄1，曾昭发1，孙东明2，李 静1

(1.吉林大学，吉林长春 130026;2.吉林省公路勘测设计院，吉林长春 130026)

航空电磁数据中经常存在条带状误差，为消除这种误差，通常采用窗口滤波。但是，窗口参数及滤波参数要求极为严格，且不能区分调平误差和其类似大小的地质异常，需要操作者多次尝试以寻求合适的处理参数。这里提出了导数突变点统计法，该方法首先在沿伪切割线方向(垂直飞行方向)，对网格化的航空电磁数据求取伪切割线的导数，采用高通滤波方法滤掉幅值比较小的导数突变点;然后统计每条航线上的突变点个数，根据预设的阈值，确定出存在条带误差的航线;再针对这条航线上的数据，采用均值滤波得到调平结果。导数突变点统计法能自动找出存在误差的航线，并只针对误差线进行滤波，能有效消除条带状误差，极大地保留真实地质异常。导数突变点统计方法算法简单，输入参数少，数据处理速度快，为航空电磁数据调平提供了一种新思路。

航空电磁法;调平;条带状误差;伪切割线法;导数

0 前言

航空电磁法(AEM，AirborneElectromagnetic Method)是基于岩石的电性、磁性等物性差异，应用电磁感应的测量原理，以飞机为测量载体，进行探测的地球物理方法。它是一种快速、高效、经济、适用性强的勘探方法［1～6，9］。航空电磁法数据质量和前期处理方法的好坏，对后期的异常反演、地质解释有着重大的影响［3～5，9］。随着航空电磁法的发展，数据量越来越大，仪器也改进了很多，信噪比得到较大提升。但这些却无法彻底地消除漂移误差，因此室内数据调平，对提高数据质量就显得尤为重要［4、5］。

1991 年，周凤桐［7～10］提出伪切割线调平方法，实现了人机交互调平。1994年，朱月娥［8］提出用条件滤波法消除航磁图像测线干扰条带，这种方法主要是结合中位数法和区间邻点比较法判别异常极值点，能极好地保留有用的地质信息。1999年，FUGRO公司的Huang［1］提出适用于DIGHEM吊舱式直升机频率域电磁系统的二维自动调平法，适用于零漂较小的直升机航电视电阻率数据。2007年，李文杰［9］提出适用于 HDY402三频航电系统的二维移动平均自动调平方法，这种方法不需要网格化处理，方法简单，效率高。2008年 Huang［2］又提出基于线与线之间的航空频率域测量数据的调平方法，取得良好的效果。

上述方法，在很大程度上提高了数据质量。但是这些方法大都采用窗口滤波，而窗口参数和滤波参数很难选择，需要大量尝试才能取得比较好的效果，处理周期长，而窗口滤波很难区分与调平误差相近波长的真实地质信息［9～11］，并且窗口滤波还不可避免地存在边界效应［12］。

基于Huang［1］提出的在块状误差判定时利用导数判定的原理，作者在本文提出基于导数突变点统计法的调平方法，减小了参数选取的难度，算法简单，效率高，并在极大程度上保留了真实地质信息。该方法经实际处理应用，取得了良好的效果。

1 导数突变点统计法的原理

导数突变点统计法计算式为:

其中

其中 i表示网格化后的数据矩阵的某一行，其方向与伪切割线方向相同;j为数据矩阵的列，即沿测线方向;xi，j为原始数据网格化以后的数据矩阵元素;¯xi，j为数据矩阵元素进行一维滤波后得到的结果;N为数据矩阵的行数，即网格化后每条测线上数据点数;M为数据矩阵的列数，即测线总数;PT为高通滤波阈值，即导数值大于PT的点被认为是导数突变点;Nj为第j条测线上导数突变点的统计值;2l+1为一维滤波器长度，其值如何选择将在后面介绍。

根据式(4)，可判断出存在零漂线号:

其中 Lj为一行向量，其值为“1”的元素，所对应的航线即为存在零漂异常的航线;LT为阈值，即只有在每条测线上导数突变点的统计个数大于阈值时，才认为这条线存在零漂。

关于这两个阈值如何选择，作者将在后面介绍。

在确定了含有零漂的测线之后，我们采用均值滤波对其进行处理:其中 x'i，j为调平处理后数据;xi，j为网格化节点数据;¯xi，j为误差线上点一维滤波结果;¯xi，j－1、¯xi，j+1分别为与之相邻测线上的数据点，经过一维滤波后的结果。

此均值滤波器使用方便，实现简单，运算迅速、稳定。

导数突变点统计法是利用统计学方法，来区分出含噪声的测线。只要阈值选取适当，就能准确地找出含噪声的测线。该方法公式简单，但效果明显。

2 导数突变点统计法

在沿伪切割线方向，对每一条伪切割线进行求导时。在导数曲线中存在很多突变点，突变点受系统零漂影响，也受大小不一的地质起伏等因素影响。为了更好地突出系统零漂的影响，压制地质体影响，我们先沿测线方向对数据进行一维滤波(见公式(2))，认为滤波结果为背景值和系统零漂之和，不含地质体影响。然后对一维滤波后的数据沿伪切割线方向进行求导运算，再利用高通滤波公式(1)，滤掉小的由残余地质起伏影响造成的导数突变点。

由于导数值较大的突变点，是由沿测线方向条带误差引起的，所以在高通滤波之后的导数突变点数据上，我们沿测线方向统计每一条测线的导数突变点数量。只要我们选取一个合理的统计点数量阈值，便能得到存在零漂误差的测线(见公式(4))。对每一条误差线进行均值滤波(见公式(5))，最终得到调平结果，具体流程图见下页图1。

在整个处理流程中，两个阈值的选择是该方法能够实现的关键:

(1)如果高通滤波器阈值过小，会引入很多小的导数突变点，给后面的突变点个数统计造成干扰。

(2)如果阈值过大，将遗漏零漂误差线，造成的导数突变点，使滤波不彻底。

统计点个数阈值正确选择的重要意义，与高通滤波器阈值的选择类似。如果两个阈值选择合理，一次滤波便能达到目的。如果发现有含零漂误差的测线遗漏，可进行多次滤波。

阈值选取原则为:

(1)先将原始数据成图，仔细观察误差条带与相邻条带之间的数据差异，以此为高通阈值，或进行微调。

图1 导数突变点统计法处理流程图Fig． 1 Flow chart for the derivative statistics methodleveling procedure

(2)统计阈值一般取值以线上点数的1/3到1/2为宜。

第一步的一维滤波也会对调平质量产生一定的影响:

(1)滤波器长度过长，会产生较强的边界效应，影响数据质量。

(2)滤波器长度过短，不能很好地压制地质体的影响，对导数突变点的求取构成一定的影响。

在一般情况下，一维滤波器的长度选在测线测点数的1/20～1/10之间为宜。

我们把二维移动平均自动调平方法［9、12］与导数突变点统计法做一下对比。二维移动平均自动调平处理过程是在网格化数据的基础上，进行二维均值滤波，滤波结果得到区域背景值。原始网格数据与得到的这个背景值之差，便得到包含调平误差和局部地质异常的中间量。接着再对这个中间量沿测线方向进行一维均值滤波，可以得到调平误差量。原始网格数据减去调平误差量，便得到最终调平结果。

3 数据处理实例

图2为原始航空电磁法频率870Hz实分量异常图。从图2中可以看出，存在很明显的条带状误差，这些误差的存在，掩盖了很多真实的地质信息，如果不加以处理，将会给后面的处理解释带来很大的困难和误差。

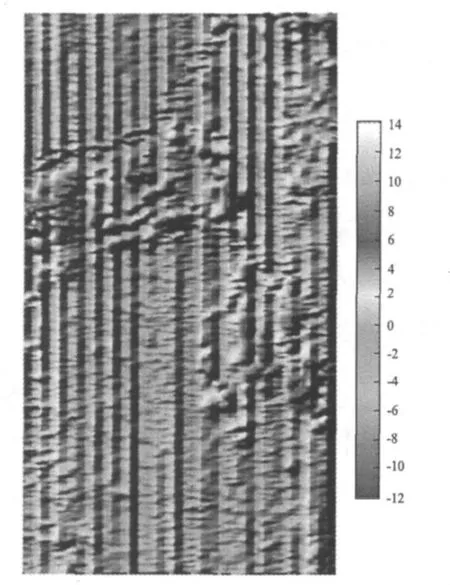
图2 频率为870Hz实分量航空电磁测量原始异常图Fig.2 Raw anomaly map of 870 Hz in-phase component

针对这种情况，我们在这里分别利用导数突变点统计法和二维平均自动调平方法，对其进行了处理，以作对照。在处理过程中，每条航线测点数为9967个，因此一维滤波器长度选为599，高通滤波器阈值我们取值为2.5，统计点个数阈值取3300，即测线上数据点个数的三分之一，M/3。二维移动平均处理二维窗口选为7*399，一维滤波窗口选为999。

经处理后的结果平面图如下页图3所示。其中，图3(a)为二维移动平均自动调平方法处理结果，图3(a)中还包含部份条带误差，图像质量较差。图3(b)为导数突变点统计法处理，带状误差已经被滤掉，并且图像比较光滑，且图3(b)上地质体处数值比二维移动平均方法大，地质信息损耗更少，效果要比二维移动平均自动调平方法处理得好。

图4(见下页)为调平误差，即原始数据与调平结果之间差值。其中，图4(a)为二维移动平均自动调平法调平误差，可以看出，条带误差被滤掉，部份区域有部份地质异常被当作误差滤除了。所以这种方法很难区分与调平误差相近波长的真实地质信息，造成调平过量。而图4(b)为导数突变点统计方法的调平误差，从图4(b)中可以很清楚地看到，滤波只对有误差的测线进行，而无误差的测线则没有被改动，并且无边界效应。由于图4(b)中并没包含明显的地质信息，说明滤波较好地保留了原始地质信息。

图3 航空电磁法频率870实分量调平结果Fig． 3 Leveling result of 870 Hz in-phase component

图4 航电频率870实分量调平误差Fig． 4 Leveling error of 870 Hz in-phase component

在调平后图3中，地质体处数值要比二维平均自动调平方法处理后的值要大一些，更接近实际地质体异常信息。

导数突变点统计法运用简单、高效，但是效果好与坏的关键，在于处理过程中阈值大小的选择。对于处理经验欠缺的操作者，在处理图像之前，应尽量选取几条样线，大致确定阈值范围，以减少尝试周期。

通过利用导数突变点统计法对实际数据进行处理的结果，以及与二维移动平均自动调平法对比后发现，导数突变点统计法参数少，算法简单，运算快捷。调平只针对存在误差的测线，误差更少，更准确，并且不存在边界效应。

4 结论

针对航空电磁测量中存在的条带状测量误差，作者在本文提出了导数突变点统计方法。该方法能根据数据的特点，进行误差消除处理。在方法的实施中，通过沿伪切割线方向(即垂直于飞行方向)求取沿线数据的导数，并统计导数变化较大点的数量，以判断是否包含测量调平误差。在获得含噪声的测线后，采用滤波方法对其进行调平处理。

用本方法与基于窗口滤波的调平方法相比较可知，本方法算法简单，设置参数少，自动化程度高，并能自动识别含误差测线，调平结果更加精确。

通过对本方法和二维移动平均自动调平方法的处理结果对比表明，本方法对于处理存在条带状误差的数据具有较好的效果，并能有效地消除条带误差的影响，完整保留了微小的局部地质体电磁异常。

［1］ HAOPING HUANG，DOUGLAS C． FRASER． Airborneresistivity data leveling［J］． GEOPHYSICS，1999，64( 2) : 378．

［2］ HAOPING HUANG． Airborne geophysical data levelingbased on line to line correlations ［J］． GEOPHYSICS，2008， 73( 3) : 83．

［3］ EIRIK MAURING， OLA KIHLE． Leveling aerogeophysicaldata using a moving differential median filter［J］． GEOPHYSICS，Jan － Feb， 2006， 71( 1) : L5．

［4］ MAJID BEIKI， MEHRDAD BASRANI， LAUST B．Pedersen． Leveling HEM and aeromagnetic data usingdifferential polynomial fitting［J］． GEOPHYSICS，Jan－ Feb，2010， 75( 1) : L13．

［5］ J． BRADLEY NELSON． Leveling total-field aerornagneticdata with measured horizontal gradients［J］． GEOPHYSICS，1994，59( 8) : 1166

［6］ 李文杰.频率域航空电磁数据处理技术研究［D］.北京:中国地质大学，博士学位论文，2008.

［7］ 周凤桐，陈本池，阎永利.航空电磁法数据处理与图示技术［J］.物探与化探，1997(21):348.

［8］ 朱月娥.用条件滤波法消除航磁图像测线干扰条带［J］.物探化探计算技术，1994，16(1):44.

［9］ 李文杰.用于频率域航空电磁数据的二维自动调平［J］.成都理工大学学报，2007，34(4):44.

［10］周凤桐，阎永利，陈本池.航空电磁电阻率填图方法技术及应用研究［R］.河北廊坊:地质矿产部地球物理地球化学勘查研究所，1991.

［11］孙东明，王卫平，曾昭发，等.用于频率域航电数据处理的伪切割线自动调平法［J］.物探与化探，2010，34(2):246.

［12］孙东明，频率域航空电磁法数据处理方法研究［D］.吉林大学，硕士论文，2010.

P631.3+26

A

1001—1749(2011)05—0522—05

2011－01－16 改回日期:2011－06－07

陈雄(1986－)，男，硕士，主要研究方向为工程与环境地球物理勘探，主要从事探地雷达正演模拟及电磁法算法研究。