台风莫拉克、天鹅和艾涛的引导流及相互作用研究*

周 立,李青青,范 轶,端义宏

(1.北京大学物理学院大气科学系,北京100871;2.中国民航云南空管分局,云南昆明650200;3.中国气象局上海台风研究所,中国气象局台风预报技术重点开放实验室,上海200030;4.江苏省丹阳市气象局,江苏丹阳212300;5.国家气象中心,北京100081)

关于影响热带气旋移动的物理机制的研究在过去几十年间取得了许多成果和共识,热带气旋移动的物理过程可以认为是涡旋同环境气流的相互作用过程。作为初级近似,热带气旋可看作是身处大尺度环境流场中的旋转圆柱体,因此其移动与周围环境流关系密切。这种环境流对热带气旋移动的作用称之为“引导(steering)”作用,而相应的流场称为“引导流(steering flow)”。

已有很多研究关注热带气旋引导流的作用[1],如果仅只考虑正压流体情况,涡旋将沿引导流矢量方向移动,但实际上热带气旋的移动时常偏离引导流矢量方向[2],表明除了引导流作用,其他物理过程也影响着热带气旋的移动。例如beta效应的影响,涡旋与地球涡度水平梯度的非线性相互作用,会使得正压涡旋向西北方向移动,造成涡旋移动方向与所受引导流方向出现偏差[3-4]。此外,水平非均匀流会改变环境涡度,导致涡度梯度变化,进而影响台风移动[5]。除了上述正压情况,涡旋和环境大气的斜压作用也会影响台风移动,台风倾向于朝位涡时间变率最大的方向移动[6]。海陆差异也会影响热带气旋的移动,Wong和Chan[7]的数值试验表明,海陆的摩擦差异会导致大尺度流场的非对称性,引导气旋向陆地一侧移动。

尽管上述众多因素影响着热带气旋的移动,但大约超过70%的热带气旋移动主要受环境引导流作用[8]。通常,对流层不同高度的流场结构各不相同,因此如何定义和计算引导流,是研究环境流场对热带气旋引导作用的难点之一。有研究认为对于强度越强的台风,使用深层对流层大气积分所得的引导流与台风实际的移动相接近[9]。此外,确定积分的水平范围也是计算引导流的难点之一,在没有采用涡旋移除技术的情况下,Chan和Gray[10]认为使用离台风中心5(°)～7(°)环状带的切向平均风计算所得的引导流与台风移动矢量相比,两者之间存在最稳定的夹角。但似乎使用不同的资料,针对不同热带气旋个例所得结果各不相同。为更准确地描述环境引导流,计算中去除资料中热带气旋流场信息而保留相应的环境场信息是必要的。本文将通过个例研究,使用涡旋移除技术获得不包含热带气旋信息的环境场,计算相应热带气旋的引导流。

双热带气旋或者多热带气旋相互作用导致的路径变化,通常造成较大的路径预报误差。从引导流角度定性和定量地分析热带气旋间的引导作用,有助于研究多热带气旋相互作用,尤其是对气旋移动的影响。最近Wu等[11]利用位涡反演分析2个热带气旋的相互作用,定量计算了两者相互间的引导作用,而直接利用涡旋分析方法研究多气旋的相互作用以前的研究较少涉及,本文将探讨直接利用涡旋分离技术定量地分析3个发生在西北太平洋热带气旋之间的相互作用的可行性。

1 资料和方法

1.1 资料

文中使用国家气象中心的实时台风定位资料描述台风的位置。美国NCEP的GFS资料用以分析相应的大尺度天气形势和计算台风引导流,其空间分辨率为1(°)×1(°),时间分辨率为6 h。

1.2 引导流的计算

如引言所提,为更准确地计算台风的引导流,可行的1种方法是先移除台风涡旋再计算环境引导流。本文将采用Kurihara等[12-13]和Kwon等[14]提出的涡旋分离技术,相应计算过程简述如下:

(1)选取1个以台风位置为中心的水平经纬网格区域,利用变化平滑系数的3点平滑算子将背景场分离为基本场和扰动场,其中扰动场包括台风涡旋环流和部分大尺度环流扰动。

(2)在以台风中心为圆心的圆柱坐标系中,计算扰动场在24个方位角方向上的近地面切向风和其梯度值,然后根据经验判据(切向风速<6 m·s-1并且切向风梯度<4×10-6s-1,或者切向风速<3 m·s-1)确定台风涡旋环流范围。

(3)在以台风中心为圆心的圆柱坐标系中,确定台风涡旋环流和非涡旋环流部分在24个方位角方向上的边界点,并将这24个边界点的扰动场值作为该点的非涡旋环流值,利用最优插值方法,以初值为0来计算出台风涡旋区域内各点的大尺度形势场值,进而从扰动场中分离出大尺度环流扰动部分。

(4)分离出大尺度环流扰动部分加上基本场,即为去除涡旋环流的环境场,用于计算环境引导流。

计算引导流需要确定计算的垂直层次,本文中计算时最低层为850 hPa,最高层主要通过3种途径确定:散度方法、位涡方法和动力对流层顶方法,各方法简述如下:

(1)散度方法:计算台风区域平均的散度垂直廓线,若区域平均的散度值在连续2个垂直层次为负值,则将第2个垂直层作为计算引导流的最高层。这种方法主要考虑了台风涡旋上层通常为辐散流出层的特征。

(2)位涡方法:计算台风区域平均的位涡垂直廓线,定义最小的平均位涡值所在层次为计算引导流的最高层。

(3)动力对流层顶方法:计算台风区域各点在动力对流层顶(2PVU等位涡面)的气压值的平均值,将最接近此平均值的气压层作为计算引导流的最高层。

然后,在以台风位置为中心7个经纬度范围内,对低层(850 hPa)和最高层之间各层的环境场风速计算密度权重平均,获得引导流。

2 计算结果和分析

本文将采用上述引导流计算方法,分析2009年的3个台风天鹅(Goni)、莫拉克(Morakot)和艾涛(Etau)。这3个台风于2009年8月同时发生在西北太平洋(见图1,2),是比较典型的西北太平洋多台风活动现象。

图1 台风莫拉克(台风标记)、天鹅(空心方块)和艾涛(斜十字)的路径Fig.1 Tracks of Typhoons Mo rakot(typhoon symbols),Goni(hollow squares),and Etau(crosses)

图2 台风天鹅、莫拉克和艾涛2009年8月9日00··00 FY2C卫星红外云图Fig.2 IR satellite imagery derived from the FY2C of Typhoons Goni,Morakot,and Etau at 00 UTC 9 August,2009

2.1 2009年台风天鹅、莫拉克和艾涛

台风天鹅于2009年8月3日12··00(世界时,下同)生成于南海北部洋面,随后受副热带高压影响(见图2),其向西北方向移动(见图1),强度缓慢增强(见图3)。天鹅于8月5日20··00左右在广东省中部沿岸登陆,登陆时最低中心气压约为995 hPa(见图3)。登陆后,由于同莫拉克有相互作用,天鹅折向西南方向移动,强度减弱为热带低压(见图2)。8月7日03··00左右天鹅进入北部湾洋面(见图1),强度再次增强为热带风暴(见图3)。随后,天鹅沿着海南岛逆时针移动,于8月9日08··00在海南岛以东250 km附近消亡。

图3 台风莫拉克、天鹅和艾涛的最低中心气压(hPa)随时间的变化Fig.3 Time series of theminimum central p ressure(hPa)of Typhoons Morakot,Goni,and Etau

台风莫拉克由季风槽中活跃的对流系统发展而来。生成后其受副热带高压偏南气流引导(见图4ac),向偏西方向移动(见图1),强度快速增强,在8月6日00··00达到最大强度(最低中心气压为960 hPa),随后强度维持了48 h(见图3)。在台湾岛登陆后,莫拉克的强度逐渐减弱,受南侧偏南气流影响(见图4df),路径向北折,最后于8月11日08··00消亡(见图1)。

台风艾涛同样由季风槽中的低压系统发展而来。其生成后受副热带高压偏南气流的影响向北移动(见图1),强度缓慢增强,最低中心气压减小至990 hPa(见图3)。随后,受中纬度西风槽系统影响,移动路径向东偏折,强度减弱,最后于8月12日08··00消亡(见图1)。

图4 2009年8月(a)4日00··00,(b)5日00··00,(c)6日00··00,(d)7日00··00,(e)8日00··00和(f)9日00··00的动力对流层顶风场和位温分布Fig.4 Winds(barbs)and potential temperature(shading;unit:K)on the dynamical tropopause at(a)00 U TC 4,(b)00 UTC 5,(c)00 U TC 6,(d)00 U TC 7,(e)00 UTC 8,and(f)00 U TC 9 August,2009

2.2 台风环流的移除

以8月7日12时台风莫拉克为例,图5a为莫拉克850 hPa风场,相比其东侧的低压系统(后发展为台风艾涛)和西侧的台风天鹅环流系统,莫拉克的环流系统尺度明显较大,其南侧与强盛的西南季风环流相连。采用2.2中所述的涡旋分离方法获得的莫拉克850 hPa风场如图5b所示,台风中心附近气旋式环流被分离出来,较大的环流风场位于莫拉克中心附近,整个环流场并呈现出非对称特征。值得注意的是采用上述方法莫拉克中心西侧和西南侧超过1 000 km的较远区域也包含了涡旋流场信息,这表明采用上述涡旋分离技术时,季风和其他热带气旋等复杂系统可能会影响台风涡旋环流的计算,但分离得到的这部分区域的风速较台风中心附近环流风速要小得多(见图5b)。图5c为移除莫拉克台风环流后所得的环境流场,可见与图5a相比,莫拉克中心附近的较大的涡旋流场被移除,基于此环境流场计算相应时刻的引导流。

图5 2009年8月7日12··00台风莫拉克850 hPa高度的全风场(a),涡旋风场(b)和环境风场(c)Fig.5 (a)850 hPa full w inds,(b)w inds associated with the vortex,and(c)environmental w inds of Typhoon Mo rakot at 12 U TC 7 August,2009

采用前述涡旋分离方法,同样能够非对称地移除台风天鹅和艾涛的涡旋环流(图略)。

2.3 2009年台风天鹅、莫拉克和艾涛的引导流

图5是台风莫拉克、天鹅和艾涛的引导流和台风移动矢量。

对于台风莫拉克,大多数时刻3种确定垂直平均高度方法所得到的引导流矢量方向大致接近实际台风移动方向(见图6),散度、动力对流层顶和位涡方法确定垂直平均高度计算所得的引导流矢量方向同台风移动方向的平均夹角(平均夹角偏差)非常近似,分别为-78.3(°)(56.5(°))、-79.6(°)(55.7(°))和-80.4(°)(53.8(°))①平均夹角指引导流矢量同台风移动矢量的方向差的平均值;平均夹角偏差指夹角绝对值的平均值。夹角正(负)值表示矢量方向指向参考矢量方向左(右)侧,下同。,即平均而言,计算的引导流方向都指向莫拉克移动方向右侧,这与Chan和Gray的结果一致。散度、动力对流层顶和位涡方法确定垂直平均高度计算所得的平均的引导流大小与台风移速之差的分别为-1.1、-0.94和-1.0 m·s-1,表明平均而言台风莫拉克的引导流小于台风的移速,但是值得注意的是计算的引导流大小与移速的平均偏差分别为2.4、2.6和2.3 m·s-1。具体分析莫拉克生命期不同时段的引导流发现,从莫拉克生成至增强为强热带风暴,引导流方向主要指向台风移动方向右侧(见图6);随后引导流方向同莫拉克移动方向基本一致,但8月6日00··00后,引导流方向和台风移向的偏差明显增大,例如7日06··00引导流方向接近与莫拉克移向相反,这可能与本文使用实时业务台风中心定位资料有关,此台风中心定位资料还未经过最终的订正,因此在有复杂地形(如台湾岛)影响时,可能会出现中心定位的不确定,导致计算的台风移动不准确。8月7日18··00后,引导流方向转变为偏东北,莫拉克也随之向偏北方向移动,且8月7日18··00～9日06··00,引导流大小均大于相应时刻莫拉克移速(见图6)。另外,对于台风莫拉克,只有少数时刻3种确定垂直平均高度方法所得到的引导流矢量之间差异较明显,例如8月6日1200(见图6),此时使用散度方法、动力对流层顶方法和位涡方法确定的求垂直平均时的最高层次分别为500、400和200 hPa。

对于台风天鹅,散度、动力对流层顶和位涡方法确定垂直平均高度计算所得的引导流矢量方向同台风移动方向的平均夹角(平均夹角偏差)也较近似,分别为-143.9(°)(58.6(°))、-154.4(°)(60.0(°))和-148.4(°)(60.8(°)),平均而言天鹅的引导流方向也指向涡旋移动方向的右侧,但当天鹅向西南方向移动时(8月6日06··00～8日00··00),其环境引导流方向常指向涡旋移动方向左侧(见图6)。散度、动力对流层顶和位涡方法确定垂直平均高度计算所得的引导流大小与台风移速差的平均值远小于莫拉克,分别为0.06、0.21和-0.06 m·s-1,而计算的引导流大小与移速的平均偏差相则较大,分别为1.4、1.8和1.2 m·s-1。天鹅的环境引导流矢量最显著的特征是8月5日12··00～9日00··00期间气旋式的旋转,对应天鹅路径气旋式打转现象(见图6),表明台风莫拉克和天鹅相互靠近过程中发生相互作用,这将在下一小节讨论。

台风艾涛在8月9日12··00才生成,但作者跟踪其生成前的低压系统(将1 000 hPa上的位势高度低值中心作为低压中心),并计算相应的环境引导流。对于艾涛,使用散度、动力对流层顶和位涡方法确定垂直平均高度计算所得的引导流矢量方向同台风移动方向的平均夹角有明显差别,分别为-41.0(°)、-27.3(°)和-53.3(°),而平均夹角偏差则相近,分别为43.2(°)、40.5(°)和37.3(°)。散度、动力对流层顶和位涡方法确定垂直平均高度计算所得的引导流大小与台风移速之差的平均值分别为-0.74、-0.46和-0.80 m·s-1,同样表明平均的台风艾涛的引导流小于其移速,而计算的引导流大小与移速的平均偏差分别为3.3、3.5和3.6 m·s-1。8月7日00··00至9日18··00期间,艾涛的环境引导流大多指向东北偏北方向,对应着艾涛偏北方向的移动;其后,环境引导流转向东北向,艾涛的路径也随之向东北方向转折(见图6)。从图6还可以看出,与莫拉克和天鹅相比,平均而言艾涛的环境引导流相对较大。

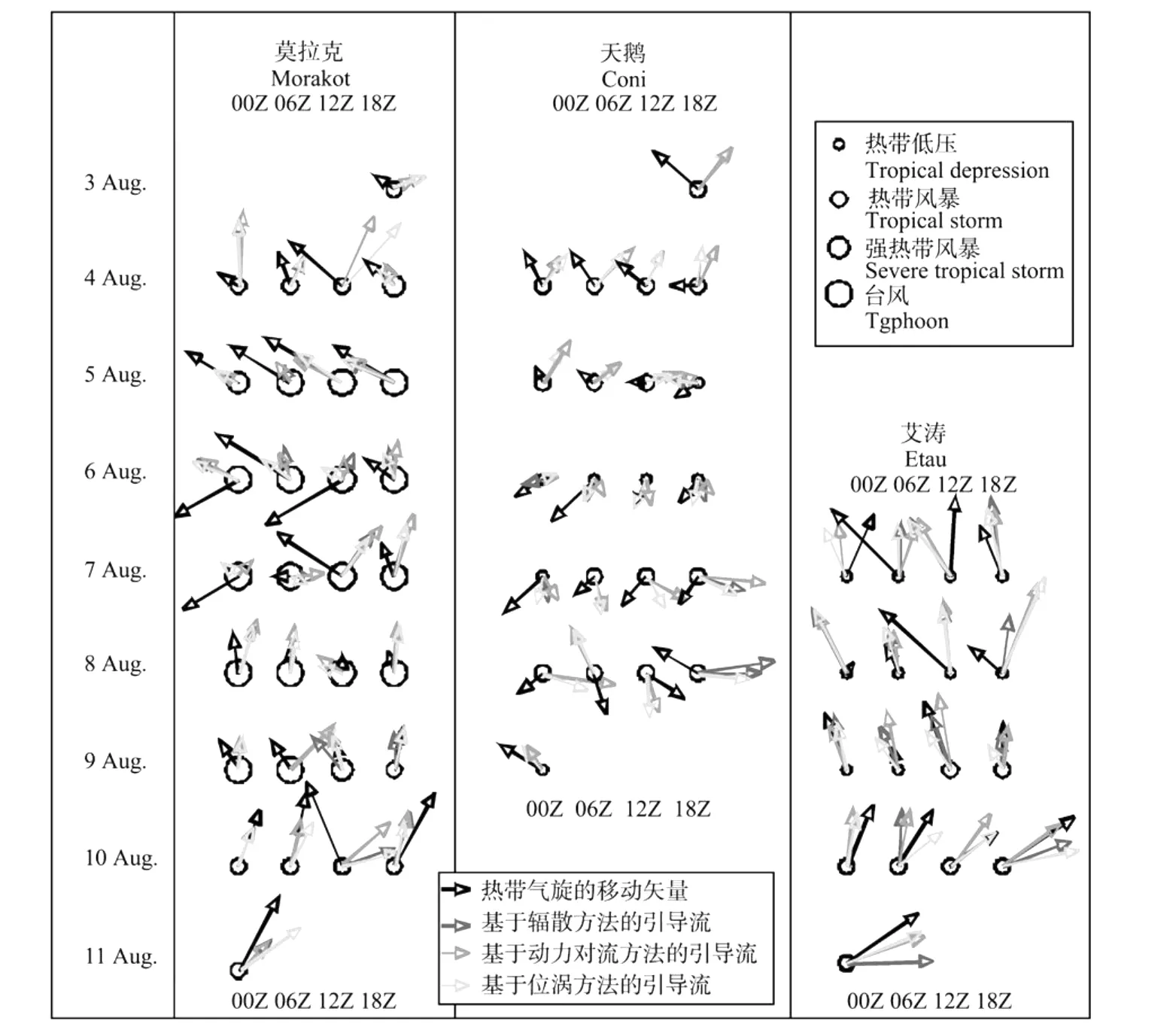
图6 台风莫拉克、天鹅和艾涛的移动矢量和引导流矢量Fig.6 Movement and steering-flow vectors of Typhoons Morakot,Goni,and Etau

2.4 2009年台风天鹅、莫拉克和艾涛的相互作用

由于莫拉克、天鹅和艾涛一段时期内同时活跃在西北太平洋,可能出现相互作用,这一小节将讨论这些相互作用,主要关注对路径的影响,分析的时段为8月7日00··00～9日00··00。

利用2.2节介绍的涡旋分离方法,若要计算某一时刻台风莫拉克的存在对天鹅和艾涛所受引导流的作用,可以在FNL资料中先将莫拉克的涡旋环流移除,再计算此时剩下2个天鹅和艾涛各自的环境引导流,将这些引导流同没有移除莫拉克时计算所得引导流进行比较,以此方法获得此时莫拉克对天鹅和艾涛环境引导流的作用。以此类推,可以分别计算天鹅或者艾涛对其他两台风环境引导流的作用。相应的结果见图7。

从图7可知,3种确定垂直平均高度方法计算所得的台风间的相互作用并没有十分显著的差异。从8月7日00··00～8日06··00,台风天鹅和艾涛都对莫拉克有东北向的引导作用,主要是与天鹅和艾涛南侧的西南气流有关(见图5c),其中前2个时刻的引导作用弱于后面时刻(见图7)。值得注意的是从7日12··00～8日06··00,尽管天鹅和艾涛都对莫拉克有相对较强的东北引导作用,但莫拉克所受环境引导流大小仅只和天鹅或者艾涛对其的引导作用相当,这是由于莫拉克西侧大陆高压对莫拉克有着偏南的引导作用(见图4e)。8月8日12··00,天鹅和艾涛对莫拉克的引导作用同时减弱并调整为西南向。8日18··00和9日00··00,鹅和艾涛对莫拉克的引导再次转变为东北方向(见图7)。

从上文分析发现,台风天鹅的环境引导流方向随时间呈气旋式变化(见图6,7),从图7可知这主要是由于台风莫拉克和天鹅的相互作用有关,莫拉克对天鹅的引导作用随时间明显表现出气旋式旋转。Lander和Holland[15]认为双热带气旋相互作用的过程起初为相互靠近,通常是反气旋式地靠近,然后经历相互捕捉过程,接着发生长时间互旋,互旋过程中两气旋可能相互接近,也可能彼此分离。而莫拉克和天鹅的相互作用过程中,并没有出现明显的互旋现象,仅只表现在天鹅路径有气旋式旋转(见图1)。这可能是由于莫拉克环流系统的水平尺度和涡旋强度都比天鹅大得多(见图5),在相互作用过程中莫拉克起着主导作用。由于中心相距较远,艾涛对天鹅的引导作用相对较弱(见图7)。

莫拉克环流对艾涛的引导作用主要为偏北方向,与艾涛所受环境引导流的方向基本一致,而天鹅对艾涛的引导作用相对较弱(见图7)。

3 结语

本文通过2009年台风莫拉克、天鹅和艾涛的3个个例研究,分析了使用涡旋分离方法移除涡旋环流并计算台风环境引导流的可行性。利用涡旋分离技术,可以将FNL资料中的台风涡旋环流非对称地移除,克服了以前计算台风环境引导流时未去除台风环流信息或者仅只对称地移除台风环流的缺点。计算引导流时,确定垂直平均的高度也是难点之一,本文中采用散度、动力对流层顶和位涡3种方法确定垂直平均的最高层次。通过分析发现,此方法可以有效地获得台风相关引导流信息。通过涡旋移除技术,还进一步分析了莫拉克、天鹅和艾涛之间的相互作用,发现在8月7日00··00～9日00··00期间,天鹅和艾涛主要对莫拉克有向北的引导作用,天鹅的路径气旋式旋转主要是由于莫拉克环流的作用,莫拉克环流对艾涛有着向北的引导作用,而天鹅和艾涛之间的相互作用相对较小。计算引导流时,3种方法确定垂直平均的最高层次所获得的结果差异不大。

由于资料和算法等原因,本文中使用的计算引导流的方法可能存在以下缺点。本文中使用FNL资料由于其较低的水平分辨率,不能准确提供台风涡旋环流信息,尤其当实际台风强度较强时,通常FNL资料中相应涡旋的强度较观测弱,这可能使得移除的涡旋环流,尤其是台风中心附近环流和实际台风环流有偏差。台风的中心定位和FNL资料中相应涡旋的中心可能存在偏差,这使得移除涡旋环流时产生误差。另一方面,当台风环流同其他系统相互作用时,例如与强盛西南季风或者中纬度槽系统相互作用时,文中使用的涡旋分离技术,可能不能够准确地分离台风环流,从而影响环境引导流计算的精确程度。

作为系列研究的第一步,本文仅只以3个台风为例,分析了涡旋分离技术在计算环境引导流中的可行性和相应的引导流特点。要进一步研究此方法对确定台风环境引导流的实用性和相应引导流特征,例如,三中确定垂直平均高度方法的优劣和实用性,引导流的大小和方向同台风实际移动的方向和移速的关系等,需要进行大量样本的分析,并调查统计特征,这将在后续文章中阐述。

[1] Elsberry R L.A global view of tropical cyclones[M].Chicago:Univ Chicago Press,1987:185.

[2] Carr L E III,Elsberry R L.Observational evidence for prediction of tropical cyclone propagation relative to environmental steering[J].J Atmos Sci,1990,47(2):542-546.

[3] Chan JC L,Williams R T.Analytical and numerical studies of the beta-effect in tropical cyclone motion.Part I:zero mean flow[J].J Atmos Sci,1987,44(9):1257-1265.

[4] Fiorino M,Elsberry R L.Some aspects of vortex structure related to tropical cyclone motion[J].J Atmos Sci,1989,46(4):975-990.

[5] Williams R T,Chan JC L.Numerical and analytical studies of the beta-effect in tropical cyclone motion.Part II:Zonal mean flow s[J].J Atmos Sci,1994,51(5):1065-1076.

[6] Wu L G,Wang B.A potential vorticity tendency diagnostic approach for tropical cyclone motion[J].Mon Wea Rev,2000,128(6):1899-1911.

[7] Wong M L M,Chan JC L.Tropical cyclone motion in response to land surface friction[J].J Atmos Sci,2006,63(4):1324-1337.

[8] Neumann CJ.The joint typhoon warning center(JTWC92)model[R].[s.l.]:SA IC,Final Report,Contract No.N00014-90-C-6042,1992:85.

[9] Velden C S,Leslie L M.The basic relationship between tropical cyclone intensity and the depth of the environmental steering layer in the Australian region[J].Wea Forecasting,1991,6(6):244-253.

[10] Chan J C L,Gray W M.Tropical cyclone movement and surrounding flow relationships[J].Mon Wea Rev,1982,110(10):1354-1374.

[11] Wu CC,Huang T S,Huang W P,et al.A new look at the binary interaction:Potential vorticity diagnosis of the unusual southward movement of Tropical Storm Bopha(2000)and its interaction with Supertyphoon Saomai(2000)[J].Mon Wea Rev,2003,131(7):1289-1300.

[12] Kurihara Y,Bender M A,Ross R J.An initialization scheme of hurricane models by vortex specification[J].Mon Wea Rev,1993,121(7):2030-2045.

[13] Kurihara Y,Bender M A,Tuleya R E.Improvements in the GFDL hurricane prediction system[J].Mon Wea Rev,1995,123(9):2791-2810.

[14] Kwon H J,Won S H,Ahn M H.GFDL-type typhoon initialization in MM 5[J].Mon Wea Rev,2002,130(12):2966-2974.

[15] Lander M,Holland G J.On the interaction of tropical-cyclonescale vortices.I:Observations[J].Quart J Roy Meteor Soc,1993,119(10):1347-1361.