人工回灌控制基坑工程地面沉降的数值模拟*

瞿成松,陈 蔚,黄 雨

(1.北京师范大学水科学研究院,北京100875;2.地下水污染控制与修复教育部工程研究中心,北京100875;3.上海长凯岩土工程有限公司,上海200002;4.同济大学,上海200092)

1980年代以来,基坑降水技术在国内蓬勃开展起来,目前基坑降水控制中心由降水水位转移到以降水引起的土体变形,地下水回灌显得特别重要,而基坑降水中地下水回灌模型和应用较少,本文以上海地铁2、4、9号3条地铁线所围基坑降水为例,基于现场“降水-回灌”过程中水位的实测资料,分析地下水水位、回灌时间、回灌量与沉降量之间的关系,简述下负荷面剑桥模型在地下水回灌工程中的应用。

1 下负荷面剑桥模型

A saoka于2002年在剑桥模型基础上建立了下负荷面剑桥模型并进行了验证[1],Hashiguch及Ueno[2-3]提出下负荷面的概念以解决屈服面内应力状态无法造成塑性应变的问题,它有如下2个基本特征:(1)连续平滑的弹塑性应力应变关系;(2)下负荷面是经过当前应力点并和正常屈服面几何相似的面。后来,张锋借用Nakai于2004年提出的土的密度的概念[4],在传统剑桥模型的基础上,加入了1个反映土体超固结比的状态变量,结合下负荷面的概念,推导了1个超固结重塑粘土的下负荷面剑桥模型[5]。

下负荷面剑桥模型是基于下负荷面概念在剑桥模型基础上推导出来的,能够合理描述黏土卸载再加载的特性,从而反映超固结黏土的应力应变特性,弥补了传统本构模型的不足,是一个很有应用价值和发展前途的岩土本构模型[6]。物理方程中基于下负荷面剑桥理论,联合平衡方程、协调方程和渗流方程,可建立水-土耦合的地面沉降数学模型。

依据下负荷面的物理意义,下负荷面剑桥模型的屈服面方程(亦即下负荷面方程),流动法则(采用联合流动法则)及协调方程如下[7]:

2 工程应用

2.1 基坑降水回灌实施

上海盛大基坑西北侧福山路下有地铁4号线区间隧道;基坑北侧世纪大道路下有地铁2号线区间隧道。地铁2、4号线均处于运营阶段。地铁2号线与基坑北侧之间将有9号线盾构准备穿越(见图1)。2007年10月4日开始基坑开挖,设置5道水平支撑,大底板开挖深度20.75 m,主楼深坑开挖深度27.05 m。降水平面布置如图2,坑内设置42口降水井Y1-Y42及5口观测井J1-J4、J12,坑外设置观测井G1-G6,和7口回灌井H1-H7,回灌井布置在福山路和世纪大道侧(见图3)。

图1 基坑与地铁区间隧道关系位置剖面图Fig.1 Profiles of the metro tunnels and foundation pit location

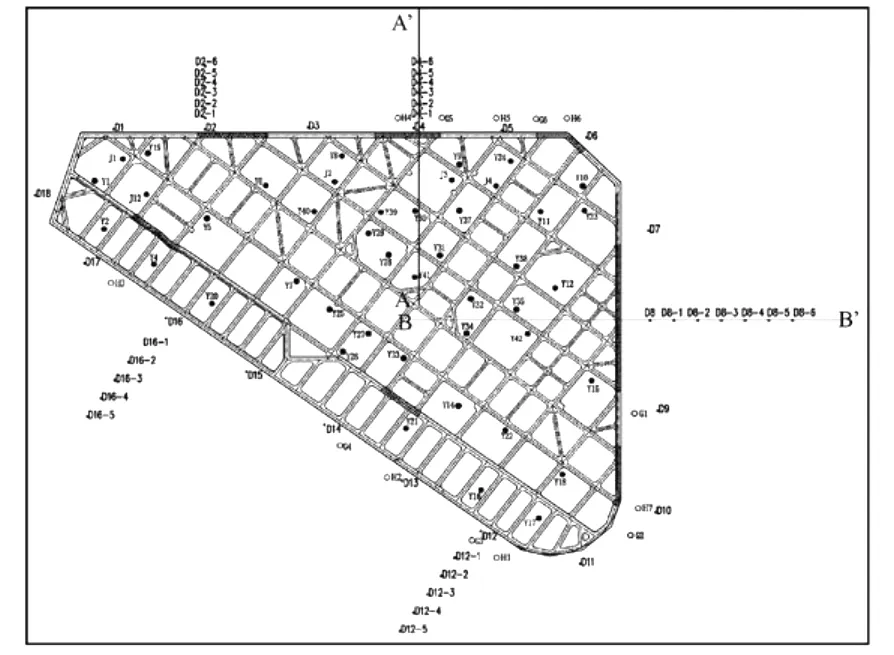
图2 降水井、监测点及计算剖面位置图Fig.2 Profile of dewatering well,subsidence point and calculated

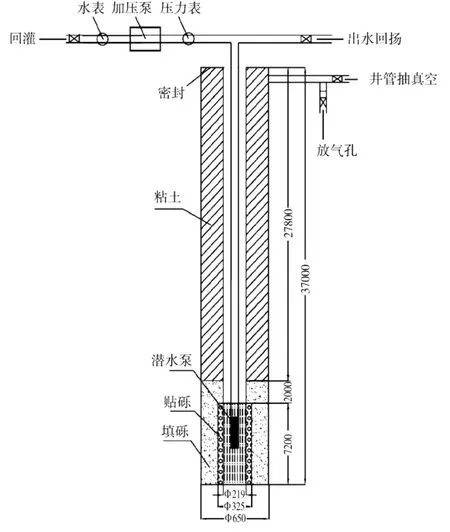
图3 回灌井剖面结构示意图Fig.3 Sketch of recharge well profile

2.2 回灌中基坑开挖深度、地面沉降及水位控制分析

降压降水从第5层土方开挖开始(见图4,5和6)。2007年11月23日～2008年9月29日开启降压井降水,确保了基坑顺利开挖和封底。观测点与回灌井H1～H7布置(见图2)。坑外回灌于2007年12月12日开始～2008年2月25日结束。

基坑施工过程中监测了基坑开挖期间坑外土体地面沉降,图7～10所示各监测点地面沉降变化曲线图。坑外回灌于2007年12月12日开始,此时大底板开挖进行中。大部分监测点的地面沉降于回灌当天开始恢复,回灌初期恢复值较大,为1～2.5 mm,随后继续沉降但沉降速率较未回灌时明显变缓。由监测点监测的地面沉降数据得知在基坑底板养护期间地面高度基本保持不变,说明坑外地面沉降主要由基坑开挖导致,而坑外人工回灌在一定程度上抑制了地面沉降。

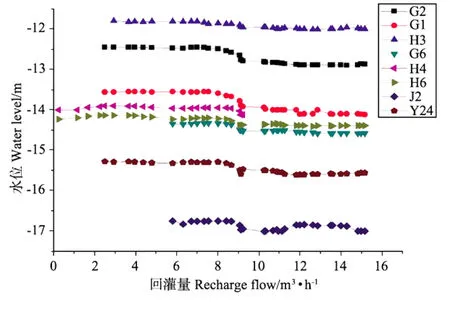
图4 观测井水位随回灌量变化图Fig.4 Sketch of waterlevel-recharge flow curve

图5 地下水水位和开挖深度历时变化图Fig.5 Sketch of waterlevel and depth of excavation-time curve

2.3 基坑施工过程中地面沉降的数值模拟

2.3.1 物理模型概化及计算参数 根据土层分布确定计算模型,由勘察和经验值给定各土层本构参数,设定计算模型边界条件,作网格离散,设定初始应力场,开始计算,然后结果后处理。本次模拟采取以下基本假设:本问题为平面应变问题。井点降水前,土体自重固结已完成。埋设井点引起的土体应力变形暂不考虑。

11月上旬的国内尿素行情维持波动趋势亦属预料之中，出乎意料的却是主产区报价再度反扑至2100-2150元/吨，虽然此番抄底采购的主流成交价控制在2050-2080元/吨，但尿素工厂动辄2150元/吨的虚报态度显然是在为下一轮降价预留“博弈空间”。据了解，上周初的主力需求来自所谓的某大贸易商，而知情人却道出其为拉低前期2100元/吨采购成本的内情，而这万吨以上2030元/吨的成交量也算给本应跌破2000元/吨出厂价的尿素行情打了一剂“强心针”，至于效果能维持多久，想必本周市场的低迷成交与观望氛围已不言自明。

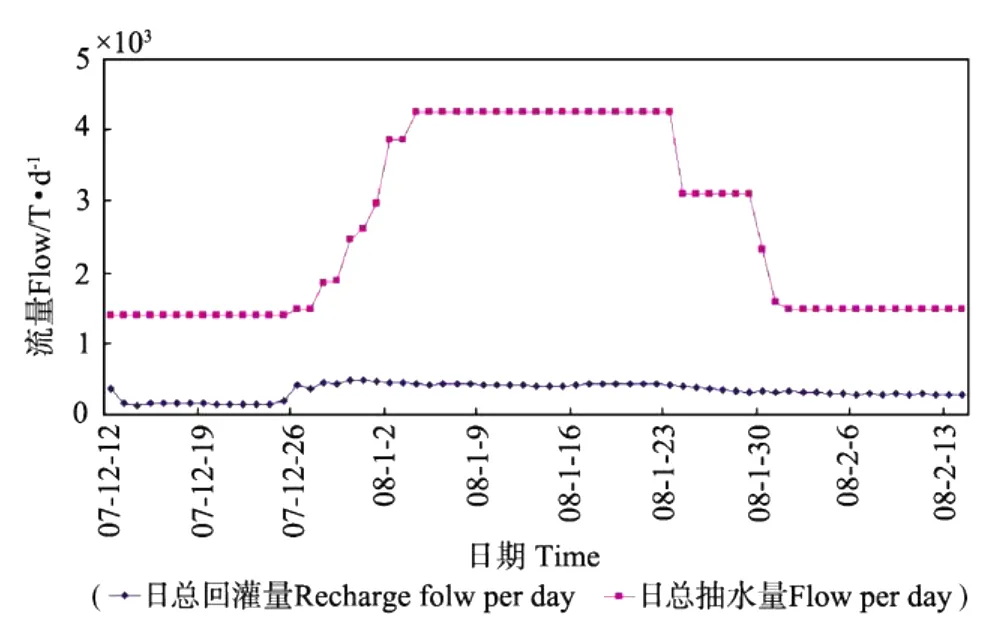
图6 日抽水量和回灌量历时图Fig.6 Sketch of flow-time curve of dewatering and recharge

图7 监测点D2剖面地面沉降历时图Fig.7 Sketch of subsidence-time curve of D2 profile

图8 监测点D4剖面地面沉降历时图Fig.8 Sketch of subsidence-time curve of D4 p rofile

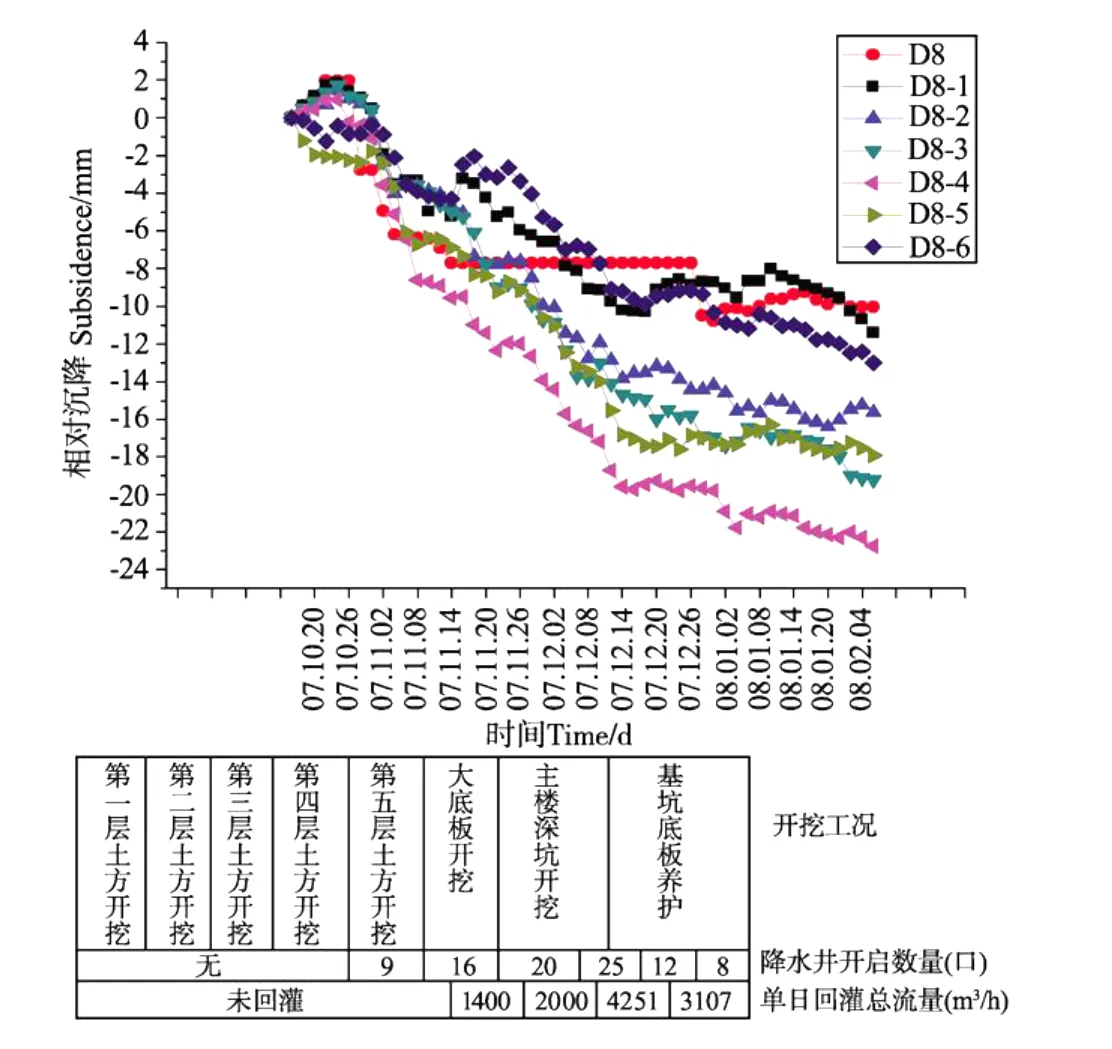
图9 监测点D8剖面地面沉降历时图Fig.9 Sketch of subsidence-time curve of D8 profile

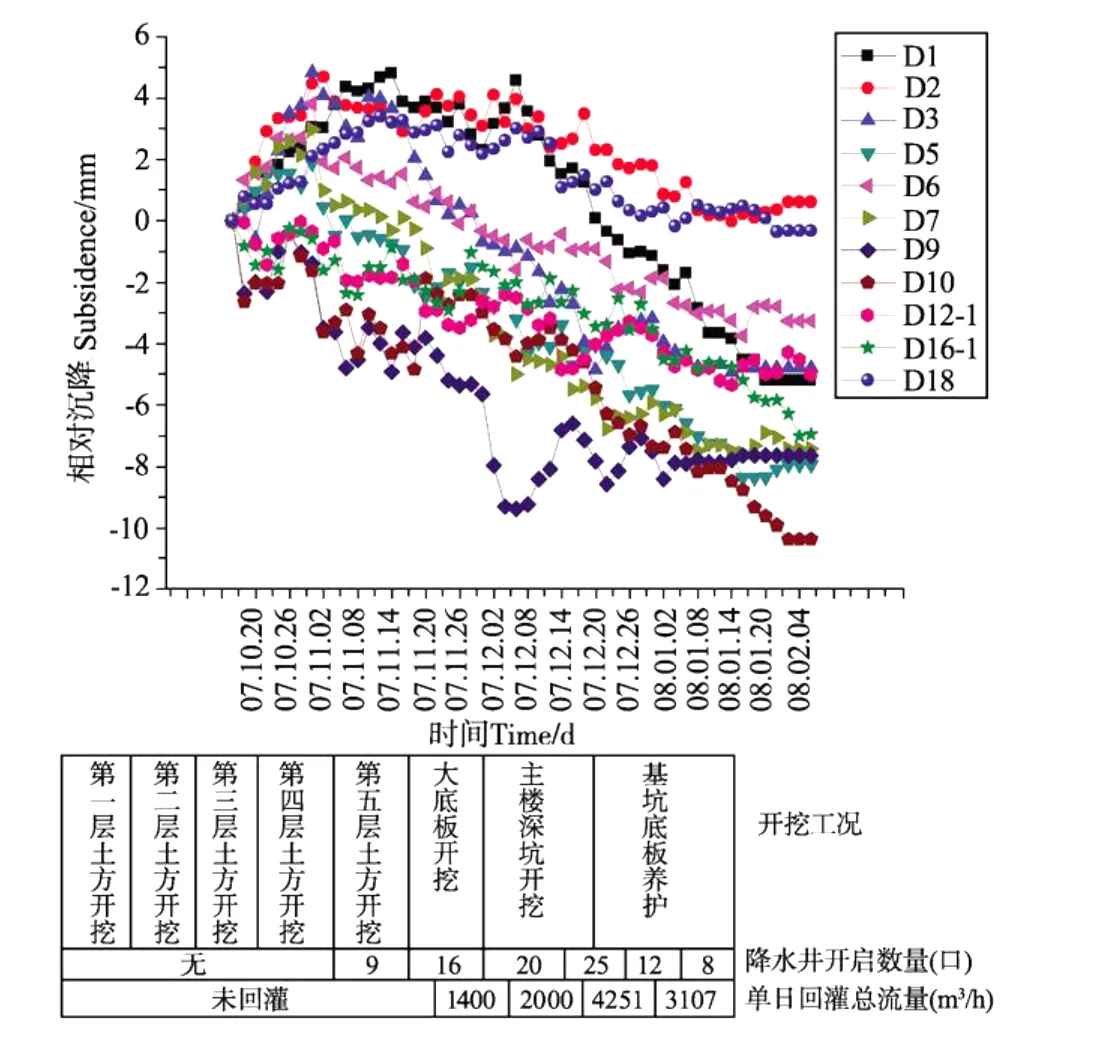
图10 基坑周边监测点D1～18地面沉降历时图Fig.10 Sketch of subsidence-time curve of D1～18 points

深基坑影响范围由降水和开挖确定,计算边界取基坑开挖、围护结构受力后不再产生变形影响处边界。深度取150m,计算范围取以基坑中心为中心的600m×500 m×150 m。本场地土层概况如表1。

根据前人成果[8],浦东地区第一软土层变形特征以塑性变形为主,第二软土层、第一硬土层及砂层变形特征以弹性变形为主。所以数值模拟中第一软土层的土体本构采用下负荷面剑桥模型,第二软土层、第二硬土层及砂层采用弹性本构。下负荷面剑桥模型需要的材料参数为:λ:e-lnp空间中压缩曲线的斜率;κ:e-lnp空间中回弹曲线的斜率;M*:临界状态下的剪切应力比;e1:正常固结线在e轴上的截距;OCR:超固结比。模型计算参数可从土样室内试验得到。

各土层参数选取如下:第一软土层的压缩指数λ、回弹指数κ由魏道垛,胡中雄对上海浅层土的压缩性参数做了大量的试验研究[9],得到的试验参数见表2。

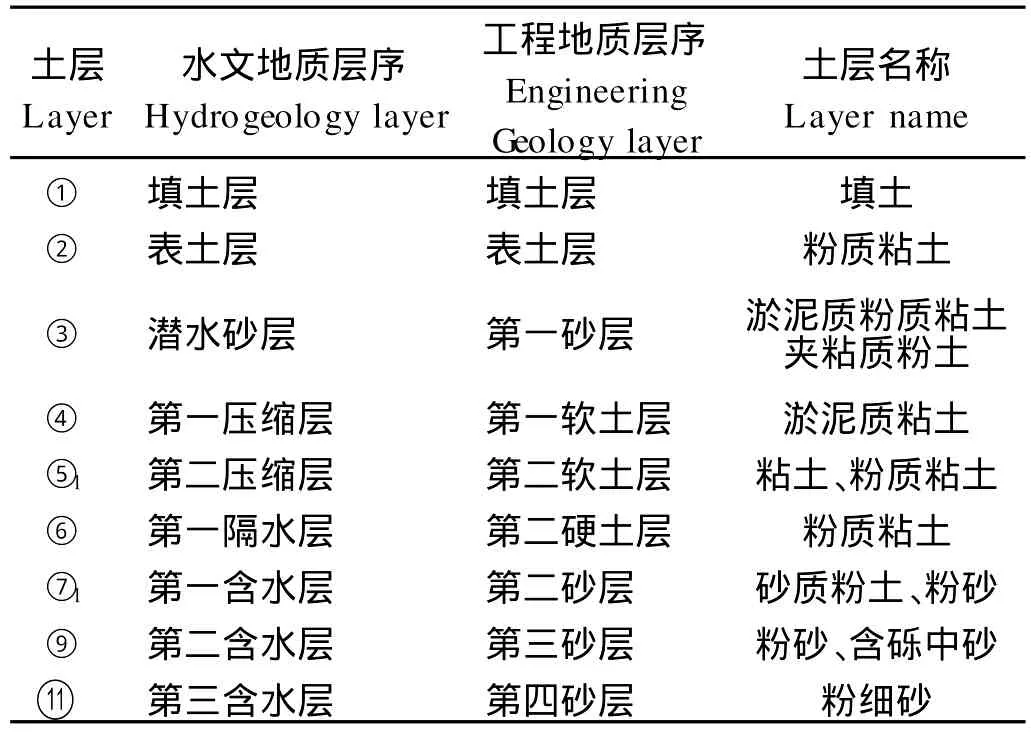
表1 土层地质概况Table 1 Geology conditions

表2 上海浅层土的压缩性参数表Table 2 The comp ressibility of Shanghai shallow soil

第一软土层:λ=0.110 5、κ=0.013 5、v=0.40、ein=1.1、γsat=1.7×104N/m3、k=1.08×10-7cm/s、a=500、e0=1.05;表土层、第一砂层、第二软土层、第二硬土层、第一、二、三含水层参数(见表3)。

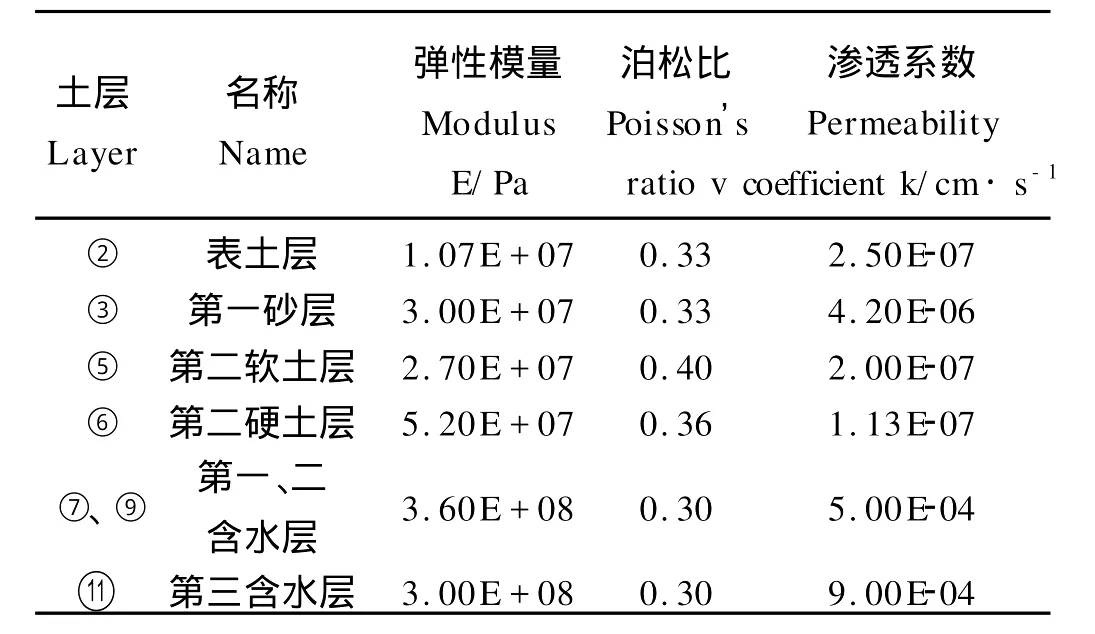
表3 弹性计算参数表Table 3 Elastic compute parameter

基坑围护系统中的地下连续墙选用实体单元,其参数参考相关文献[10],采用均质弹性模型,弹性模量为2.3×107Pa,泊松比为0.167。地下连续墙与土体间界面采用库仑摩擦类型,滑移类型选用小滑移,接触面无厚度,法线方向刚性,摩擦系数取0.3。

2.3.2 初始条件与边界条件 初始条件、边界条件和加载情况在求解时起了决定作用。本次模拟的力学边界条件:模型底面各向位移都为0,侧面各边界法向(水平向)位移为0,上表面(地面)为自由边界,无约束。渗流边界条件:计算域侧面为定水头边界,底面为不透水边界,初始水位假设在地表,每步开挖结束后基坑底面孔压为0。

2.3.3 单元类型及网格划分 计算范围确定以后,要对求解区域土体进行有限元划分。土与地下连续墙的单元类型采用耦合的平面应变单元CPE4P,地下连续墙用渗透系数几乎为0的平面应变单元来模拟。对基坑开挖部分附近处的网格进行了加密,并随距离的增加使网格由密变疏,模型被划分为9 000个单元。

2.3.4 计算模拟过程 依据实际工程的施工工况,考虑到基坑开挖的逐次性、途径依赖性和非线性[11],深基坑的施工过程中有很多不同的施工阶段,在卸载某阶段土的性质不仅与当前的应力状态有关,而且与应力路径有关,因此要得到正确的计算结果,关键在于能否对深基坑开挖过程正确地模拟。在岩土工程界常用的几种数值分析方法主要包括:有限元法、有限差分法、边界元法、离散元法、数值流形法等[12],本文采用有限单元法。

确定土体的初始应力条件和位移条件是模拟基坑开挖的第一步,首先需要建立土的初始应力场。初始应力是距土层表面深度的函数,ABAQUS通过结合使用初始状态过程和地压平衡过程来建立初始应力场[13]。土体初始应力场建立以后,通过ABAQUS中移除和恢复单元或接触对的功能,来模拟基坑开挖中土体的移走和支撑的设置。在移除开挖部分以前,ABAQUS存储被移除区域对模型剩余部分的力,在移除中,这些力降为零,移除区域对剩余部分影响在移除步骤结束后完全消除。在整个开挖过程中,土体处于卸荷状态。

第二步为渗流场和应力场的耦合分析。在软土地区开挖基坑时,地下水渗流对基坑工程性状影响不容忽视,基坑开挖卸载在坑底和周围土体产生负的孔隙水压力,并随着每步开挖结束时暴露时间的增加而逐渐消散;同时,地下水在坑内外水头差的作用下发生渗流。所以在地下水位高时,基坑开挖将伴随着开挖卸载、坑内外水头差的变化、超静孔隙水压力消散的耦合过程,本文中计算考虑基坑开挖过程中土体变形和渗流的耦合作用,用ABAQUS对卸载和渗流作用下的基坑开挖进行分析。对应力场和渗流场的耦合问题求解一般分为两大类:序列耦合方法和直接耦合方法。序列耦合解法是按照顺序进行2次或更多次的渗流场与应力场分析。直接耦合解法利用包含所有必须自由度(位移和孔压)的耦合单元类型仅仅通过一次求解就能得出耦合场的分析结果。这种情况下的耦合是通过计算包含所有必须项的单元矩阵或单元载荷向量来实现。ABAQUS凭借其强大的非线性功能采用直接耦合方法,二维耦合单元包括CPE4P、CPE4PR、CPE8P、CPE8PR等单元,本文采用CPE4P。

2.3.5 计算结果

(1)地面沉降总体竖向变形云图

计算步骤按照工程实际工况(见图2),选取计算剖面A-A′,该剖面上有地面沉降观测点D4、D4-1、D4-2、D4-3、D4-4、D4-5、D4-6,选取计算剖面B-B′,该剖面上有地面沉降观测点D8、D8-1、D8-2、D8-3、D8-4、D8-5、D8-6。剖面A-A′和B-B′最后1个计算步的地面沉降云图见图11和图12,地面沉降在距基坑20 m处达到最大值,分别为22和26 mm。

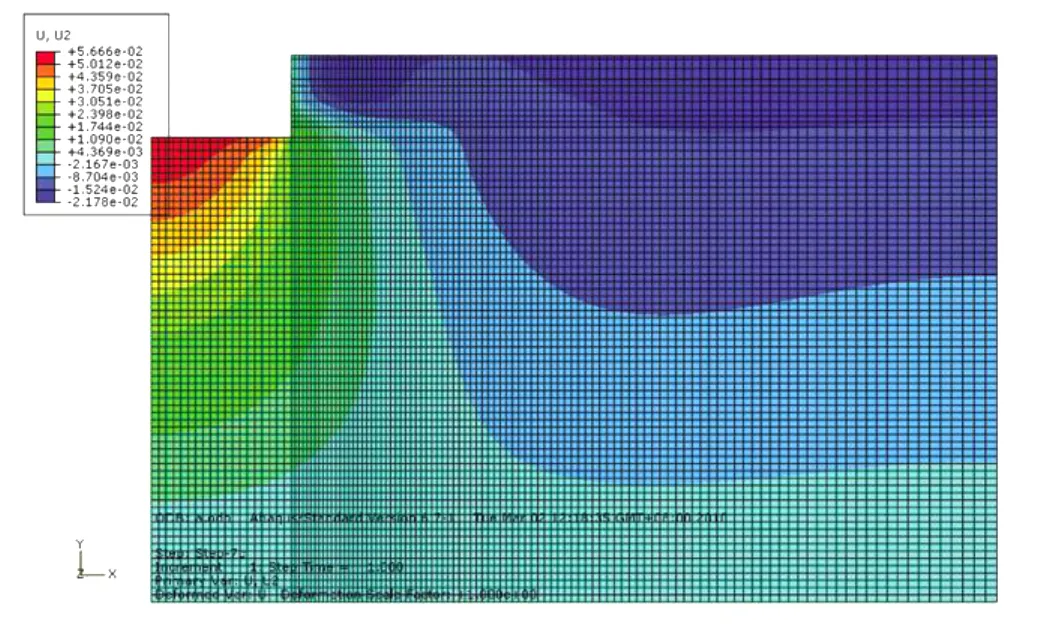
图11 基坑开挖剖面A-A′沉降模拟最终沉降云图Fig.11 Sketch of final subsidence sim ulation in p rofile A-A′

图12 基坑开挖剖面B-B′沉降模拟最终沉降云图Fig.12 Sketch of final subsidence simulation in profile B-B′

(2)地面沉降观测点实测值与计算值的对比

表4 观测点最后沉降量计算值与实测值比较表Table 4 Calculated and measured value of the final settlement

本次观测点最后地面沉降计算值与实测值最大误差不超过20%(见表4),地面沉降观测点实测值与计算值拟合较好,证明参数选取合理,下负荷面剑桥本构模型能较好地反映计算区的地面沉降特征。

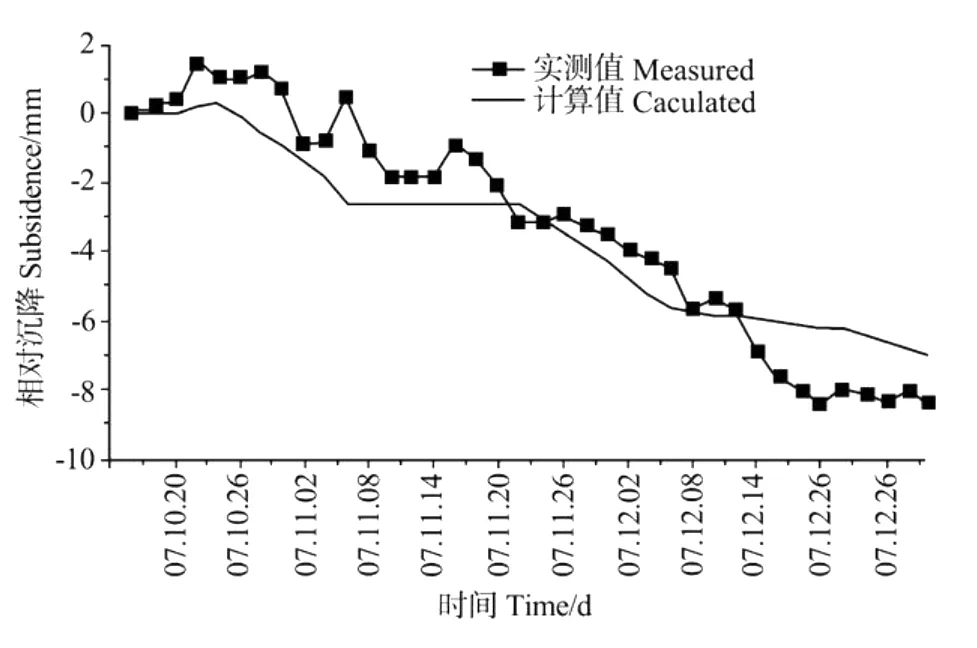
图13 地面沉降观测点D4-4实测值与计算值对比曲线Fig.13 Comparison of D4-4 measured and calculated curve

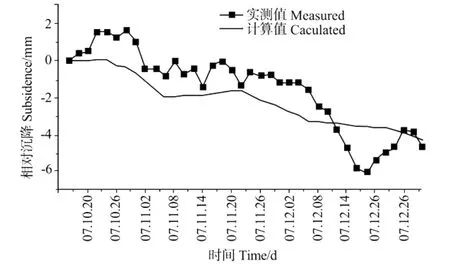
图14 地面沉降观测点D4-6实测值与计算值对比曲线Fig.14 Comparison of D4-6 measured and calculated curve

图15 地面沉降观测点D8-4实测值与计算值对比曲线Fig.15 Comparison of D8-4 measured and calculated curve

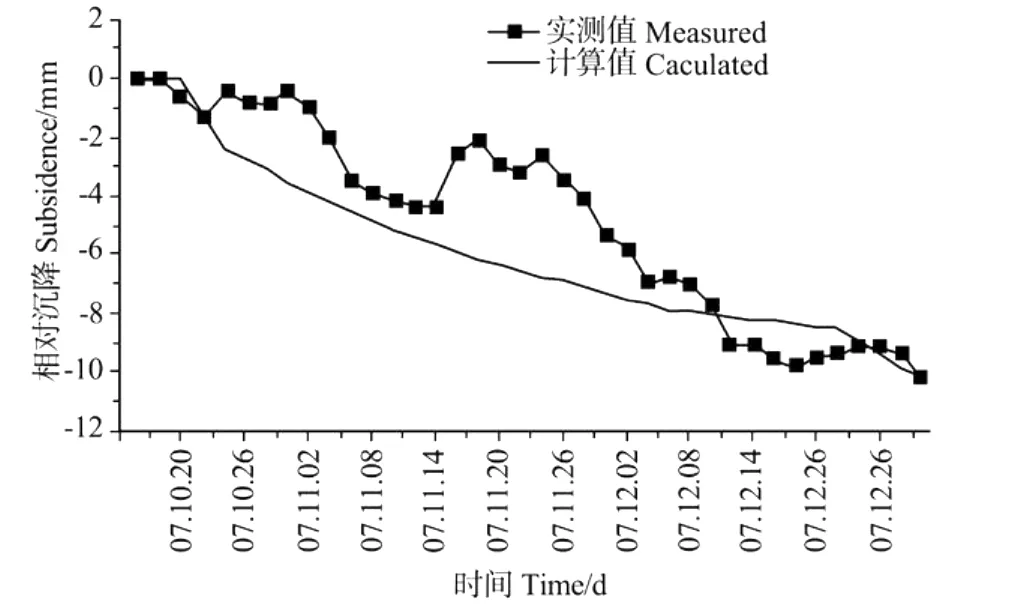
图16 地面沉降观测点D8-6实测值与计算值对比曲线Fig.16 Comparison of D8-6 measured and calculated curve

(3)地面沉降随开挖后发展变化

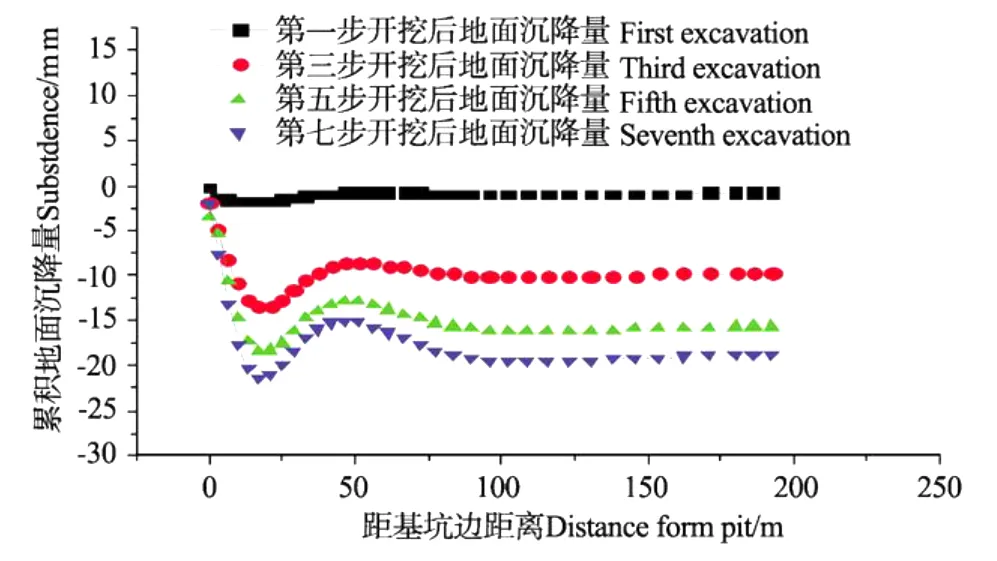
图17 剖面A-A′地面沉降量Fig.17 Sketch of section A-A′land subsidence

图18 剖面B-B′地面沉降量Fig.18 Sketch of section B-B′land subsidence

剖面A-A′在不同开挖步时地面沉降分布不同(见图17),随着开挖深度加大,坑后地面沉降量在增加,最大地面沉降量23 mm产生在最后一个开挖深度时在离开坑边20 m左右的位置。剖面B-B′在不同开挖步时地面沉降分布见图18,随着开挖深度加大,坑后地面沉降量在增加,最大地面沉降量27 mm产生在最后一个开挖深度时在离开坑边24 m左右的位置。

3 结论

(1)下负荷面剑桥模型形式简单,物理意义明确,不仅描述了超固结特别是重超固结黏土的力学特性,如体积剪胀,应变软化等,而且描述了循环荷载下土体应力应变特性的能力。

(2)深基坑工程的地面沉降,来自于地下水位下降导致的土体固结压缩和基坑开挖引起的基坑周围应力差和剪应变两方面,而承压含水层的降压引起的沉降效应最为明显;人工回灌法通过注水使承压含水层水位上升引起粘土层回弹从而控制降水引发的工程性地面沉降,是一种行之有效的方法。

(3)如何确保基坑周围原有建筑物、构筑物、地程中坑周环境保护的首要工作[14]。盛大基坑的水位实测资料表明施工中的承压水水位均达到设计要求,地下水回灌开始后水位降深速率明显变小,根据地面沉降监测资料,地面沉降的下降幅值主要受开挖深度的影响,开挖深度越深,地面沉降越大,回灌开始后地面沉降速率减缓,说明坑外人工回灌对水位下降有控制作用。

(4)地面沉降的下负荷面剑桥模型数值模拟结果显示基坑周围的地面沉降到达最大值后会随着距离的减小而减小最后趋于稳定。数值模拟的结果验证了下负荷面剑桥模型能较好地反映计算区的地面沉降,与实际水位和地面沉降数据较吻合,对类似工程降水设计和施工具有推广价值。

[1] Asaoka A,Noda T,Yamada E,et al.An elastop lastic descrip tion of two distinct volume change mechanism s of soils[J].Soils and Foundations,2002,42(5):47-57.

[2] Hashiguchi K,Ueno M.Elastop lastic constitutive law s of granular material[C].Constitutive Equations of Soils.Tokyo,JSSM FE:1977.

[3] Hashiguchi K.Constitutive equations of elastoplastic materials with elastic-plastic transition[J].Journal of Application Mechanics,1989,47:266-272.

[4] Nakai T,Hinokio M.A simple elastoplastic model for normally and over consolidated soils with unified material parameters[J].Soils and Foundations,2004,44(2):53-70.

[5] 张锋,叶冠林.计算土力学[M].北京:人民交通出版社,2007.

[6] 黄雨,周子舟.下负荷面剑桥模型在ABAQUS中的开发实现[J].岩土工程学报,2010,32(1):115-119.

[7] Hashiguchi K.Subloading surfacemodel in unconventional plasticity[J].International Journal of Solids and Structures,1989,25:917-945.

[8] 叶淑君,薛禹群,张云,等.上海区域地面沉降模型中土层变形特征研究[J].岩土工程学报,2005,27(2):140-147.

[9] 魏道垛,胡中雄.上海浅层土的前期固结压力及其有关压缩性参数的试验研究[J].岩土工程学报,1980,2(4):13-22.

[10] Duncan JM,Hashash M A,Whitman R V.Analysisof deep excavation in Boston[J].Journal of Geotechnical Engineering,1993,119(1):69-90.

[11] 俞建霖,龚晓南.基坑工程的性状分析[J].岩土工程学报,1999,21(1):21-25.

[12] 何满潮.工程地质数值法[M].北京:科学出版社,2006.

[13] 徐方京,谭敬慧.地下连续墙深基坑开挖综合特性研究[J].岩土工程学报,1993,15(6):28-33.

[14] 卢礼顺,刘建航,刘庆华.上海某地铁车站深基坑周围土体沉陷研究[J].岩土工程学报,2006,28:17-23.