胶州湾潮汐潮流高分辨率数值模拟研究*

陈金瑞,陈学恩,于华明,闫运伟,单士亮,赵 健

(中国海洋大学海洋环境学院,山东青岛266100)

近年来,随着数值模式的完善和超级计算能力的形成,使对区域海洋进行高分辨率数值模拟研究成为可能。对胶州湾及近海的潮汐、潮流变化开展高分辨率数值模拟研究,不仅可以认识胶州湾及近海自身环流结构的特征与变化,胶州湾与黄海的相互影响,湾内污染物的扩散输运,泥沙的输运和沉积等科学问题;更有着指导港口航运,港口建设,水产养殖,近岸海上运动等实用价值。

胶州湾位于黄海之滨,山东半岛的南岸,以团岛头(36°02′36″N,120°16′49″E)与薛家岛脚子石(36°00′53″N,120°17′30″E)连线为界,是一个与黄海相通的半封闭式海湾。海湾东西宽27.8 km,南北长33.3 km;湾口开向东南,口门最窄处为3.1 km,岸线长187 km,平均水深约7 m,最大水深64 m。迄今,前人对胶州湾潮汐潮流的数值模拟研究做出卓有成效的工作[1-9],例如,闫菊等[4]曾模拟了胶州湾M 2分潮的潮汐潮流变化,给出了潮致余流的水平结构;孙英兰等[5]基于ECOM模式,引入变边界处理技术,指出潮流的量值及最大流发生时刻随深度增加而减小,在底层附近,减小比率较大,主要是因为底摩擦的作用;高大鲁等[8]利用POM模式对胶州湾进行的多个分潮的潮位和潮流模拟,讨论了胶州湾的潮位、水平流速和垂直流速的性质;吕新刚等[9]从能量的角度探讨了潮波的传播特性,并且讨论了漫滩过程对潮流模拟的重要性;赵亮等[7]利用ECOM对胶州湾潮波系统及其驱动下的标识质点运移规律进行数值模拟,指出胶州湾平均水存留时间为80 d,不同的区域水交换能力相差较大。然而,由于胶州湾地形和岸线条件复杂,受当时计算机性能的限制,上述数值研究采用的模式网格较粗,对岸线和底形的分辨率不够高,故其所提供的该区的潮汐潮流分布信息不够细致。

本文应用Finite-Volume Coastal Ocean Model(FVCOM)模式[10],采用2008年的最新岸线地形,设计高分辨率的三角形网格,考虑漫滩效应,用以研究胶州湾潮汐潮流的精细化结构及其时空分布规律。

1 模型配置和验证

FVCOM陆架海洋模式的特点是,在水平方向上采用非结构化三角形网格,垂向采用σ坐标变换,数值方法采用有限体积方法,通过积分三角形控制体通量来解控制方程,将有限元拟合曲折岸线的优点与有限差分方法高效计算的优点结合起来,并且对于近岸、河口等具有复杂地形和岸线的区域来说能更好地保证质量、动量的守恒性。另外,FVCOM还包含三维干/湿网格处理等模块。本文采用FVCOM对胶州湾进行数值模拟研究。对于像胶州湾这样1个具有海底地形复杂,滩涂面积大,岸线弯曲不规则,潮差较大的海湾,选择FVCOM模式进行水动力模拟是非常适合的。

1.1 模型配置

为从数值上再现胶州湾近岸海域潮汐潮流,本文研究区域设定为120.00°E～121.20°E,35.50°N～36.50°N。模式的水深资料来自中华人民共和国海事局出版的海图,湾内的水深主要取自2008年的海图数据。结合FVCOM的特点,本文对胶州湾口岸线变化复杂及水深坡度较大的区域和一些较小的岛屿进行了网格加密(见图1)。模型水平采用无结构三角形网格系统,垂向分7个σ层,计算区域内共有25 956个网格节点(node),49 729个三角形单元(cell),最小网格步长为50 m,模型外模积分步长为0.8 s,内模步长为4 s。从图1中可见,三角形网格较好地概括了计算域内复杂的岛屿岸线和地形特征,对复杂岸线的拟合较为精确。对于水平湍流混合系数,FVCOM中采用了Smago rinsky涡动参数化方案。

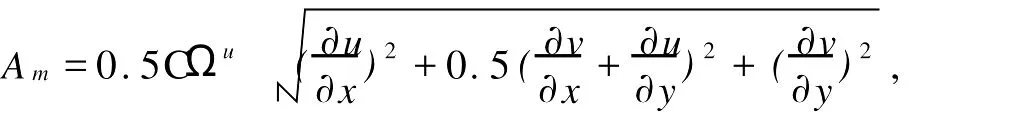
式中:C为常数,Ω为每个三角形网格的面积。

图1 胶州湾模式的计算范围和计算网格Fig.1 Calculation range and mesh in Jiaozhou Bay

1.2 边界条件

本文主要进行数值诊断研究,不考虑温盐变化,温盐设为常数,32 PSU和20℃;也不考虑大气对海洋的影响。模式采用零初始条件(t=0时,U=V=η=0),潮位和流速均设为0。开边界的73个节点采用8个主要天文分潮(M 2、S2、N2、K2、K1、O1、P1、Q1)的调和常数,然后利用t_tide软件后报出开边界的水位,来驱动本文的数值模式。调和常数采用OTIS(OSU Tidal Inversion Software)数据,并融合胶州湾近海的历史同潮图数据。数值积分时间跨度为35 d,2008年7月25日～2008年8月31日。

图2 胶州湾海域的水深(m)和水位潮流验证点分布Fig.2 Distribution of water dep th and observation stations in Jiaozhou Bay

1.3 模型验证

本文选取青岛五号码头和小麦岛验潮站2008年8月1日00··00～2008年8月30日23··00的逐时观测资料(见图3),来验证数值结果,水位对比曲线表明二者吻合较好。五号码头和小麦岛2个站位的模拟值与观测值后报的潮位的平均绝对误差均在10%以内。表1给出了2个潮位验证点的振幅和迟角对比,除了S2和K1的迟角偏差稍大,M 2、N 2、O1分潮模拟与实测结果吻合较好,模拟精度可以接受。

图3 五号码头和小麦岛潮位模拟与实测值比较Fig.3 Comparison between the observed and computed tidal elevation at Xiaomaidao and Wuhaomatou

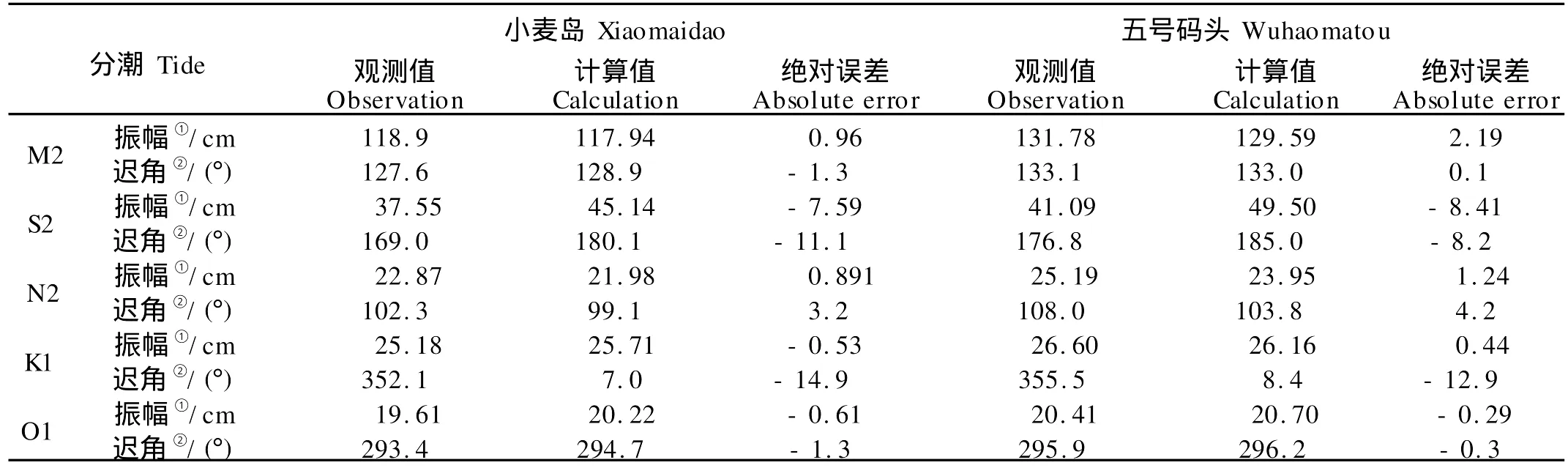
表1 观测与计算的调和常数对比表Table 1 Comparison between the observed and computed tidal constituent

综上所述,通过对流速流向对比表明,本文所建立的胶州湾潮流模式是可信的,模拟结果能较好地体现胶州湾海域的潮汐潮流特征。

2 结果分析

2.1 潮汐分析

图4给出了胶州湾的潮汐性质判别数,胶州湾及湾口近海的潮汐性质判别数介于0.35～0.40之间,属规则半日潮,该海区半日潮占优。对模拟结果的调和分析表明(见图5),胶州湾M 2、S2、K1、O1分潮波都主要从外海传入,均不构成完整独立的潮汐系统。在胶州湾外,分潮波自东北向西南沿逆时针方向传播,振幅由外海向湾内增大。湾口与湾顶M 2分潮的振幅差约10 cm,4个分潮的潮汐最大振幅分别为1.34、0.51、0.262、0.208 m。

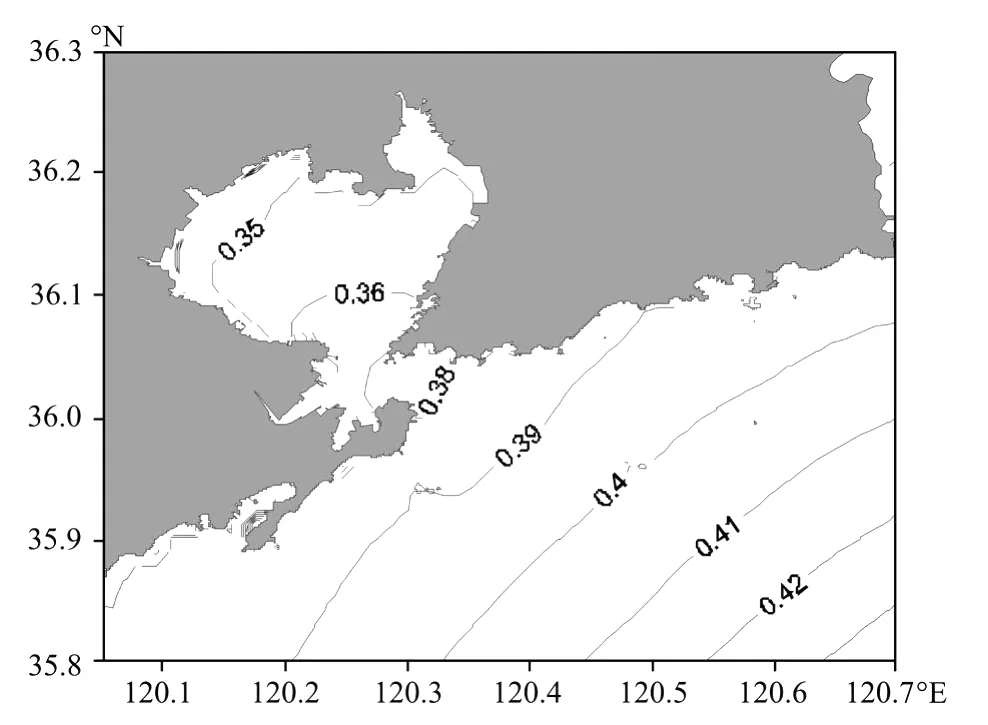
图4 胶州湾海域潮汐性质Fig.4 Distribution of calculated tidal characteristics in Jiaozhou Bay

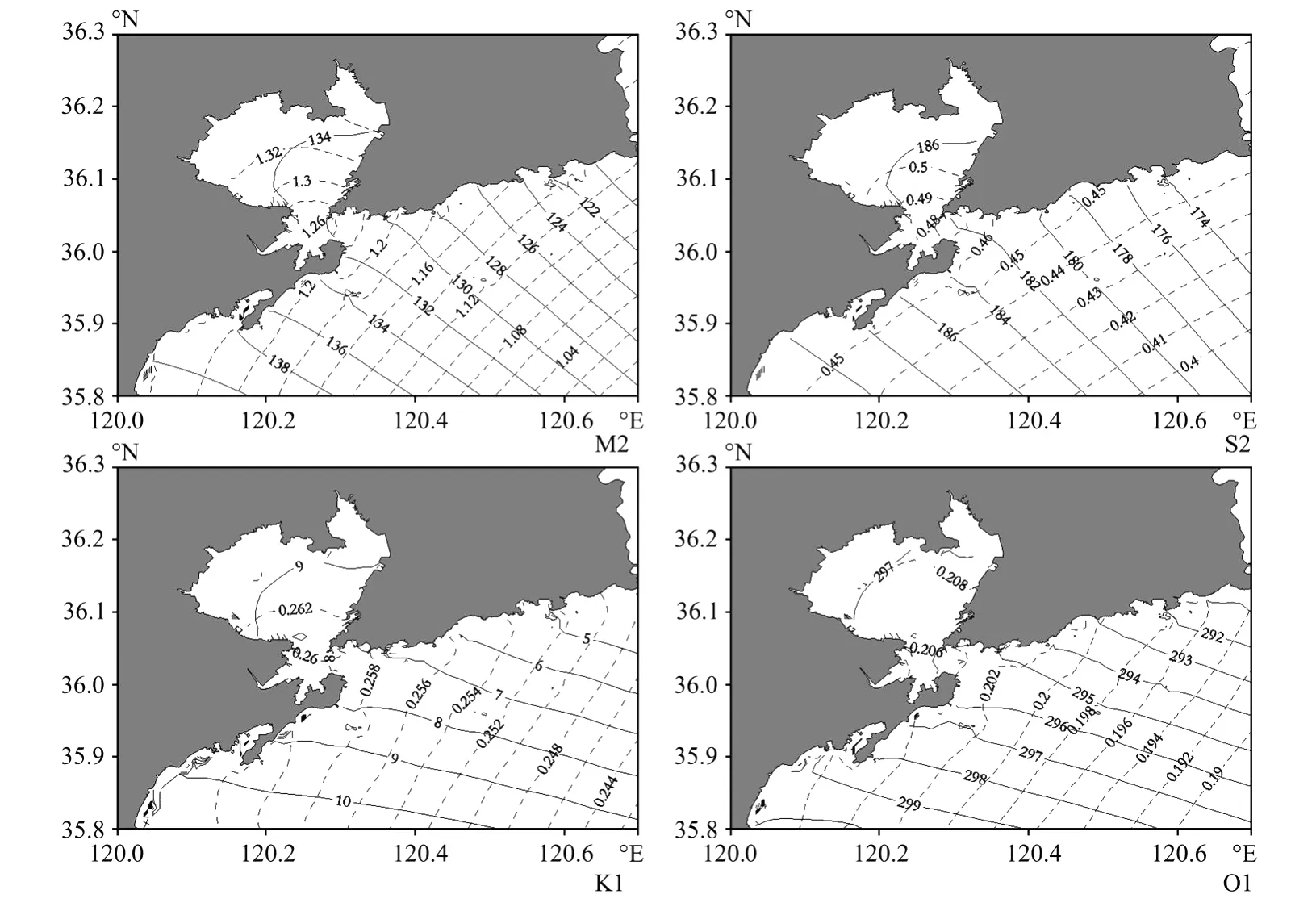
图5 胶州湾海区分潮同潮图Fig.5 Sketch map of co-tidal lines in Jiaozhou Bay

2.2 潮流分析

对数值结果计算表明,胶州湾海域潮流类型判别数介于0.2～0.3之间,也具有规则的半日潮流的性质。图6给出了小麦岛水文站大潮时段的涨落急时刻潮流分布图,外海的海水偏西向进入胶州湾外湾口后分叉:一支偏西南向进入黄岛前湾和海西湾;主流绕过团岛咀,偏西北向进入胶州湾内湾口再分叉:一支北偏东向进入沧口水道;一支北偏西向,由中沙礁西侧进入内湾;余部由中央水道北进[14],涨、落潮最大流速均发生在胶州湾湾口。

图7给出了研究区域M 2、K1分潮的表层潮流椭圆水平分布(红线:顺时针旋转;黑线:逆时针旋转)。从图7a可以看出,在湾外,M 2和K1分潮的潮流椭圆旋转率较大,以旋转流为主,潮流椭圆主要呈逆时针方向旋转;在湾内则主要呈顺时针方向旋转;由于湾口附近岸线复杂和水深坡度大,潮流以往复流为主,潮流椭圆的旋转方向变化复杂。湾口及湾内,潮流椭圆旋转率较小且为负值,以往复流为主。各个分潮的椭圆长轴最大值都出现在湾口附近的水道上,M 2、S2、K1和O1的最大椭圆长轴分别为1.13,0.41,0.126和0.12 m/s。

图6 大潮涨落急时刻的潮流分布Fig.6 Distribution of tidal current

图7 潮流椭圆分布Fig.7 Distributions of tidal current ellipse

2.3 最大可能流速

最大可能流速由对模拟结果进行调和分析所得的调和常数来计算,对于规则半日潮海区,最大可能流速的算式为[11]:

其中WM2、WS2、WK1、WO1分别为M 2、S2、K1、O1分潮潮波的潮流椭圆长半轴。根据上述公式,计算胶州湾海域的最大可能流速,绘制最大可能流速分布于图8,从图8可以看出,最大可能流速分布基本与等深线一致,与岸线平行。在胶州湾内最大可能流速介于0.5～0.9 m/s之间,湾口处因应岸线和地形变化,最大可能流速的变化梯度较大,最大可能流速可达2.14 m/s。

图8 最大可能流速分布图Fig.8 Distributions of maximum probable current velocities

2.4 潮致余流

潮致欧拉余流速度是指海域内某一确定点在1个潮周期内潮流速度的时间平均值,它表示在确定位置上流体周期平均的迁移趋势,因在浅海中潮流的非线性项受到侧向岸线和底摩擦的作用,一部分周期性能量会转变成非周期性能量。余流的大小与地形和岸线有密切的联系。根据模式的结果计算潮致余流(见图9),在湾口处,由于岬角地形和岸线的共同作用,水平结构显著地表达为“团团转”的多涡结构[4],在团岛咀处的岬角锋,形成4个主要涡旋环流系统(A、B、C、D),且潮汐余流的最大流速在团岛附近可达0.43 m/s,与吕新刚等[9]根据实测资料推算所得团岛嘴西侧近岸水域最大潮余流0.5 m/s吻合。除了这4个强环流系统[4、9],本研究在胶州湾中部,由于模式精度的提高,还首次揭示了2个相对较弱的余环流系统(E和F),流速小于0.1 m/s。

图9 胶州湾的余流场Fig.9 Distribution of residual currents in Jiaozhou bay

2.5 潮流能通量

为反映胶州湾及其近海潮汐能的分布和传播,本文通过潮流能通量来估算潮流能[12-13]:

P潮流能通量,ρ密度,g重力加速度,U体积输运矢量,v流速,H水深,ζ水位,<>代表时间平均。潮流能通量不仅可以反映潮流能量的分布,而且可以反映潮流能量的传播。结果表明(见图10),胶州湾外海海区的潮流能通量主体自东北向西南方向传播,基本上沿岸线;在接近湾口时,一部分潮流能沿着海岸线继续向西南传播,另一部分潮流能向湾口汇集并继续向湾内传播,经过湾口,潮流能由汇聚转为发散,传向内湾。湾口附近由于地形和岸线的共同作用,潮流能通量在内外湾口分别做顺时针旋转,呈“左进右出”的结构。潮流能通量在内外湾口“左进”的量值比较大,“右出”的量值比较小,湾口附近存在1个潮能通量的高值区,这是因为,湾口水深梯度较大和岸线共同导致流速较大,进而潮流能通量也较大。内湾大部分区域潮能通量比较弱。

图10 胶州湾的潮流能通量的水平分布Fig.10 Horizontal distribution of tidal energy flux in Jiaozhou Bay

2.6 海湾纳水体积与纳潮量的计算

纳潮量是表征半封闭海湾生命力的重要指标,其大小直接影响到海湾与外海的海水交换强度和污染物的迁移扩散,从而制约着海湾的自净能力和环境容量,对于维护海湾良好的生态环境至关重要,纳潮量的变化直接影响到海湾的潮流特性,还可能打破水动力条件与海湾形态之间的动态平衡,使海湾槽滩形态随之进行调整。海湾面积的减小会造成纳潮量的减小。

根据模式的计算结果,分析纳潮量列于表2。结果表明,团岛-黄岛油码头以内(内湾)的海域面积为3.09亿m2,平均纳潮量为7.36亿m3;团岛-薛家岛以内(外湾加湾口)的海域面积为3.487亿m3,平均纳潮量为8.31亿m3。

2.7 Dye浓度的扩散

为分析内湾与外湾的水交换,本文设计了数值染色实验来直观地反应水体交换情况。

在数值模式中采用下述浓度扩散方程:

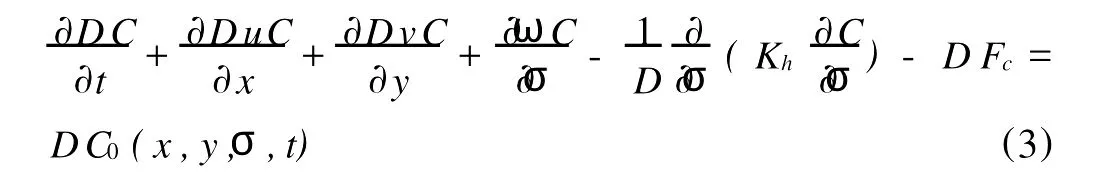
其中,C染色实验的浓度,D总水深,u、v和ω为流速的分量,Kh垂直热扩散系数,Fc水平扩散项,C0为初始浓度或者点源的浓度。

取团岛、薛家岛之间的连线作为内、外湾分界线,将内湾初始污染物浓度设置为1,外湾初始污染物浓度设为0,模式其它设置与水动力配置完全相同,进行污染物扩散数值模拟实验。图12b给出了数值积分30 d后内湾污染物浓度的分布:30 d后,内湾余留污染物的平均浓度为63.2%,即30 d的水交换率为36.8%,可估算湾内整体水交换约需要82 d(30÷36.8%≈82),这与赵亮等[7]胶州湾平均水存留时间80 d这一结论吻合。

表2 大小潮胶州湾水体体积和纳潮量Table 2 The volume of water and tidal prism of Jiaozhou Bay at spring and neap tidal/亿m3

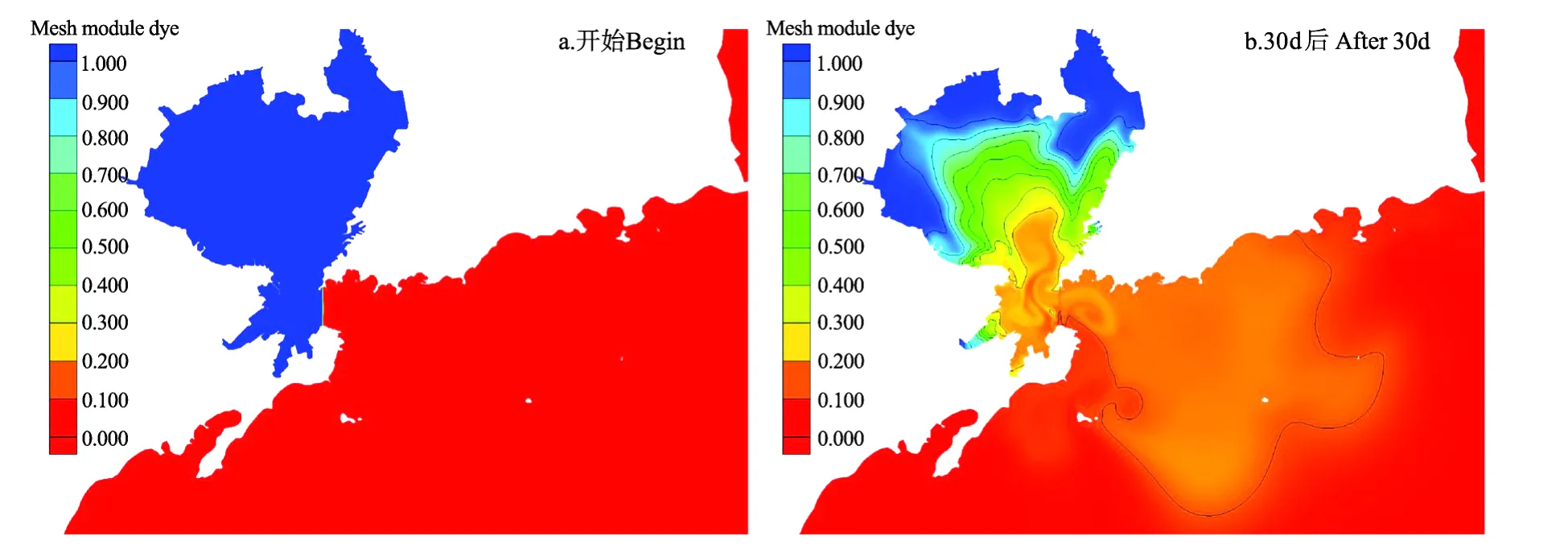
图11 污染物浓度分布Fig.11 Distributions of dye

3 结论

本文基于三维变边界水动力模型FVCOM,考虑8个主要天文分潮,对胶州湾及其近海海域的潮汐、潮流进行了高精度的数值模拟研究,三角形网格很好地拟合了不规则岸线,高精度地刻画了较小尺度的岛屿和复杂岸线,提高了模式的模拟精度,干湿网格技术处理漫滩问题,使潮汐潮流的模拟结果更加可靠。

在结合历史观测资料和前人工作,对模式进行对比验证的基础上,揭示了胶州的潮波主要特征:

(1)胶州湾的潮汐类型为属于规则半日潮。湾外分潮的潮流椭圆旋转率较大,以旋转流为主,逆时针方向旋转;在湾口及湾内,潮流椭圆旋转率较小且为负值,往复流为主,各个分潮的椭圆长轴最大值都出现在湾口附近的水道上,M 2、S2、K1和O1的最大椭圆长轴分别为1.13、0.41、0.126和0.12 m/s。

(2)高精度的数值模拟揭示了6个较大的潮汐余环流系统,余流最大值达0.43 m/s;本研究还在胶州湾中部首次揭示了2个相对较弱的余环流系统(E和F),流速小于0.1 m/s。胶州湾的最大可能流速的分布基本与等深线一致,最大值可达2.14 m/s。

(3)湾口附近由于地形和岸线的共同作用,潮流能通量在内外湾口分别做顺时针旋转,呈“左进右出”的结构,从外湾口进入的潮波能量有41.7%耗散在内外湾口之间的海区。

(4)纳潮量研究结果表明,胶州湾的平均纳潮量为8.31亿m3,染色试验表明,胶州湾30天的水交换率为36.8%。

致谢:在本文研究过程中,作者们还得到中国海洋大学海洋环境学院计算中心的支持,在此表示感谢。

[1] Chen Changsheng,Ji Rubao,Zheng Lianyuan.Influencesof physical p rocesseson the ecosystem in Jiaozhou Bay:A coupled physical and biological model experiment[J].J Geophys Res,1999,104:29925-29949.

[2] 王化桐,方欣华,匡国瑞,等.胶州湾环流和污染扩散的数值模拟Ⅰ胶州湾潮流数值计算[J].中国海洋大学学报:自然科学版,1980,10(01):26-63.

[3] 鲍献文,闫菊,赵亮,等.ECOM模式在胶州湾潮流计算中的应用[J].海洋科学,1999,(05):56-60.

[4] 闫菊,王海,鲍献文.胶州湾三维潮流及潮致余环流的数值模拟[J].地球科学进展,2001,16(02):172-177.

[5] 孙英兰,张越美.胶州湾三维变动边界的潮流数值模拟[J].海洋与湖沼,2001,32(04):355-362.

[6] 孙长青,王学昌,孙英兰.填海造地对胶州湾污染物输运影响的数值计算[J].海洋科学,2002,26(10):47-50.

[7] 赵亮,魏皓,赵建中.胶州湾水交换的数值研究[J].海洋与湖沼,2002,33(01):23-29.

[8] 高大鲁,魏泽勋,华锋.胶州湾多分潮漫滩数值模拟研究[J].海洋科学进展,2007,25(02):131-138.

[9] 吕新刚,乔方利,夏长水.胶州湾潮汐潮流动边界数值模拟[J].海洋学报,2008,30(04):21-29.

[10] Chen Changshen,Huang Haosheng,Beardsley Robert C,et al.A finite volume numerical approach for coastal circulation studies:Comparisons with finite difference models[J].Journal of Geophysical Research,2007,112(C03018):1-34.

[11] 宋德海,鲍献文,朱学明.基于FVCOM的钦州湾三维潮流数值模拟[J].热带海洋学报,2009,28(02):7-14.

[12] Garrett C.Tides in gulfs[J].Deep-Sea Research,1975,22:23-35.

[13] Zu Tingting,Gan Jianping,Erofeeva Svetlana Y.Numerical study of the tide and tidal dynamics in the South China Sea[J].Deep-Sea Research,2008,55:137-154.

[14] 中国海湾志编纂委员会.中国海湾志第四分册(山东半岛南部和江苏省海湾)[M].北京:海洋出版社,1993:448.