带Hardy－Sobolev项的p－Laplace方程解的存在性＊

赵元章，严先微，张 强

（1.中国海洋大学数学科学学院，山东青岛266100；2.潍坊科技学院，山东潍坊261000）

带Hardy－Sobolev项的p－Laplace方程解的存在性＊

赵元章1，严先微1，张 强2

（1.中国海洋大学数学科学学院，山东青岛266100；2.潍坊科技学院，山东潍坊261000）

本文利用对称性临界点原理，在无界的柱形区域上，得到一类带Hardy－Sobolev项的p－Laplace方程的非平凡解的存在性。所得结果推广补充了已有的结论。

p－Laplace方程；山路引理；对称性临界点原理

0 引言

考虑如下的带Hardy－Sobolev项的椭圆型方程弱解的存在性问题

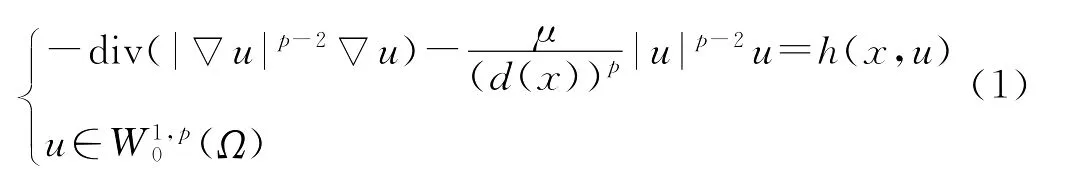
问题（1）有2个显著的特点：其一是区域是无界的，这导致空间（Ω）到Lα（Ω的嵌入不具有紧性，因而在利用临界点理论研究该问题的时候会产生本质上的困难；其二是Hardy－Sobolev项中的d（x）可能为0，方程具有奇异性。当μ＝0时，文献［1］利用集中紧性原理［2］讨论了问题（1）的解的存在性，文献［3］利用对称性环绕定理讨论了问题（1）的解的存在性；当μ≠0时，非线性项h（x，u）＝f（u）与变量x无关时，利用集中紧性原理，文献［4］给出了问题（1）的非平凡解的存在性。本文中，当非线性项h（x，u）与变量x有关时，利用对称性临界点理论，得到问题（1）的非平凡解的存在性，推广和补充了文献［4］中的相应结果。记

作如下的假设条件：

（1）f∶Ω×R→R连续，且存在常数c及α∈（p，p＊）使得

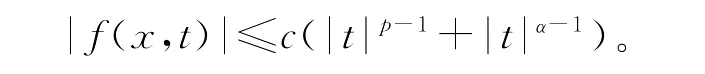
本文的主要结论如下：

定理1 在假设条件（1）～（5）之下，问题（1）存在非平凡的弱解。

1 预备知识

定义1［5－6］设X是Banach空间，G是紧拓扑群，U（X）为空间X上的等距在上的线性算子全体。设T∶G×X→X，若T连续，且满足下述条件

则称T为G在X上的一个等距在上的线性表示。

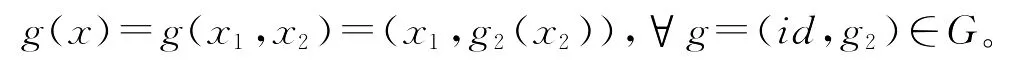
定义3［5－6］G在上的作用如下定义

记

引理1［7］当1＜p＜N，p＜α＜p＊时，X1到Lα（Ω）中的嵌入是紧的。

同时在Banach空间上存在如下形式的对称临界性原理。

引理2［8］（Banach空间中的对称临界性原理） 设X是Banach空间，G是紧拓扑群，是G在X上的等距在上的线性表示，是T（G）－不变泛函。若u是φ在Fix（G）上的临界点，那么u也是φ在X上的临界点。

注1 引理2可用到如下的特别情形：

引理3（山路引理［9］） 设X是Banach空间，f∈C1（X，R），且f满足

（a）.（P.S.）c条件，即对任意，如果满足

那么｛un｝中有收敛的子列；

则f有不小于a的临界值。

2 主要结果的证明

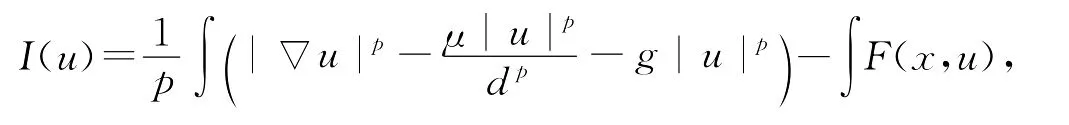
需要指明的是，在假设条件下，成立

I（u）∈C1（X，R）［4］，且对v∈X，有问题也就归结为求I（u）在X上的临界点。

由于无界区域Ω上X到Lα（Ω）的嵌入不具有紧性，故直接在X上利用山路引理求临界点具有一定的困难。条件（2）保证I（u）在X1上是G－不变泛函。由引理1、2，可以在X1上求I（u）的临界点，即也是I（u）在X上的临界点。

由于在柱形区域上，成立下述的不等式［10］

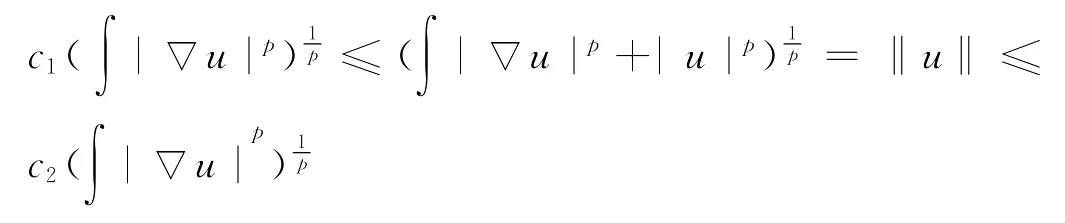
这里c1，c2＞0是常值。再由条件（5）和假设，故在X1上定义范数

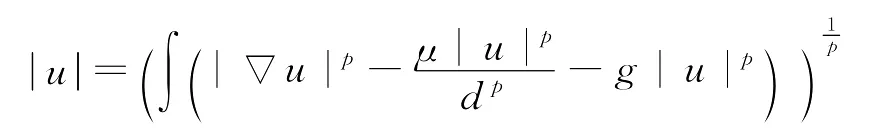
下面证明I（u）在X1上满足山路引理的条件。引理4 在假设之下，I（u）在X1上满足（P.S.）c条件。证明 设｛un｝X1是（P.S.）c序列，即

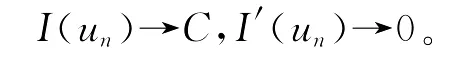
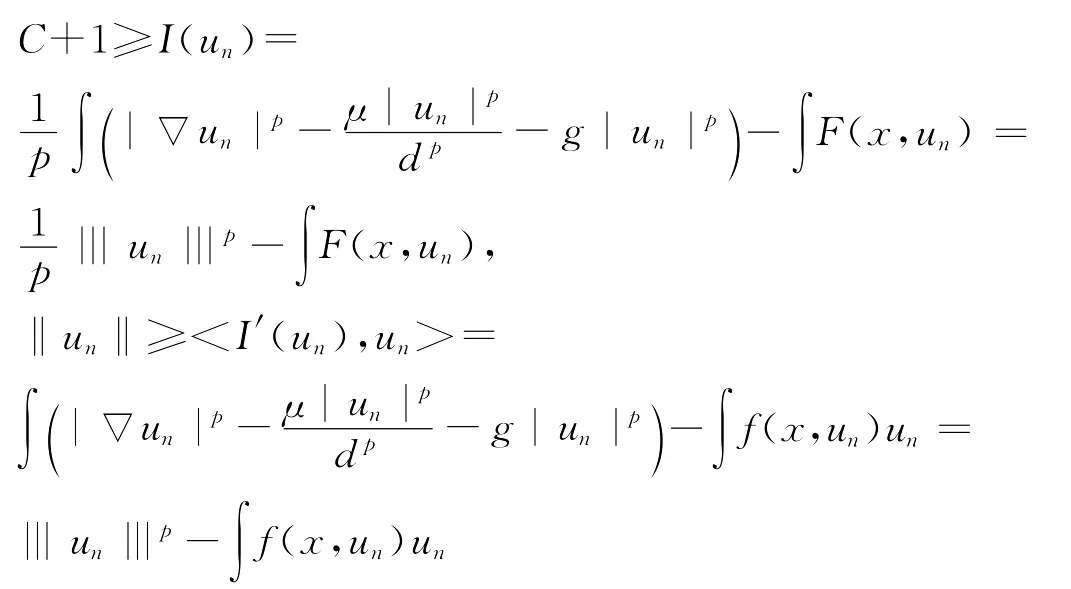
这样就由I（un）→C，I′（un）→0和条件（4）得到

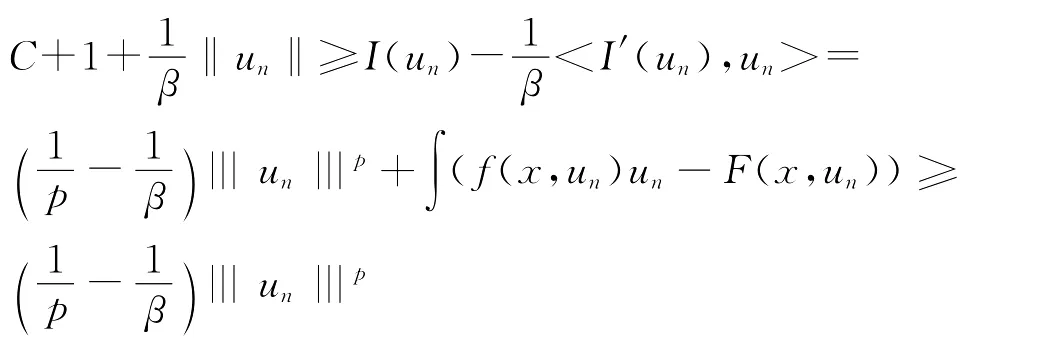
对任意的x，y∈RN，有下述不等式［11］

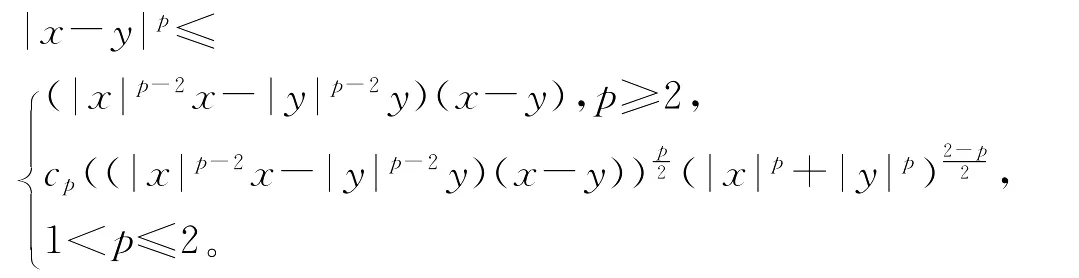
因此（以p≥2为例），

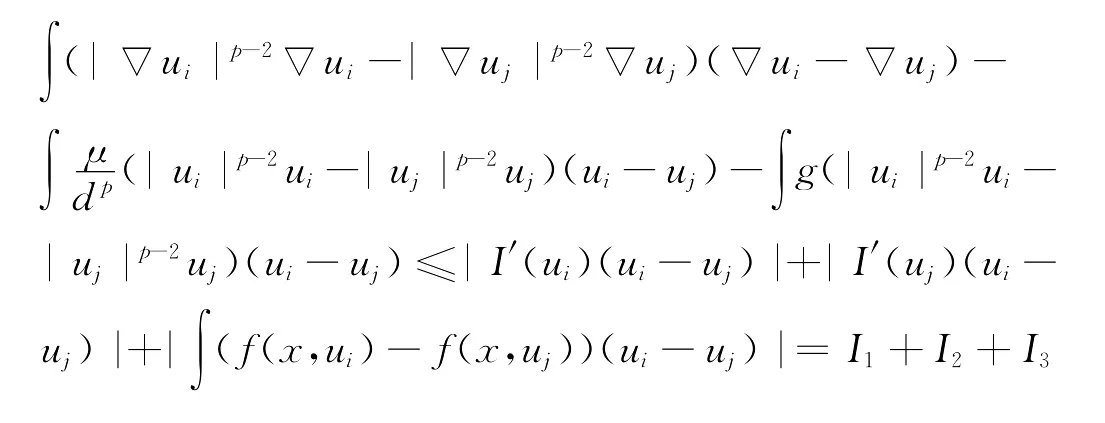
引理5 在假设下，I（u）满足引理3中的条件（b）。证明 由条件假设（1），得I（0）＝0。

由条件（1）、（3），得到对任意ε＞0，存在Cε＞0，使得

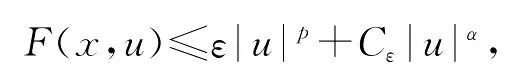
结合嵌入不等式得到

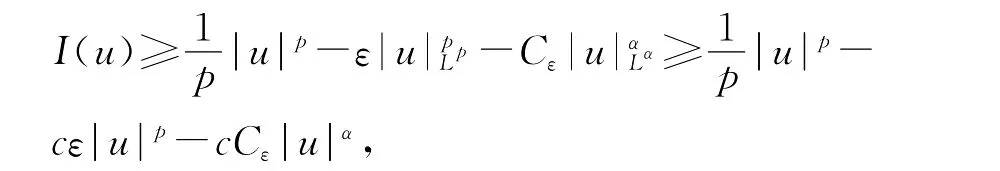
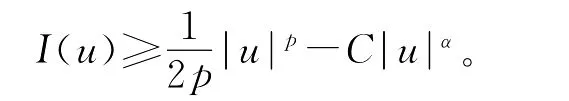
又α＞p，故当ρ＞0充分小时，存在a＞0，使得对任意的｜u｜＝ρ，成立不等式I（u）＞a＞0。

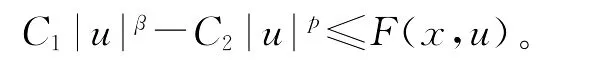
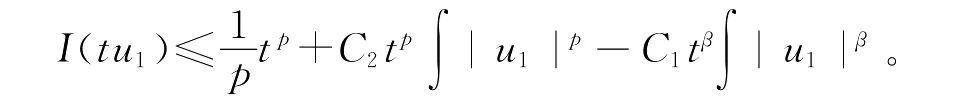
注意到β＞p，故当t＞ρ充分大，取u0＝tu1，则必有且

至此，由引理1～5完成了定理1的证明。

注2 （1）由上述证明过程可以看出所得到的非平凡解u是部分径向的，即当时，必有

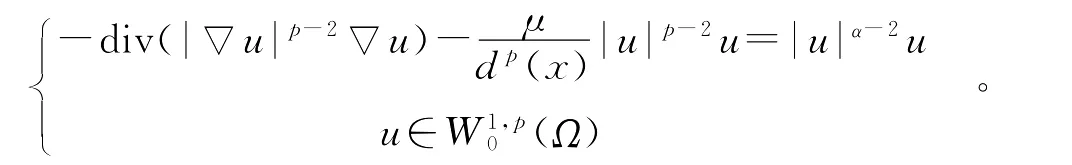
［1］ Ian Schindler.Quasilinear elliptic boundary－value problems on unbounded Cylinders and a related mountain－pass lemma［J］.Arch Rational Mech Anan，1992，120：363－374.

［2］ P L Lions.The concentration－compactness principle in the calculus of variations，The locally compact case［J］.Ann Inst Herni Poincare Analyse Non Lineaire，1984，1：109－145；223－283.

［3］ Fan xianling，Zhao yuanzhang.Linking and multiplicity results for the p－Laplacian on unbounded cylinders［J］.J Math Anal Appli，2001，260：479－489.

［4］ Raghavenadra V，Sreenadh K.Nontrivial solutions for perturbations of a Hardy－Sobolev operator on unbounded domain［J］.J Math Anal Appli，2003，288：314－325.

［5］ 宣本金.变分法－理论与应用［M］.合肥：中国科学技术大学出版社，2006.

［6］ Michel Willem.Minimax theorems.Progress in nonlinear differential equations and their application［M］.Boston：Birkhauser，1996.

［7］ Lions P L.Symetrie et compacite dans les espaces de Sobolev［J］.J Funcl Anal，1982，49：315－334.

［8］ Richard S Palais.The principle of symmetric criticality［J］.Commun Math Phys，1979，69：19－30.

［9］ 张恭庆.临界点理论及其应用［M］.上海：上海科学技术出版社，1986.

［10］ Adams R A.Sobolev空间［M］.叶其孝译.北京：人民教育出版社，1981.

［11］ Lao Senyu.Nonlinear p–Laplacian problems on unbounded domains［J］.Proceedings of American Mathematical Society，1992，115：1037－1045.

The Existence of Solutions for a Class of p－Laplacian with Hardy－Sobolev Operator

ZHAO Yuan－Zhang1，YAN Xian－Wei1，ZHANG Qiang2
（1.School of Mathematical Science，Ocean University of China，Qingdao 266100，China；2.Weifang College of Science and Technology，Weifang 261000，China）

In this paper，with the principle of symmetric criticality，the existence of nontrivial solutions is proved for a class of p－Laplace equations with Hardy－Sobolev operator on unbounded cylinders.

p－Laplace equation；mountain pass lemma；principle of symmetric criticality

O175.25

A

1672－5174（2011）11－124－03

国家自然科学基金项目（10671169）资助

2010－11－17；

2011－04－29

赵元章（1972－），男，副教授。E－mail：zhaoyzh＠yahoo.com.cn

AMS Subject Classification：35J70

责任编辑 朱宝象