操作思维的项目差异及类属理论建构
刘改成
●专题研究
操作思维的项目差异及类属理论建构
刘改成
为考察不同运动项目操作思维的类属差异,以新研发的《BTL-SW-V1.2操作思维测试软件》对来自不同项群共10个项目的304名高水平运动员进行测试。研究显示,所测10个运动项目,具有显著操作思维类属差异。根据操作思维能力的高低,构建运动项目的操作思维类属理论,其中,乒乓球、羽毛球、曲棍球和跆拳道为一类,称之为高操作思维类;赛艇、游泳、体操、武术(套路)、射击(步枪)和举重为一类,称之为低操作思维类,前一类显著优于后一类,即操作步数少、操作反应快且操作思维学习能力强。
操作思维;项目差异;操作思维Vincent学习曲线;操作思维学习递进系数
在高水平运动竞技之中,认知能力尤其是思维能力对于运动员的运动绩效起着举足轻重的作用。在体育运动中,操作思维是运动员思维的主要表现形式[1],被认为在运动员认知特征的评定中,具有更好地预测效度。早期,“三筹码”试验是操作思维的主要研究范式[2],但在其指导下的研究并未发现操作思维与竞技能力之间具有规律性的正比关系[3-4]。
对此,梁承谋指出,以往研究的“三筹码”试验中的各种具体思维活动,因为没有严格的时间限制,被试可充分思考后再进行动作操作,其实质是变相的逻辑思维结果,未能真正反映操作思维的本质,不是运动专家所期望的操作思维意义。运动员生活环境特殊,其所面对的需要解决的问题特性,以及问题解决的方式上具有特殊性,表现为:加工智源狭窄、难以逻辑推理、难以表象加工、必须快速决策。这些特征说明,操作思维既不是形象思维,又不是逻辑思维,更不是儿童似的动作思维,其只能是一种直觉性思维,“直觉性”是其本质属性。借鉴认知心理学理论,直觉的操作定义被界定为:在2 s以内,对多于1比特信息量进行加工的复杂判断活动,并且判断结果的正确性明显高于随机判断概率或普通人的基线判断概率[5-6]。
结合“直觉性”这一特征,研究者在羽毛球等多项运动中开展了操作思维的研究[7-10]。研究验证了操作思维“直觉性”的存在,并且显示,操作思维具有很好的预测效度,能够有效区分不同水平的运动员。但已有的研究数量不多,且大多是单个运动情境下的、纵向研究,难以进行有效地比较和推广。因此,研究者认为,考察不同项目之间的操作思维能力是当前亟待解决的问题。而进行项目间横向比较的高级研究思路,是对项目进行类属的探讨[11],以从宏观的高度对运动项目在某一指标上的特性进行理论思辨、概括和总结,以获得其本质规律,进行广泛的应用和推广。
为此,研究者新开发了BTL-SW-V1.2操作思维测试软件[12],选择了教育心理学中进行动作思维测试最常见的“河内塔”为测试内容,在计算机上进行测试试验,与以往“三筹码”试验相比,该软件具有3个明显特点:(1)用计算机程序实现测试过程,计算机自动记录操作步数、持续时间等,解决记录精度问题;(2)限制每步的操作时间不超过2 s,确保被试进行“直觉”的快速思维决策;(3)引入文森特曲线统计法,控制“熟练程度”因素,从学习进程的角度探讨操作思维与竞技能力的关系。
1 研究对象与方法
1.1 被 试
被试为15个省市专业队及6个北京体育大学竞技体院专业队的部分运动员。运动水平为国家一级及以上。来自体操、武术(套路)、游泳、羽毛球、举重、乒乓球、曲棍球、赛艇、射击(步枪)和跆拳道10个项目。其中有效被试304名,男156人(平均年龄19.42+2.65,平均训练年限8.11+3.75);女148人(平均年龄19.86+3.43,平均训练年限8.31+3.51)。
1.2 试验方法
1.2.1 操作思维测试软件的信度 BTL-SW-V1.2操作思维测试软件的信度检验采取了重复测量法。通过对北京体育大学竞技体院羽毛球专业的16名运动员(男8,女8)进行初测和再测(2个月之后),其检验结果见表1。

注:r为重测相关系数,*P<0.05。
由表1可知,本测试系统的重测系数均高于推荐值0.70,本测试结果是值得信赖的。
1.2.2 试验程序 试验要求在安静、舒适的环境中进行,仅有主试和被试在场。安装《BTL-SW-V1.2操作思维测试》软件,在电脑上进行河内塔搬运测验。受试者坐于显示屏前约25~35 cm,用鼠标操纵整个测试过程,电脑自动记录测试过程的所有参数。测试内容包括初级、标准、附加3种测试程序。正式测试前必须先使用初级程序进行练习,以使被试明确测试要求,熟悉测试环境和熟练掌握操作方法。具体程序如下:(1)开始测试前,主试首先讲解测试目的、要求、规则。(2)进入练习界面后,主试结合测试指导语讲解测试要求和操作方法。(3)讲解后,观察被试练习过程。被试至少练习3遍以上(多则不限),直到已熟练掌握鼠标操作方法为止。练习为3盘3柱搬运程序。(4)点击正式测试按钮开始正式测试。标准测试为:5盘3柱搬运程序,其中每步时间由电脑程序严格控制在2 s以内。(5)检查测试结果。
1.3 试验设计
采用运动项目(10)×性别(2)的组间设计。运动项目和性别为组间变量。同时为了考察年龄对运动员操作思维能力的影响效果,将其作为协变量纳入模型。因变量包括操作错误步数、操作反应总时间(s)以及操作思维Vincent学习十等分阶段的操作用时(s)。
1.4 统计处理
采用Excel 2003和SPSS 11.5软件对数据进行统计处理。通过层次聚类分析(Hierarchical cluster analysis)考察运动项目的操作思维类别属性;采用一般线性模型中的多元协方差分析(Analysis of Multiple Covariance)考察自变量对因变量的主效应及自变量之间的交互作用,其中年龄为协变量。
2 结果与分析
2.1 10个运动项目的操作思维聚类分析结果
以每个项目的操作错误步数、操作反应总时间的均值作为变量值,以运动项目作为样品,进行层次聚类(Hierarchical Cluster)分析(见表2)。

表2 10运动项目操作错误步数和操作反应总时间的平均数和标准差Tab.2 Means and Standard Deviations for Operational Thinking Error Steps and Reaction Time of Athletes among 10 Sports Events(n=304)运动项目 人数 操作错误步数 操作反应总时间/s曲棍球 27 34.93±21.86 53.14±19.06羽毛球 25 35.36±21.01 54.18±23.31乒乓球 25 37.44±20.93 51.45±13.14跆拳道 32 39.44±24.61 55.24±20.76射击 36 58.25±52.54 73.16±48.00武术 30 61.67±44.50 73.41±35.65举重 30 62.80±42.11 76.37±35.08体操 30 63.67±50.82 76.33±42.04赛艇 36 64.31±35.84 75.12±30.64游泳 33 68.70±56.02 73.53±39.09
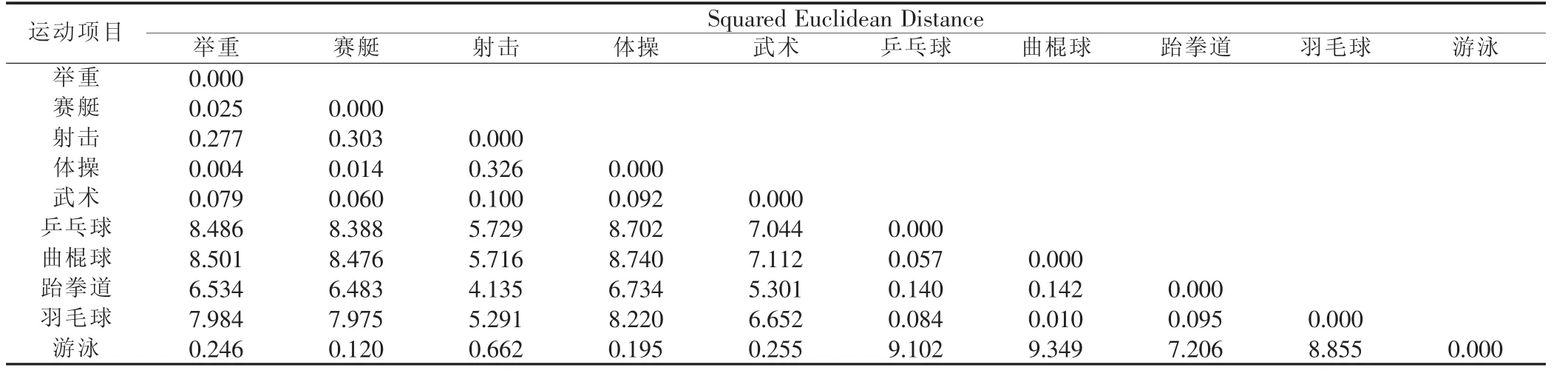
表3 欧氏平方距离矩阵Tab.3 Proximity Matrix
根据假设,研究者将分类个数定为4、3和2分别进行了探索,见表3、表4和图1。分为4类不太合理,难以在聚类树形图上得到有效体现,并且欧氏平方矩阵系数也显示,羽毛球、乒乓球、跆拳道和曲棍球项目明显成为一类;举重、体操、武术、赛艇、游泳彼此之间的关系也非常密切,自成一类;射击与羽毛球、乒乓球、跆拳道和曲棍球之间的距离较远,而相较于举重、体操、武术、赛艇和游泳,也稍有一定的距离,根据聚类树形图,可将其单独归为一类,也可将其归为举重等项目中,即根据聚类分析结果,初步可将10个运动项目划分为2类或3类。

表4 运动项目分为2、3、4类时的聚类结果Tab.4 Cluster Membership
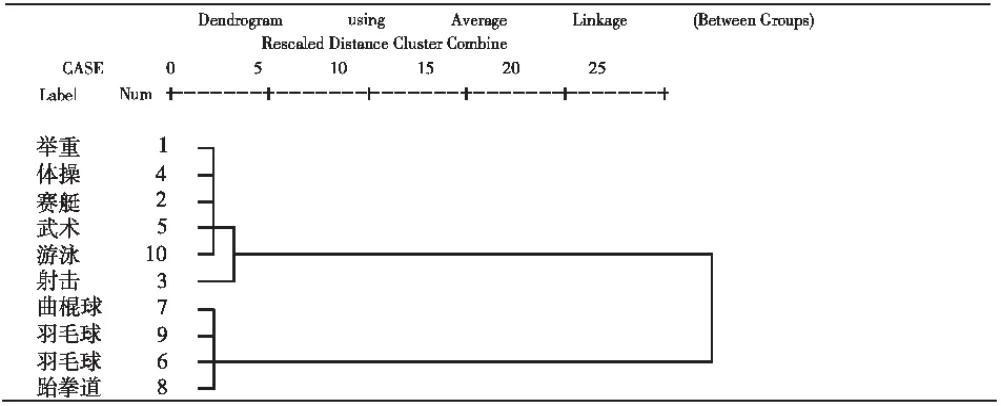
图1 聚类树形图Fig.1 Dendrogram
为了进一步检验聚类的科学性与否,我们按照3类与2类的划分分别进行了差异性检验,将其归为3类,方差分析结果显示,无论在操作错误步数还是操作反应总时间上,以射击项目为主的这一类别与其他两个类别之间的差异均没有达到显著性水平(分别为P=0.846,P=0.073;P=0.987,P=0.071);将其归为2类,T检验结果显示,在操作错误步数和操作反应总时间两项指标上,两组之间的差异均达到极其显著水平(t=6.612,P=0.000,ES=0.091;t=6.333,P=0.000,ES=0.086)。
据此,根据运动员的操作思维能力,研究者将10个运动项目划分为两类:第一类(I类):羽毛球、乒乓球、跆拳道和曲棍球;第二类(II类):举重、体操、武术(套路)、赛艇、游泳和射击(步枪)。
2.2 运动项目的操作思维类属差异检验结果
2.2.1 I类和II类项目运动员操作错误步数和操作反应总时间的比较 以年龄为协变量,考察运动项目、性别对两个直接观测变量——操作错误步数和操作反应总时间的影响,多元协方差分析结果显示,运动项目主效应显著(Pillai's Trace F=1.921,P= 0.012),性别主效应不显著(Pillai's Trace F=1.719,P=0.181),运动项目和性别交互效应不显著(Pillai's Trace F=1.921,P= 0.948),协变量年龄主效应不显著(Pillai's Trace F=1.623,P= 0.199)。因为协变量年龄与因变量之间的线性相关未达到显著水平,去掉年龄后,多元方差分析结果(见表5)。


注:*P<0.05,**P<0.01(下同)。
由表6可知,在两个因变量上,运动项目主效应均达到显著水平,而性别、及运动项目和性别的交互作用均不显著。不同项目间差异的多重比较结果(LSD)显示,在操作错误步数上,Ⅰ类4项目彼此之间差异不显著(P>0.05);Ⅱ类6项目彼此之间差异也不显著(P>0.05)。Ⅰ类与Ⅱ类运动项目之间差异的比较结果显示,Ⅰ类4项目与Ⅱ类举重、赛艇、武术、体操和游泳等5项目之间彼此两两差异达到显著水平,而Ⅱ类射击除与Ⅰ类的曲棍球之间的差异达到显著之外(P<0.05),与其他8个项目之间的差异均未达到显著水平(P>0.05)。在操作反应总时间上,Ⅰ类4项目彼此两两之间的差异不显著(P>0.05);Ⅱ类6项目彼此两两之间差异不显著(P>0.05);I类4项目中任一项目与Ⅱ类6项目中任一项目两两之间差异均达到显著水平。
总之,在操作错误步数和操作反应总时间上,Ⅰ类项目运动员显著优于Ⅱ类项目运动员,即Ⅰ类项目运动员操作错误步数更少、操作反应更快。
2.2.2 Ⅰ类和Ⅱ类项目运动员的操作思维Vincent学习曲线特点比较 河内塔搬运任务需要多步运作,方能完成。因搬运原则一样,后面操作均以前面为借鉴,这就产生了明显的学习问题,搬运所用步数少,耗时短,则说明操作学习快。Vincent曲线是心理学研究中使用的一种特殊学习曲线,它运用独特的表达方法,显示不同学习阶段的不同学习效果:即把每个被试者的学习全过程分成十等分,然后把每个被试者相应学习阶段的学习效果加以平均,这样就能如实反映所有被试在各个学习阶段的学习状况[12-13]。本文将整个操作任务完成过程分成十等分,从而计算各等分所需的操作时间,并绘制Vincent学习曲线,据此定性分析运动员操作思维学习的内部进程特点。两类项目运动员操作思维Vincent学习曲线特点比较如下。
(1)操作思维学习十等分阶段的操作用时。
以各项目在十等分阶段上的平均用时为纵坐标,I类和II类的10个项目十等分阶段的Vincent曲线见图2。总的来看,I类项目几乎在每一等分阶段,其操作用时均低于II类项目。
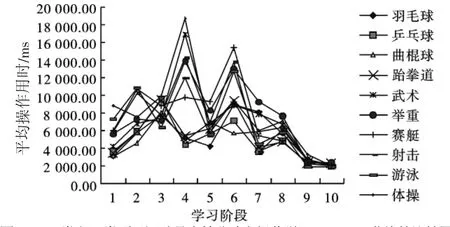
图2 I类和II类项目运动员十等分阶段操作学习Vincent曲线的比较图Fig.2 Comparison of the Vincent Learning Curve of Operational Thinking between I and II Sports Events Categories
以年龄为协变量,考察运动项目、性别对运动员操作思维学习十等分阶段操作用时的影响,多元协方差分析结果显示:运动项目主效应显著(Pillai's TraceF=1.597,P=0.000),性别主效应显著(Pillai's TraceF=3.112,P=0.001),协变量年龄主效应不显著(Pillai's TraceF=0.761,P=0.667),运动项目和性别的交互作用不显著(Pillai's TraceF=0.905,P=0.727)。
去掉年龄后,多元方差分析结果显示,运动项目之间的差异主要存在于第1等分阶段(Pillai's TraceF=2.558,P=0.008)、第4等分阶段(Pillai's TraceF=3.037,P=0.002)、第 6等分阶段(Pillai's TraceF=2.369,P=0.014)、第7等分阶段(Pillai's TraceF=2.110,P=0.029)和第9等分阶段(Pillai's TraceF=2.592,P= 0.007)。性别之间的差异主要表现在第1等分阶段(Pillai's TraceF=8.526,P=0.004)和第10等分阶段(Pillai's TraceF= 6.455,P=0.012)。
不同项目间差异的多重比较结果(LSD)显示,总的来看,在操作思维学习十等分阶段的操作用时上,差异主要体现在I类4项目和II类6项目之间。Ⅰ类项目运动员的操作思维学习十等分阶段操作用时显著优于Ⅱ类项目运动员。
(2)操作思维Vincent学习曲线类型。
在总体坐标图上,根据运动员操作思维Vincent学习曲线的峰值、走向,可将304名运动员的操作思维Vincent学习曲线划分为6种类型[14](见表7)。
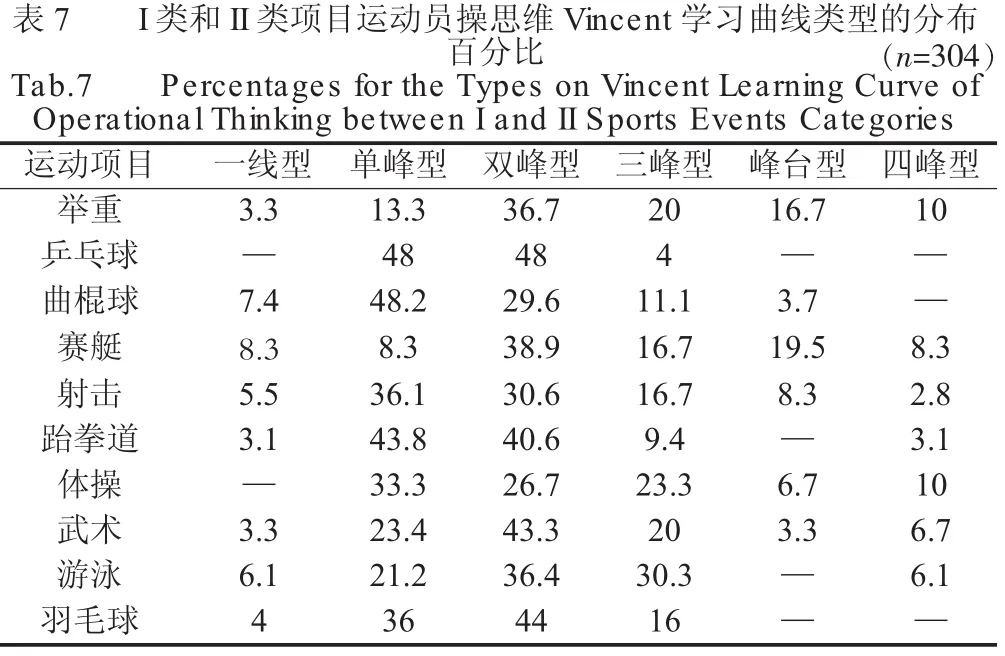
表7 I类和II类项目运动员操思维Vincent学习曲线类型的分布百分比Tab.7 Percentages for the Types on Vincent Learning Curve of Operational Thinking between I and II Sports Events Categories(n=304)运动项目 一线型 单峰型 双峰型 三峰型 峰台型 四峰型举重 3.3 13.3 36.7 20 16.7 10乒乓球 — 48 48 4 — —曲棍球 7.4 48.2 29.6 11.1 3.7 —赛艇 8.3 8.3 38.9 16.7 19.5 8.3射击 5.5 36.1 30.6 16.7 8.3 2.8跆拳道 3.1 43.8 40.6 9.4 — 3.1体操 — 33.3 26.7 23.3 6.7 10武术 3.3 23.4 43.3 20 3.3 6.7游泳 6.1 21.2 36.4 30.3 — 6.1羽毛球 4 36 44 16 — —
(3)操作思维学习的递进系数。
为了对操作思维学习进程进行定量的分析说明,本研究引入了递进系数(Dj)来比较运动员操作学习进步幅度的高低[15]。其中,运动员在每一等分阶段的操作用时为变量值。所谓递进系数是指每一运动员从一个学习阶段到另一个学习阶段的学习进步率(递减率),其公式为:Dj=(Y-X)/Y。通过平均递进系数来反映每一运动员的操作学习进步幅度,运动员的平均递进系数公式为:
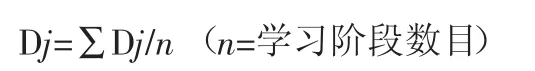
如图3所示,I类4项目其操作思维学习递进系数大于或等于-0.5,而II类6项目均小于-0.5,总的来看,I类项目操作思维学习递进系数大于II类项目。

图3 I类和II类项目运动员操作思维学习平均递进系数的比较图Fig.3 Comparison of the Progressive Coefficient of Operational Thinking Learning between I and II Sports Events Categories
以年龄为协变量,考察运动项目、性别对操作思维学习递进系数的影响,一元协方差分析结果显示,运动项目主效应显著(F=2.380,P=0.013),年龄主效应不显著(F=0.942,P=0.333),性别主效应不显著(F=2.611,P=0.107),运动项目与性别交互作用不显著(F=1.852,P=0.059)。去掉年龄后,一元方差分析结果见表8。
如表8所示,运动项目主效应达到显著水平,而性别主效应,运动项目与性别的交互效应均未达到显著水平。不同项目间差异的多重比较结果显示(LSD),在操作思维学习递进系数上,I类4项目与II类赛艇、举重、武术、体操和游泳5项目之间,两两之间的差异均达到显著水平。而II类射击与其他项目之间的差异均未达到显著。

表8 I类和II类项目、不同性别运动员操作思维学习递进系数的方差分析Tab.8 Analysis of Multiple Covariance for the Effects on Sports Events and Gender Affecting the Progressive Coefficient of Operational Thinking Learning(n=304)变异源 均方和 自由度 均方 F Sig. 效果量运动项目 23.150 9 2.572 2.587 0.007** 0.076性别 3.024 1 3.024 3.041 0.082 0.011运动项目*性别 15.948 9 1.772 1.782 0.071 0.053误差项 282.383 284 0.994
总之,在操作思维学习递进系数上,I类项目显著优于II类项目运动员,其操作思维学习进步幅度更大。
3 分析与讨论
聚类结果显示,根据操作思维特性,可以将10个运动项目划分为两类:I类包括乒乓球、曲棍球、跆拳道和羽毛球4个项目,II类包括武术(套路)、射击(步枪)、游泳、赛艇、体操和举重6个项目。这种类别的划分符合我们对运动项目的观察,符合人们对运动项目的常规认识。
而进一步分析显示,无论是从操作错误步数、操作反应总时间还是操作思维Vincent学习曲线的变化特点上都证明I类和II类运动项目是两个不同的类别。I类项目运动员其操作思维能力显著高于II类项目运动员,即操作步数少、操作反应快且操作学习能力强。研究结果基本支持了研究假设,即“运动项目具有操作思维的类属差异”。
3.1 两类项目的行为特征差异
3.1.1 竞技对抗性程度不同 I类4项目同属技能主导类同场对抗项目[14],存在攻防对抗,而II类6项目则属于非对抗性项目。I类4项目的运动情境表现出如下特点:(1)攻防转换次数多,对抗频率高,其运动行为具有一定的连续性。运动员需要连续对对手的行为进行分析预测,运动决策的频率高。(2)攻防转换的速度快,对抗激烈,运动中存在很强的时间压力。如乒乓球运动中,在连续的击球过程中,从对手击球开始到本方挥拍迎球,运动员往往只有0.3~0.6 s的时间对对手的行为作出判断[9],运动决策的时间紧迫。而时间决定着运动决策的类型[16]。
3.1.2 动作结构的复杂性不同 动作结构是引发运动决策的直接和主要的刺激元素。I类4项目、II类体操和武术等同属多元动作结构,而II类其他4项目则属于周期性或非周期性单一动作结构。单一动作结构的项目技术动作简单,种类少,如射击技术主要包括据枪、瞄准和击发3个环节。而多元动作结构的项目,技术动作变化多样,如自由体操由跳跃、空翻和转体等多项技术构成,乒乓球则包括推、搓、攻等8大类81项技术动作。但是,对同属多元动作结构的6个项目进行仔细分析发现,I类4项目由于存在攻守对抗,受到对手的影响,因此,其动作结构组合具有变异性,需要根据比赛情况或对手情况的变化而变化。以乒乓球为例,将弧线、力量、速度和运行路线等按实战情况粗略分档,可以形成将近1 400万种组合技战术[9]。而II类武术和体操尽管也属于多元动作结构组合,但其属于多元动作结构的固定组合,运动员只需要在赛场上完整“再现”千百次重复练习的动作组合即可,运动情境相对固定。
3.1.3 环境的开放性程度不同[17]I类4项目都属于典型开放式技能项目。运动员所处的环境复杂,其运动行为受到对手、同伴(曲棍球)、场地、器材和观众等多方面因素影响。其中,由于存在攻守对抗,运动员最主要受到竞赛对手的影响,运动员需要准确预测对手的动向,及时根据对手变化确定和实施动作方式。而II类6项目则属于闭锁式技能运动项目,其受器材、场地的影响不大,运动员主要依靠内部本体感受器所介入的反馈来进行调节,很少根据对手的情况进行直接、迅速和反复的调节。
总的来看,在I类开放式技能项目中,运动情境复杂多变,技战术种类多,变化多,甚至存在一定的虚假性和欺骗性。在竞技双方制约与反制约的较量中,运动员为了争取自己主动,必须作出适宜的行为选择,而前提,是对对手的行为作出准确预测,因此,在I类项目的竞技过程中,存在着复杂的思维判断活动。另外,由于攻守矛盾突出,攻防转换快且频率高,运动员面临着极大的时间压力,要求其必须快速、连续作出决策判断,其运动决策具有极大的不确定性和或然性。相对而言,II类项目属于闭锁式运动技能项目,运动员主要靠内部本体感受器所介入的反馈进行内部调节,受外界影响很少,强调以“我”为主,强调“求同”,运动情境简单、固定,因此,运动情境中对思维的要求相对不高。
3.2 两类项目的操作思维特征差异
研究发现,在操作决策速度、操作决策正确性和操作决策认知复杂性等思维特性上,I类与II类项目有明显不同。
在操作反应总时间上,I类项目运动员显著优于II类项目运动员,说明,操作反应总时间是一个很敏感的指标。操作反应总时间反映了运动员决策判断的速度。决策速度越快,说明运动员的操作决策水平越高。I类项目运动员的操作决策水平优于II类项目的运动员。
在操作错误步数上,除II类射击项目外,I类4项目显著优于II类其他5项目。研究结果提示:(1)相较于操作反应总时间,操作错误步数对于区分运动项目而言可能不是一个敏感的指标;(2)可能存在速度-准确性的权衡,射击运动员为了追求决策准确性而牺牲了一定的决策速度;(3)同一类别内部,不同项目的操作思维特性会存在需求的不同,后续的运动项目操作思维类属研究需要予以关注。但总的来看,I类项目运动员的操作错误步数优于II类项目运动员。操作错误步数实际上是运动决策的错误判断次数,操作错误步数越多,表明错误决策越多,说明运动决策的水平较低。I类项目运动员运动决策的水平高于II类项目运动员。
此外,研究者从运动员操作思维Vincent学习曲线的特点上对两类项目运动员操作思维内部学习进程的特点进行了分析。
在总体坐标图上,304名被试的操作思维Vincent学习曲线被划分成为6类[14]:一线型,被试的学习曲线波动很小,近似于一条直线,运动员操作思维学习能力优异,几乎没有犯错误;单峰型,有一个波峰出现,从学习进程来看,在犯了一次错误之后能够迅速的予以改正,运动员操作思维学习能力良好;双峰型,学习曲线出现了两个波峰,从学习过程来看,在第一次出现操作错误之后,又再次出现错误,在两次错误之后才能予以改正,运动员的操作思维学习能力一般;三峰型和四峰型,学习曲线来看出现了3个或4个波峰,从学习过程来看,在出现了两次大错误之后,运动员仍然没有予以改正,又犯第3次、第4次错误,说明运动员的操作思维学习能力较差;峰台型,运动员在学习过程中连续出现相同的错误,学习过程中出现了一个停滞期,说明运动员操作学习能力较差,其是双峰型、三峰型和四峰型等学习曲线类型的特例。
研究结果显示,Ⅰ类4项目各包含近40%以上的一线型和单峰型运动员,而除射击外,Ⅱ类其他5项目则各包括了近40%及以上的三峰型和四峰型运动员,比较而言,Ⅰ类4项目运动员犯错误的比例更少,操作思维学习能力相对较强。
对两类项目运动员总体操作思维Vincent学习曲线的波形、峰值和走向的进一步分析显示,相较于Ⅱ类6项目,Ⅰ类4项目运动员的操作思维学习曲线更平坦、波峰更少、波峰值更小。从波峰分布位置和具体的波形走向来看,Ⅰ类项目运动员的操作思维Vincent学习曲线的波峰主要分布于第3、第6和第8等分阶段,操作思维学习曲线呈现前高后低之走势,说明在操作学习的前半阶段犯了一次大错之后,能够吸取教训,减少错误的次数;而Ⅱ类6项目运动员的操作思维学习曲线的波峰主要分布于第2、第4、第6和第8等分阶段,其操作思维学习曲线跌宕起伏,呈前低后高之势,说明,运动员在操作学习的前半阶段连续犯两次大错误之后,仍没有吸取教训,在后半阶段又连续出错,说明运动员的操作思维学习能力较差。
根据操作思维Vincent学习曲线的划分标准,其十等分阶段,每一阶段的目的任务不同,从对整体问题解决的重要性来看,第1、3、5、6和8等分阶段是问题解决的关键阶段[18]。研究结果显示,Ⅰ类4项目运动员在第3等分阶段用时最长,但仍然低于Ⅱ类运动项目运动员,在第6和第8等分阶段有一定的耗时,但相对而言用时较少,并且显著低于Ⅱ类项目运动员,反映运动员对早期关键问题具有更好的把握能力,并且显示了很好的问题解决策略;而Ⅱ类项目运动员在第1、第4、第5、第7和第9等分阶段上都显示出了更多的操作用时,并显著高于Ⅰ类项目运动员,结合波峰的分布状况,可以看出,运动员是均衡用力,对于问题的复杂性认识不足,从一开始就犯错误,思维混乱,对于早期问题的关键阶段没有很好的把握,几乎没有问题解决策略的参与。
总之,由以上定性分析的结果可知,Ⅰ类项目运动员不同于Ⅱ类项目运动员,显示出更好的对复杂问题的认知能力。
此外,研究者引入了递进系数的计算方法对操作思维Vincent学习曲线进行定量评估,考察运动员的操作思维学习进步幅度。结果显示,两类项目运动员的操作思维学习递进系数取值范围不同,I类4项目运动员在-0.5~0之间,而Ⅱ类6项目运动员则在-0.87~-1.16之间,除Ⅱ类射击项目外,Ⅰ类项目运动员均显著优于Ⅱ类项目运动员。此结果提示,操作思维学习递进系数是一个较好的反映运动员操作思维内部信息加工能力的一个定量指标,能够有效的对不同项目的运动员进行区分,-0.5可能是两类项目运动员操作思维学习能力的一个有效的界限,小于它,则操作思维学习能力较差,大于它,则操作思维学习能力较强,不过尚需要后续研究的进一步证实。
3.3 运动项目的操作思维类属理论建构
综上,I类与II类运动项目具有明显的不同,I类项目运动员的操作思维能力优于II类项目运动员。根据两类项目运动员操作决策过程中的思维特性,我们将I类项目称之为“高操作思维类”,而II类项目称之为“低操作思维类”。10个运动项目的操作思维类属理论模型见图4。
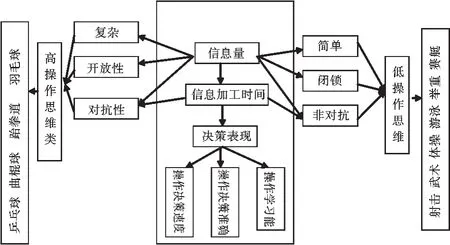
图4 10个运动项目操作思维类属理论建构图Fig.4 Construction of the Classification Theory on Operational Thinking among 10 Sports Events
在此基础上,通过归纳与总结,研究者对高操作思维类项目和低操作思维类项目进行了初步的界定:
高操作思维类:在典型开放式技能的运动情境下,运动员的决策受到对手或外界环境等复杂因素的极大制约,在激烈的时间压力下,运动员往往需要利用有限的信息去作出快速、直接或或然的决策,要求有较高的信息加工水平或较优的问题解决策略的参与。
低操作思维类:在闭锁式技能的运动情境下,运动情境相对简单、稳定,在竞技过程中,思维参与的成分很少,运动员的决策水平较低,对复杂问题的认知能力较低。
4结 论
(1)根据所测操作错误步数、反应时间等指标,构建运动项目的操作思维类属理论,将十个运动项目中的乒乓球、曲棍球、跆拳道和羽毛球归为一类,称之为高操作思维类;将射击、武术、体操、赛艇、游泳和举重归为另一类,称之为低操作思维类。前一类显著优于后一类,即操作步数少、操作反应快且操作思维学习能力强。
(2)操作思维学习递进系数(Dj)是运动项目操作思维类属理论的数值区分点,Dj大于-0.5,是高操作思维类,小于-0.5,是低操作思维类。
(3)操作思维Vincent学习曲线较好的反映了运动员操作思维学习进程中质的变化特点。在总体坐标图上,根据其峰值、走向,可将304名运动员的操作思维学习曲线划分为6类:一线型、单峰型、双峰型、三峰型、四峰型和峰台型。
[1]鲁吉克.运动心理学[M].汤秉南,译.武汉:武汉体育学院科研处,1979:75.
[2]罗季奥昂诺夫.运动能力的心理学诊断[M].卢振南,译.武汉:武汉体育学院科研处,1984:26.
[3]周百之.乒乓球运动员的操作思维[J].中国体育科技,1984(17):3-5.
[4]邱宜均,贝恩渤.甲级排球运动员操作思维的初步研究[J].心理学报,1984(5):31-37.
[5]韩晨.问题情境及技术等级对运动员直觉性思维的影响:对棒球运动员投一击球判断准确性和时间的试验 [D].北京:北京体育大学,2000.
[6]刘改成,梁承谋,程勇民.操作思维理论内涵的重新诠释与证实[J].首都体育学院学报,2008,5(20):101-103.
[7]漆昌柱.羽毛球专家-新手在模拟比赛情境中的问题表征与运动思维特征[D].北京:北京体育大学,2001.
[8]王斌.女子手球运动员模拟运动情境中认识决策与直觉决策的实验研究[J].上海体育学院学报,2003,27(2):23-27.
[9]李今亮.乒乓球运动员接发球判断的思维活动特征[D].北京:北京体育大学,2005.
[10]王长生.不同逻辑背景下跆拳道运动员直觉判断速度及决策准确性研究[D].北京:北京体育大学,2007.
[11]田麦久,刘筱英.论竞技运动项目的分类 [J].北京体育大学学报,1983,11:41-46.
[12]梁承谋,程勇民,付全,等.BTL-SW-V1.2操作思维测试系统的开发与检验[J].体育学刊,2007,6:34-36.
[13]孟庆茂,常建华.试验心理学[M].北京:北京师范大学出版社,1999:292-293.
[14]梁承谋,刘改成,王长生,等.羽毛球运动员操作性思维文森特(Vincent)学习曲线类型特点初探——62名运动员BTL-SW-V1.2操作思维软件测定图形分析 [C]//第八届全国运动心理学大会论文汇编.武汉:武汉体育学院,2006:124-125.
[15]谢亚龙,王汝英,王清.体能类项群运动成绩的中长期预测方法-递进系数法的研究[J].体育科学,1990,5:37-40.
[16]Hubert Ripoll.The understanding acting process in sport:the relationship between the semantic and sensorimotor visual function[J].International Journal of sport psychology,1991,22:221-243.
[17]张力为,毛志雄.运动心理学 [M].上海:华东师范大学出版社,2003:214.
[18]张小将.汉诺塔问题解决的认知过程分析[D].南京:南京师范大学,2004.
Events Differences of Operational Thinking and Construction of Its Classification Theory
LIU Gaicheng
(Section of PE,Guangzhou Medical University,Guangzhou 510182,China)
The operational thinking testing software of BTL-SW-V1.2,newly-published,was used as the research tool.The categorical differences of operational thinking between sport events were examined.304 elite athletes from 10 sports events were chosen as subjects.The main conclusion revealed the categorical differences of operational thinking between the sport events were significant.According to the abilities of operational thinking,10 sports events could be divided into two categories:one was called High Operational Thinking Strategy Event-group,including field hockey,table tennis,badminton and taekwondo;the other one was called Low Operational Thinking Strategy Event-group,including rowing,swimming,gymnastics,wushu(taolu),shooting(rifle)and weight-lifting.In which the former was better than the latter,that is to say,less steps,faster reaction time and higher learning ability.
operational thinking;events differences;Vincent learning curve of operational thinking;progressive coefficient of operational thinking learning
G 804.8
A
1005-0000(2011)04-0290-07
2011-02-26;
2011-05-09;录用日期:2011-05-15
刘改成(1972-),女,湖北襄樊人,博士,讲师,研究方向为运动心理学。
广州医学院体育教研室,广东广州 510182。
据此,依据“项群理论”[11],以及“奥运优势项目”优先原则,本文选择羽毛球、乒乓球、曲棍球、跆拳道、体操、射击、举重、赛艇、游泳和武术共10个项目,利用BTL-SW-V1.2操作思维测试软件进行测试,通过标准化的测验,从“直觉性”角度来考察其具有的操作思维类属差异。这与以往一般训练学中,关于运动员应具有的心智能品质的经验式描述具有实质的不同,也将填补无从心理学品质角度对项目进行类属划分的空白。
本研究假设:众多运动项目由于其动作规则的构成不同,应具有操作思维的类属差异。

