我国国债收益率的预测与评价

李龙泰，何树红

(1．四川建筑职业技术学院 经管系，四川 德阳 618000;2．云南大学 数统学院，云南 昆明 650091)

一、时间序列模型介绍

我们知道，金融上的随机序列一般都具有自相关性，可以用时间序列模型来进行模拟。收益率随时间变化，且在每个时间点上都只取一个观测值，收益率的波动变化可以看成时间序列过程。可以采用时间序列模型对利率进行建模，用于刻画收益率的波动性。时间序列分析法是伯克斯·詹金斯(Box·Jenkins)提出的。这种建模方法不考虑以经济理论为依据的解释变量的作用，而是依据变量本身的变化规律，利用外推机制描述时间序列的变化。建立时间序列模型的前提是时间序列必须具有平稳性，如果时间序列是非平稳的，建立模型之前应先把它变换为平稳的时间序列，同时仍保持原时间序列的随机性。建立时间序列模型主要包括三个步骤:第一，时间序列的识别及模型形式的选择;第二，模型参数的估计;第三，模型的诊断检验。这里我们采用 ARIMA［1］(P234)模型进行分析。

一般的ARMA(p，q)模型的形式为:

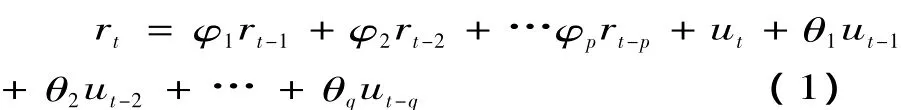
其中Φ(L)和Θ(L)分别表示L的p，q阶多项式，分别称为自回归算子和移动平

均算子。

由经验得知，收益率序列一般为非平稳的，而ARMA模型要求序列为平稳序列，因此需要将收益率序列进行1阶差分变为平稳序列，从而变成AR IMA模型。

我们已知AR和MA模型具有以下性质:

对于MA模型，ACF(自相关函数)是决定其阶数的有力工具，因为对MA(q)序列ACF是q阶后截尾的;对 AR模型，PACF(偏自相关函数)是决定其阶数的有力工具，因为AR(p)过程PACF是p阶后截尾的。

另外，在资本市场中，经常可以发现这样的现象:资产的向下运动通常伴随着比之程度更强的向下运动。为了解释这一现象，Engle和Ng绘制了好消息和坏消息的非对称信息曲线，认为资本市场中的冲击常常表现出一种非对称效应。这种非对称性是十分有用的，因为它允许波动率对市场下跌的反应比对市场上升的反应更加迅速，因此被称为“杠杆效应”，是许多金融资产的一个重要事实特征。而GARCH(1，1)模型认为收益的正方向变动和负方向变动对波动率变动幅度有着相同的影响，为了捕捉波动率变动的这一不对称性，我们引入TARCH(1，1)模型。这个模型中条件方差被定义为:

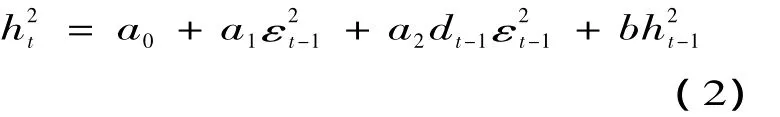
二、实证分析

样本分别选取Rm10的2006年2月27日到2008年12月12日的近600组数据，首先用Eviews5．0对Rm10的数据进行分析，由时间序列图我们可以看出，Rm10为非平稳序列。2006年至2007年1月之间收益率的波动幅度不大，但是2007年以后，收益率出现剧烈的波动，并在2007年12月达到最高点，2008年8月达到最低点。因此，也必须先对Rm10做1阶差分。由一阶差分知，Rm10的1阶差分序列平稳，可以对DRm10进行平稳性建模。

由DRm10的ACF和PACF都是4阶后截尾，可得ARIMA模型的方程为:

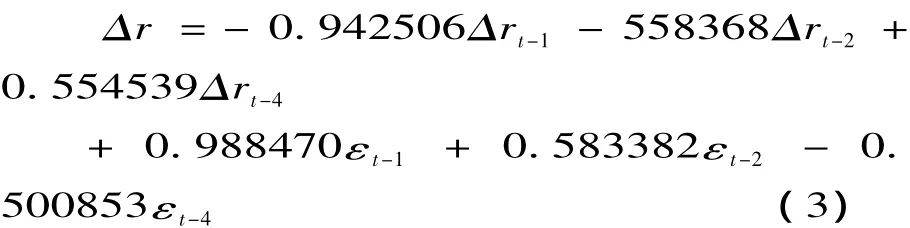
残差在表现出明显的异方差性的同时，还有波动集群性，因此有必要进行异方差检验，建立ARIMA模型为:

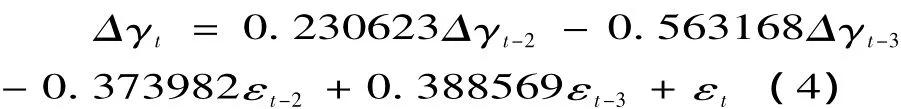
由Rm10的ARCH效应检验εt的12阶滞后的相伴概率仍然有p=0，拒绝原假设，残差序列存在高阶ARCH效应，即有GARCH 效 应， 因 次 对 残 差［2］(P24)进 行GARCH分析是必要的。由ARCH 1阶滞后的相伴系数的概率p=0．853691，接受原假设，残差序列的ARCH性已被消除。

模型估计结果较好，所有的系数均显著。β1，β4均小于零说明收益率的均值回复现象，与实际情况相符。α1＜ 0，φ ＞ 0，α1+θ1＜1都与GARCH模型的假设相符α1和θ1都显著不为零说明收益率的波动可有过去收益率的波动加以预测。α1+θ1＜1说明收益率波动具有有限方差属于弱平稳过程，波动最终会衰减。a1+θ1接近1说明交易所收益率对信息冲击反应是一个较慢的过程，冲击对交易所市场的影响具有持续性。

综上，交易所的国债收益率收益率波动方差具有有限方差均属于弱平稳过程，对信息冲击的反应较慢。

三、预测

预测的评价指标分别是(1)均方误差(RMSE)、(2)平均决对误差(MAE)、(3)平均绝对百分误差(MAPE)、(4)希尔不等系数(TIC)。上述四式中，t=s，s+1，s+2，…s+h。RMSE的平方叫均方误差，其对误差的微小变化十分敏感，在实践中也常用。上述指标前两项测量绝对误差，后两项测量相对误差。绝对误差比较直观，但取值大小受到量纲的影响，不能形成统一的评价标准。相对指标可以形成一致的评价标准，比如:MAPE的取值在0－5之间说明预测精度极高，在10以内说明预测精度高。TIC的取值范围是0－1之间，取值越小越好。

误差成分分析［3］(P245)指标分别是偏差率、方差率和协变率它们的取值范围都在0－1之间，三项指标之和等于1。它们的计算公式分别是:(1)偏差率、(2)方差率、(3)协变率。偏差率反映预测值和实际值序列的均值之差。如果偏差率很大说明预测是有偏的。方差率测量预测值序列和实际值序列标准差的差距，如果该指标取值较大，说明预测值与实际值的变异存在明显差异。这两项指标所反映的误差叫做系统误差，是预测中尽量要避免的。协变率所反映的误差是非系统误差或紊乱误差。一个理想的总误差中，系统误差应占的份额应尽可能的小，非系统误差所占的份额应尽可能的大，因此，偏差率和方差率应尽可能小，协变率应尽可能的大。

RM 10的预测结果如下:由图1知:MAP=2．643014 远小于 5，TC=0．015915接近0，说明预测精度极高，同时BP=0．400209，VP=0．002426，CP=0．597365，系统误差小于非系统误差，完全符合预测理论。综上，我们用 ARIMA－TARCH模型［4］(P145)分别对交易所国债收益率进行预测，效果良好。

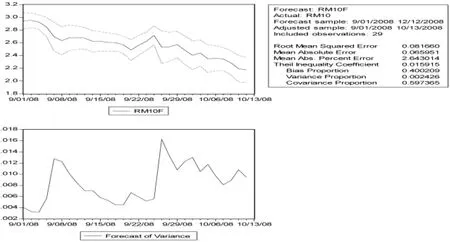
图1:RM10预测和方差

四、结论

本文在大量数据资料下，对我国国债收益率进行了定量和定性分析，用ARIMA－TARCH模型对交易所国债收益率进行预测，效果良好。国债市场是金融市场的基础，因而，对风险的防范和自身完善的要求更加紧迫。本文的分析还是比较粗浅，希望能采用极值理论结合 VaR［5］(P165)来分析极端事件对利率波动的影响情况，进而给出极端事件的风险度量。本文在很多地方还待完善和补充，希望以上文章能抛砖引玉，引起研究者的兴趣和思考。

［1］潘婉彬．银行间国债市场与交易所国债市场相关性研究［J］．数学与统计管理，2007，(3)．

［2］黄海南．GARCH类模型波动率预测评价［J］．中国管理科学，2007，(6)．

［3］鲁政委．基准利率体系完善与货币政策操作模式转变［J］．中国货币市场，2008，(7)．

［4］王晓亮．论完善我国国债市场［J］．当代经济(下半月)，2008，(9)．

［5］Mills·T·C．The Econometric modeling of Financial Time Serise［M］．Cambridge University Press，1979．